Vier-Farben-Satz

Beispiel einer Vier-Färbung

Der Vier-Farben-Satz (auch Vier-Farben-Theorem, früher auch als Vier-Farben-Vermutung oder Vier-Farben-Problem bekannt) ist ein mathematischer Satz und besagt, dass vier Farben immer ausreichen, um eine beliebige Landkarte in der euklidischen Ebene so einzufärben, dass keine zwei angrenzenden Länder die gleiche Farbe bekommen. Der Satz findet Anwendung in der Graphentheorie, Topologie und Kartografie.

Dies gilt unter den Einschränkungen, dass isolierte gemeinsame Punkte nicht als „Grenze“ zählen und jedes Land aus einer zusammenhängenden Fläche besteht, also keine Exklaven vorhanden sind.

Geschichte

4 Farben sind nötig

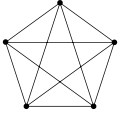
Der Satz wurde erstmals 1852 von Francis Guthrie als Vermutung aufgestellt, als er in einer Karte die Grafschaften von England färben wollte. Es war offensichtlich, dass drei Farben nicht ausreichten – siehe Abbildung rechts – und man fünf in keinem konstruierten Beispiel brauchte. In einem Brief des Londoner Mathematikprofessors Augustus De Morgan vom 23. Oktober 1852 an den irischen Kollegen William Rowan Hamilton wurde die Vermutung erstmals diskutiert und veröffentlicht: „Genügen vier oder weniger Farben, um die Länder einer Karte so zu färben, dass benachbarte Länder verschiedene Farben tragen?“.

Der englische Mathematiker Arthur Cayley stellte das Problem 1878 der mathematischen Gesellschaft Londons vor. Innerhalb nur eines Jahres fand Alfred Kempe einen scheinbaren Beweis für den Satz. Elf Jahre später, 1890, zeigte Percy Heawood, dass Kempes Beweisversuch fehlerhaft war. Ein zweiter fehlerhafter Beweisversuch, 1880 von Peter Guthrie Tait veröffentlicht, konnte ebenfalls elf Jahre lang nicht widerlegt werden. Erst 1891 zeigte Julius Petersen, dass auch Taits Ansatz nicht korrekt war. Heawood gab im Jahre 1890 mit der Widerlegung von Kempes „Vier-Farben-Beweis“ zusätzlich einen Beweis für den Fünf-Farben-Satz an, womit eine obere Grenze für die Färbung von planaren Graphen zum ersten Mal fehlerfrei bewiesen wurde. In Kempes fehlerhaftem Versuch steckten bereits grundlegende Ideen, die zum späteren Beweis durch Appel und Haken führten.

Heinrich Heesch entwickelte in den 1960er und 1970er Jahren einen ersten Entwurf eines Computerbeweises.

Dieser konnte von Kenneth Appel und Wolfgang Haken 1976 verbessert werden. Der Beweis reduzierte die Anzahl der problematischen Fälle von Unendlich auf 1936 (eine spätere Version sogar 1476), die durch einen Computer einzeln geprüft wurden.

1996 konnten Neil Robertson, Daniel Sanders, Paul Seymour und Robin Thomas einen modifizierten Computerbeweis finden, der die Fälle auf 633 reduzierte. Auch diese mussten per Computer geprüft werden.

2004 haben Benjamin Werner und Georges Gonthier einen formalen Beweis des Satzes in dem Beweisassistenten Coq konstruiert. Dadurch ist es nicht mehr nötig, den Computerprogrammen zur Überprüfung der Einzelfälle zu vertrauen, sondern „nur“ dem Coq-System.

Der Vier-Farben-Satz war das erste große mathematische Problem, das mit Hilfe von Computern gelöst wurde. Deshalb wurde der Beweis von einigen Mathematikern nicht anerkannt, da er nicht direkt durch einen Menschen nachvollzogen werden kann. Schließlich muss man sich auf die Korrektheit des Compilers und der Hardware verlassen. Auch der Mangel an mathematischer Eleganz des Beweises wurde kritisiert.

Fehlerhafte Gegenbeweise

• 

  Diese Karte wurde mit fünf Farben eingefärbt, und man muss …

• 

  … mindestens vier der zehn Regionen umfärben, um mit nur vier Farben auszukommen.

Wie viele offene Probleme der Mathematik hat der Vier-Farben-Satz eine Menge fehlerhafter Beweise und Gegenbeweise provoziert. Manche haben der öffentlichen Prüfung über Jahrzehnte standgehalten, bis sie als falsch erkannt wurden. Viele andere, hauptsächlich von Amateuren entwickelte, sind niemals veröffentlicht worden.

Häufig enthalten die einfachsten „Gegenbeispiele“ eine Region, welche alle anderen Regionen berührt. Dies erzwingt, um mit vier Farben auszukommen, die restlichen Regionen mit nur drei Farben auszufüllen. Da der Vier-Farben-Satz gilt, ist dies immer möglich. Die Person, die die Karte entwickelt, konzentriert sich aber häufig auf diese große Region und übersieht dabei schnell, dass es tatsächlich möglich ist.

Dieser Trick kann verallgemeinert werden; es ist leicht, Karten zu konstruieren, auf denen es unmöglich ist, mit vier Farben auszukommen, wenn die Farben einiger Regionen im Voraus festgelegt wurden. Ein oberflächlicher Überprüfer des Gegenbeispiels wird oft nicht daran denken, diese Regionen umzufärben, so dass das Gegenbeispiel gültig wirkt.

Andere falsche Gegenbeweise verletzen die Annahmen des Satzes in unerwarteter Weise, wie zum Beispiel durch Verwendung von Regionen, die aus mehreren, getrennten Bereichen bestehen, oder durch Verbieten von gleichfarbigen Regionen, die sich nur an einem Punkt berühren.

Formalisierung

Darstellung der Formulierung in der Graphentheorie

Formal lässt sich das Problem am einfachsten mit Hilfe der Graphentheorie beschreiben. Man fragt, ob die Knoten jedes planaren Graphen mit maximal vier Farben so gefärbt werden können, dass keine benachbarten Knoten die gleiche Farbe tragen. Oder kürzer: „Ist jeder planare Graph 4-färbbar?“ Dabei wird jedem Land der Karte genau ein Knoten zugewiesen; die Knoten angrenzender Länder werden miteinander verbunden.

Abwandlungen und Verallgemeinerungen

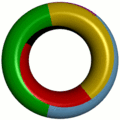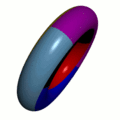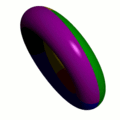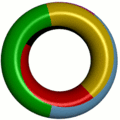
• Karte auf einem Torus, die sieben Farben benötigt
• 

  Karte mit 7-Färbung in der Ebene dargestellt

• 

  Animierter Torus derselben Karte

Das Vier-Farben-Problem ist ein Spezialfall der Heawood-Vermutung. Das klassische Vier-Farben-Problem betrifft Landkarten, die auf einer Ebene oder Kugeloberfläche liegen. Die Heawood-Vermutung stellt die analoge Frage für allgemeine Oberflächen, etwa die Kleinsche Flasche (6 Farben), das Möbiusband (6 Farben), die Projektive Ebene (6 Farben) und den Torus (7 Farben). Interessanterweise ist die Verallgemeinerung – abgesehen vom Spezialfall für Ebenen oder Kugeloberflächen – wesentlich leichter zu beweisen als der Vier-Farben-Satz und kommt ohne Computerhilfe aus. J. W. Ted Youngs und Gerhard Ringel konnten im Jahre 1968 erstmal die Heawood-Vermutung für alle anderen Fälle beweisen (Satz von Ringel-Youngs). Der Vier-Farben-Satz wird also nicht durch diesen Beweis verifiziert, sondern muss gesondert behandelt werden.

Nach dem Zusammenfügen in der rechten Grafik sind jeweils die beiden gleichfarbigen „Riegel“ verbunden und bilden jeweils einen (L- bzw. X-förmigen) Körper. Da jeder Körper jeden anderen berührt, braucht man zum Färben so viele Farben wie Riegel (hier 8).

Erweitert man die Aufgabenstellung des Vier-Farben-Satzes von Oberflächen auf den euklidischen Raum selbst, dann gibt es keine Obergrenze für die Anzahl der Farben. Anstelle der „Länder“ treten dreidimensionale Gebiete ("Körper") auf, die unterschiedliche Farben haben sollen, wenn sie eine gemeinsame Grenzfläche besitzen. Für jede Zahl n lässt sich ein Beispiel konstruieren, das mindestens n Farben benötigt. Man denke sich n „lange“ kongruente Quader („Riegel“) nebeneinanderliegend, die zusammen einen Quader quadratischer Grundfläche bilden. Darauf liegen noch einmal n zu den ersten kongruente Quader nebeneinander, aber senkrecht zu den unteren, so dass alle unteren Quader alle oberen Quader berühren. Nun sei jeder der unteren mit genau einem der oberen verbunden, so dass beide gemeinsam kreuzweise einen Körper bilden. Jeder dieser Körper berührt jeden anderen; man braucht also n Farben und n war beliebig.^[1]

Bemerkung

• Die Kuratowski-Minoren
• 

  Der K₅

• 

  und der K_3,3

Wenn (so wie in der Realität häufig der Fall) ein Land auf mehrere nicht-angrenzende Gebiete verteilt ist (Kolonien, Exklaven,…), dann ist der zugehörige Graph nicht notwendigerweise planar und es sind möglicherweise mehr als vier Farben zur Färbung notwendig. Auf Planarität kann man gegebene Graphen sehr schnell testen. Nach dem Satz von Kuratowski gibt es nur genau zwei äußerst übersichtliche Graphen, die diese Eigenschaft zerstören können. Durch eine Wahl geschickter Datenstrukturen kann erreicht werden, diese „Untergraphen“, die sogenannten Kuratowski-Minoren K₅ und K_3,3, zu finden oder festzustellen, dass es sie nicht gibt, indem man jede Kante und jeden Knoten nur konstant oft betrachtet.

Die kleinste mögliche Färbung in allgemeinen Graphen G zu finden, mit anderen Worten die sogenannte Chromatische Zahl χ(G) zu bestimmen, ist sehr aufwändig (genauer: eine NP-vollständige Aufgabe). Nach den Aussagen von Tutte wäre sie gelöst, wenn man im Dualgraphen G ^* eine kleinste Gruppe gefunden hat, sodass eine gruppenwertige Strömung (das ist ein „Fluss ohne Anfang und Ende“), die nirgends das Nullelement annimmt, existiert. Diese Gruppenordnung heißt Flusszahl φ(G ^* ) und es ist für beliebige Graphen φ(G ^* ) = χ(G). Die Lösbarkeit dieses nach wie vor NP-vollständigen Problems ist unabhängig von der Struktur der vorgegebenen Gruppe und hängt nur von der Gruppenordnung ab.^[2]

Es gibt weitere Zusammenhänge des Vier-Farben-Problems mit Problemen der Diskreten Mathematik, sodass man auch Methoden der Algebraischen Topologie anwenden kann.

Fußnoten

1. ↑ C.J. Scriba, P. Schreiber: 5000 Jahre Geometrie. 2. Auflage. Springer. 2005, ISBN 3-540-22471-8, S. 454 und Abb. 7.8.3
2. ↑ Weitere Aussagen und Sätze dazu in Reinhard Diestel: Graph Theory (2000) Springer ISBN 0-387-98976-5 S. 157 ff

Literatur

• Neil Robertson, Daniel P. Sanders, Paul Seymour, Robin Thomas: A new proof of the four-colour theorem. In: Electronic Research Announcements of the American Mathematical Society. 2/1996. S. 17–25
• Kenneth Appel, Wolfgang Haken: Every Planar Map is Four Colorable. In: Contemp. Math. vol. 98, Amer. Math. Soc., Providence, RI, 1989
• Georges Gonthier: A computer-checked proof of the Four Colour Theorem. unveröffentlicht, dazu Gonthier: Formal proof- the four color theorem, Notices AMS 2008, pdf Datei
• Rudolf Fritsch, Gerda Fritsch: Der Vierfarbensatz: Geschichte, topologische Grundlagen und Beweisidee. BI-Wissenschaftverlag, 2004, ISBN 3-411-15141-2
• Robin Thomas An update on the four color theorem, Notices AMS 1998, Heft 7, pdf Datei
• Robin Wilson Four colours suffice, Princeton University Press 2002, Review in den Notices AMS, 2004, pdf Datei

Weblinks

 Commons: Vier-Farben-Satz – Sammlung von Bildern, Videos und Audiodateien

• Zusammenfassung des Beweises von Robertson, Sanders, Seymour, Thomas auf der Homepage von Robin Thomas (englisch)
• Simon Tatham's Portable Puzzle Collection Das Spiel 'Map' behandelt das Thema