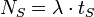Satz von Little

Littles Gesetz, auch als Littles Theorem, Satz von Little oder Formel von Little bezeichnet, ist eine bedeutende Gesetzmäßigkeit in der Warteschlangentheorie. Es wurde 1961 von John D. C. Little formuliert und bewiesen.

Littles Gesetz besagt, dass die durchschnittliche Anzahl von Kunden in einem Wartesystem, welches sich in einem stabilen Zustand befindet, gleich dem Produkt ihrer durchschnittlichen Ankunftsrate λ und ihrer durchschnittlichen Verweildauer im System t_S ist.

$N_S = \lambda \cdot t_S$

Obwohl dies intuitiv sinnvoll erscheint, ist es ein beachtenswertes Ergebnis: Es impliziert, dass dieses Verhalten vollkommen unabhängig von den benutzten Wahrscheinlichkeitsverteilungen ist und somit keine Annahmen über die Verteilung der Ankunftszeiten oder die Warteschlangendisziplin getroffen werden müssen. So ist die durchschnittliche Wartezeit bei FIFO genauso groß wie bei LIFO.

Littles Gesetz gilt nicht nur für eine isolierte Bedienstation, sondern auch für Netzwerke aus Wartesystemen. Beispielsweise kann man in einer Bank die Warteschlange eines einzelnen Schalters als Subsystem ansehen und jeden zusätzlichen Schalter als weiteres Subsystem. Littles Gesetz kann sowohl auf die Subsysteme einzeln, als auch auf das gesamte System angewendet werden. Die einzige Bedingung ist, dass das System stabil ist - es darf sich nicht in einem Übergangsstadium (Start-, Endphase) befinden.

Beispiel

Ein Maschinenarbeitsplatz soll eingerichtet werden, an welchem nur eine Bearbeitung (Job) zur gleichen Zeit ausgeführt werden kann. Zum Arbeitsplatz gehört ein Wartebereich für neu ankommende Jobs. Die mittlere Durchlaufzeit t_S = t_Warten + t_Bearbeiten sei bekannt, ebenso die Ankunftsrate neuer Jobs λ. Mit Littles Gesetz kann die mittlere Anzahl an Jobs im System N_S bestimmt werden

$N_S = \lambda \cdot t_S$

und mit dieser Information die Größe des Wartebereichs entsprechend festgelegt werden.

Literatur

• Little, J. D. C. "A Proof of the Queueing Formula L = λ W" Operations Research, 9, 383-387 (1961) (http://www.jstor.org/pss/167570).
• Arnold, Dieter; Furmans, Kai: Materialflusslehre in Logistiksystemen. 5.,erweiterte Auflage. Berlin, Heidelberg: Springer-Verlag