- Fundamentalgruppe
-
Die Fundamentalgruppe ist ein zentrales Konzept der algebraischen Topologie: Jedem geometrischen Objekt (genauer topologischen Raum) wird seine Fundamentalgruppe als ein algebraisches Objekt zugeordnet. Sie beschreibt bestimmte topologische Eigenschaften des topologischen Raumes, genauer solche, die sich bei stetigen Verformungen nicht ändern.
Durch Untersuchung der Fundamentalgruppe lässt sich oft feststellen, ob zwei Räume topologisch verschieden sind, sich also nicht ineinander verformen lassen.
Inhaltsverzeichnis
Anschauliche Erklärung am Beispiel des Torusrandes
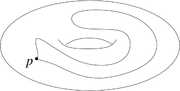
Zunächst soll an einem Beispiel die Idee der Fundamentalgruppe erklärt werden: Als topologischen Raum betrachten wir den Rand des zweidimensionalen Torus, und markieren einen Basispunkt darauf.
Von diesem Punkt aus gibt es Schleifen, d. h. geschlossene Kurven, die im Basispunkt starten, auf der Torusoberfläche verlaufen und wieder im Basispunkt enden. Manche der Schleifen lassen sich auf dem Torusrand zu einem Punkt zusammenziehen, andere nicht. Dazu stelle man sich vor, dass die Schleifen aus Gummi sind und beliebig gedehnt, gestaucht und verschoben werden dürfen, allerdings immer so, dass Anfang und Ende im Basispunkt festbleiben und die Schleifen immer auf dem Torusrand bleiben müssen (also nur auf der Oberfläche und nicht durch den „Teig“ des Donuts verlaufen). Eine solche Verformung nennt man Homotopie; man sagt auch, eine Schleife wird homotopiert. Zwei Schleifen, die sich durch eine Homotopie ineinander überführen lassen, nennt man homotop.
Alle Schleifen, die homotop zueinander sind, fasst man zu einer Homotopieklasse zusammen. Die verschiedenen Homotopieklassen bilden die Elemente der Fundamentalgruppe.
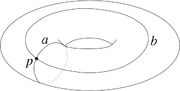
Die beiden Schleifen a und b in der Abbildung rechts gehören zum Beispiel zu verschiedenen Homotopieklassen: Sie lassen sich nicht ineinander verformen und beschreiben daher unterschiedliche Elemente der Fundamentalgruppe. Weitere Elemente bekommt man, indem man eine der beiden Schleifen mehrfach durchläuft bevor man die Schleife schließt: Eine Schleife, die zweimal um das Loch herumläuft, lässt sich nicht in eine verformen, die dreimal darum herumführt, usw.
Ganz allgemein lassen sich zwei Schleifen zu einer dritten kombinieren, indem man erst die eine, dann die andere durchläuft, also das Ende der ersten mit dem Anfang der zweiten verknüpft (da die Verknüpfungsstelle jetzt ein innerer Punkt der Schleife ist, muss sie nicht mehr unbedingt auf dem Basispunkt liegen bleiben, sondern darf von ihm auch weggeschoben werden). Mit dieser Verknüpfung wird aus der Menge der Homotopieklassen eine Gruppe, die sogenannte Fundamentalgruppe. Das neutrale Element ist die Klasse der Schleifen, die sich auf den Basispunkt zusammenziehen lassen. Das inverse Element zu einer Klasse von Schleifen erhält man, indem man diese rückwärts durchläuft.
Mathematische Definitionen
Sei X ein topologischer Raum und p ein Basispunkt in X. Eine Kurve ist eine stetige Abbildung
![\gamma: [0,1]\to X](9/6a93ee738c9209cbd6e030f37a084689.png) , und eine Schleife ist eine Kurve mit Anfangs- und Endpunkt γ(0) = γ(1) = p.
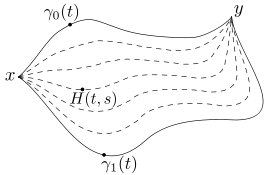
, und eine Schleife ist eine Kurve mit Anfangs- und Endpunkt γ(0) = γ(1) = p.Eine Homotopie zwischen zwei Kurven γ0 und γ1 von x nach y ist eine stetige Familie von Kurven, die beide Kurven verbindet. Mathematisch formuliert ist dies eine stetige Abbildung
![H: [0,1]\times[0,1] \to X](c/d8cf8b3206e52f6a09fb99cd0f74adde.png) mit den Eigenschaften
mit den Eigenschaften
- H(t,0) = γ0(t), H(t,1) = γ1(t) für alle t und
- H(0,s) = x, H(1,s) = y für alle s (Anfangs- und Endpunkt wird fixiert).
Der erste Parameter entspricht also dem ursprünglichen Kurvenparameter, der zweite Parameter beschreibt den Grad der Verformung der einen Kurve in die andere.
Entsprechend sind zwei Schleifen homotop, wenn es eine Homotopie zwischen ihnen gibt (mit x = y = p). Homotope Schleifen sollen als äquivalent betrachtet werden, die Äquivalenzklassen heißen Homotopieklassen. Ein beliebiges Element aus einer Homotopieklasse repräsentiert diese. Wie oben beschrieben definiert man die Fundamentalgruppe als Menge der Homotopieklassen. Man bezeichnet sie mit dem Symbol π1(X) (sprich „pi Eins von X“).
Die Gruppenstruktur erhält man durch die oben angegebene Verknüpfung, also durch Aneinanderhängen von Schleifen, wobei diese genaugenommen für Repräsentanten definiert ist. Da man jedoch aus Homotopien zwischen verschiedenen Repräsentanten auch eine Homotopie zwischen den verknüpften Schleifen konstruieren kann, ist die resultierende Homotopieklasse unabhängig von der Wahl der jeweiligen Repräsentanten.
Beispiele
- Auf einer Sphäre ab Dimension 2 lässt sich jede Schleife auf einen Punkt zusammenziehen. Daher ist die Fundamentalgruppe der Sphäre trivial, π1(Sn) = {1} (für
 ).
). - Der oben beschriebene Torusrand besitzt die Fundamentalgruppe
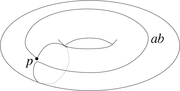
 : Die beiden Schleifen a und b sind Erzeuger der Fundamentalgruppe. Sie ist in diesem Fall abelsch: Die Schleife aba − 1b − 1 lässt sich auf einen Punkt zusammenziehen (schneidet man den Torusrand entlang von a und b auf, so erhält man ein Viereck, dessen Randkurve genau aba − 1b − 1 ist und sich im Innern des Vierecks zusammenziehen lässt). Deshalb gilt aba − 1b − 1 = 1, also ab = ba.
: Die beiden Schleifen a und b sind Erzeuger der Fundamentalgruppe. Sie ist in diesem Fall abelsch: Die Schleife aba − 1b − 1 lässt sich auf einen Punkt zusammenziehen (schneidet man den Torusrand entlang von a und b auf, so erhält man ein Viereck, dessen Randkurve genau aba − 1b − 1 ist und sich im Innern des Vierecks zusammenziehen lässt). Deshalb gilt aba − 1b − 1 = 1, also ab = ba. - Für einen n-dimensionalen Torusrand gilt
 .
. - Die zweidimensionale Ebene mit einem Loch
 hat die Fundamentalgruppe
hat die Fundamentalgruppe  , genauso wie die 1-Sphäre (ein einfacher Kreis). Die Homotopieklasse einer Schleife ist dadurch festgelegt, wie oft die Schleife um das Loch herumläuft (z.B. im Uhrzeigersinn).
, genauso wie die 1-Sphäre (ein einfacher Kreis). Die Homotopieklasse einer Schleife ist dadurch festgelegt, wie oft die Schleife um das Loch herumläuft (z.B. im Uhrzeigersinn). - Die zweidimensionale Ebene mit zwei Löchern hat als Fundamentalgruppe eine freie Gruppe in zwei Erzeugern, nämlich den beiden Schleifen, die einmal um eines der Löcher herumlaufen. Diese Gruppe ist nicht abelsch.
- Fundamentalgruppen müssen nicht torsionsfrei sein: so sind die Fundamentalgruppen der reellen projektiven Ebene oder der Gruppe der Drehungen im Raum,
 , isomorph zu
, isomorph zu  , der zyklischen Gruppe der Ordnung 2.
, der zyklischen Gruppe der Ordnung 2. - Man kann zeigen, dass es zu jeder Gruppe G einen so genannten klassifizierenden Raum BG gibt, dessen Fundamentalgruppe isomorph zu G ist.
Eigenschaften und Anwendungen
Unabhängigkeit vom Basispunkt
Da alle Schleifen am Basispunkt beginnen, misst die Fundamentalgruppe nur Eigenschaften der Zusammenhangskomponente, in der p liegt. Daher ist es sinnvoll anzunehmen, dass X wegzusammenhängend ist. Dann ist jedoch auch die Wahl des Basispunktes für die Fundamentalgruppe nicht wesentlich: Nimmt man einen anderen Basispunkt q, so lassen sich Schleifen von p nach q verschieben, indem man von q aus erst eine fest gewählte Kurve nach p geht, dann die ursprüngliche Schleife und dann die gleiche Kurve zurück nach q. Bei der Verknüpfung von zwei Schleifen in q heben sich die Zwischenwege genau auf. Die Fundamentalgruppen bzgl. p und q sind daher isomorph; der Isomorphismus hängt im Allgemeinen jedoch vom gewählten Weg von q nach p ab.
Ist X nicht wegzusammenhängend, so kann die Fundamentalgruppe durchaus vom gewählten Basispunkt
 abhängen. Man schreibt dann genauer π1(X,p). Nach obigem Argument erhält man für jeden anderen Basispunkt aus derselben Wegzusammenhangskomponente, in der p liegt, eine isomorphe Gruppe.
abhängen. Man schreibt dann genauer π1(X,p). Nach obigem Argument erhält man für jeden anderen Basispunkt aus derselben Wegzusammenhangskomponente, in der p liegt, eine isomorphe Gruppe.Überlagerungen
Die Fundamentalgruppe spielt eine entscheidende Rolle bei der Klassifikation von Überlagerungen. Für Räume, die eine universelle Überlagerung besitzen, ist die Fundamentalgruppe isomorph zur Decktransformationsgruppe der universellen Überlagerung. Dieser Isomorphismus ist eines der wichtigsten Hilfsmittel zur Berechnung der Fundamentalgruppe.
Satz von Seifert-van-Kampen
Ein wichtiges Hilfsmittel zur Berechnung der Fundamentalgruppe ist auch der Satz von Seifert-van-Kampen, der es erlaubt, den Raum X in sich überlappende Bereiche zu zerlegen und die Fundamentalgruppe von X aus den (einfacheren) Fundamentalgruppen der Bereiche und der Überlappung auszurechnen.
Folgerungen aus bestimmten Fundamentalgruppen
Die Kenntnis der Fundamentalgruppe erlaubt oft Rückschlüsse auf den topologischen Raum. Hat zum Beispiel eine Mannigfaltigkeit eine endliche Fundamentalgruppe, so kann sie keine Metrik tragen, die überall nichtpositive Krümmung hat. Die einzige geschlossene Fläche mit trivialer Fundamentalgruppe ist die Sphäre. Die mittlerweile bewiesene Poincaré-Vermutung besagt, dass eine analoge Aussage auch für dreidimensionale Mannigfaltigkeiten gilt.
Zusammenhang mit Homologie
Im allgemeinen Fall braucht die Fundamentalgruppe nicht (wie beim Torusrand) abelsch zu sein. Man kann sie aber abelsch „machen“, indem man die Kommutatorgruppe herausteilt. Die Gruppe, die man dann erhält, ist isomorph zur ersten Homologiegruppe.
Verallgemeinerungen
Die Fundamentalgruppe ist die erste Homotopiegruppe, daher kommt auch die Bezeichnung π1. Da die Definition eindimensionale Schleifen benutzt, kann die Fundamentalgruppe nur die eindimensionale topologische Struktur erkennen. Ein Loch in einer zweidimensionalen Fläche lässt sich durch Schleifen feststellen, ein Loch im dreidimensionalen Raum (etwa
 ) jedoch nicht: sie lassen sich daran vorbeiziehen.
) jedoch nicht: sie lassen sich daran vorbeiziehen.Die Verallgemeinerung zur n-ten Homotopiegruppen πn benutzt daher statt Schleifen Sphären der Dimension n.
Falls π1 = {1}, so besagt der Satz von Hurewicz (nach Witold Hurewicz), dass die erste nichttriviale Homotopiegruppe mit der ersten nichttrivialen Homologiegruppe übereinstimmt.
Die nullte Homotopiegruppe π0 ist im Allgemeinen keine Gruppe, sondern nur eine Menge, nämlich die Menge der Wegzusammenhangskomponenten von X. Für manche Räume gibt es aber trotzdem eine kanonische Gruppenstruktur, etwa für die Schleifenräume, da π0(Ω(X,x)) = π1(X,x) gilt.
Literatur
- Tammo tom Dieck: Topologie, de Gruyter, Berlin, 2000, ISBN 3-11-016236-9
- Allen Hatcher: Algebraic topology, CUP, Cambridge, 2003, ISBN 0-521-79160-X (auch Algebraic Topology)
Wikimedia Foundation.