Satz von Steiner-Lehmus

$|AE|=|BD|,\,\alpha=\beta,\, \gamma=\delta$ $\Rightarrow \triangle ABC \text{ ist gleichschenklig}$

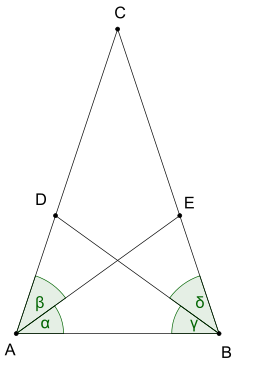
Der Satz von Steiner-Lehmus ist ein Satz der Elementargeometrie über Dreiecke. Er wurde zuerst von C. L. Lehmus formuliert und dann von Jakob Steiner bewiesen.

Sind in einem Dreieck 2 Winkelhalbierende gleichlang, so ist es gleichschenklig.

Der Satz wurde zum ersten Mal 1840 in einen Brief von C. L. Lehmus an C. Sturm erwähnt, in welchem dieser C. Sturm um einen elementargeometrischen Beweis der Aussage bat. C. Sturm verbreitete das Problem unter anderen Mathematikern und Jakob Steiner war einer der Ersten, der einen Beweis erbrachte. Seitdem wurde der Satz zu einem beliebten Gegenstand der Elementargeometrie, zu dem in den folgenden 160 Jahren zahlreiche Publikationen erschienen. ^[1][2]

Einzelnachweise

1. ↑ Coxeter, H. S. M. and Greitzer, S. L. "The Steiner-Lehmus Theorem." §1.5 in Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 14-16, 1967.
2. ↑ Diane and Roy Dowling: The Lasting Legacy of Ludolph Lehmus. Manitoba Math Links -Volume II- Issue 3, Spring 2002 (engl.)

Weblinks

• Florian Modler: Vergessene Sätze am Dreieck (Teil 2), Matroids Matheplanet, 27. August 2006
• Eric W. Weisstein: Steiner-Lehmus theorem (engl.). In: MathWorld. (englisch)
• Paul Yiu: Euclidean Geometry Notes, Skript, Florida Atlantic University, S. 15-16 (englisch)
• Torsten Sillke: Steiner-Lehmus Theorem, Sammlung verschiedener Beweise zum Satz von Steiner-Lehmus (engl.)