Signum (Mathematik)

Der Begriff Signum (lateinisch für Zeichen) wird in der Mathematik in zwei Zusammenhängen verwendet, beide Male im Sinne eines „Vorzeichens“.

Signumfunktion auf den reellen Zahlen

Graph der Vorzeichenfunktion

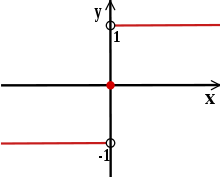
Die Signumfunktion (auch Vorzeichenfunktion) ist eine Funktion aus der Menge der reellen Zahlen in die Menge {−1, 0, 1} und wird in der Regel wie folgt definiert:

$\sgn(x):= \begin{cases} +1 & \; x>0 \\ \;\;\,0 & \; x=0 \\ -1 & \; x<0 \\ \end{cases}$

Sie ordnet jedem x > 0 eine +1, x = 0 eine 0 und jedem x < 0 eine −1 zu.

Bei Anwendungen in der Rechentechnik verzichtet man meist auf eine Sonderstellung der 0, indem man sie den positiven, negativen oder beiden Zahlenbereichen zuordnet. Dadurch lässt sich das Vorzeichen einer Zahl in einem einzigen Bit kodieren. Die Signumfunktion ist darüber hinaus die schwache Ableitung der Betragsfunktion.

Signumfunktion auf den komplexen Zahlen

Signum von vier komplexen Zahlen

Im Vergleich zum Signum reeller Zahlen wird nur selten die folgende Erweiterung auf komplexe Zahlen betrachtet:

$\sgn(z)= \begin{cases} \frac {z} {|z|} & \; z\ne 0 \\ 0 & \; z=0 \\ \end{cases}$

Das Ergebnis dieser Funktion liegt auf dem Einheitskreis und besitzt dasselbe Argument wie der Ausgangswert, insbesondere gilt

$\sgn\left(r\mathrm e^{\mathrm i\varphi}\right)=\mathrm e^{\mathrm i\varphi},\qquad\mathrm{falls}\ r>0.$

Beispiel (im Bild rot):

$\operatorname{sgn}(z_1) = \operatorname{sgn}(2 + 2\mathrm i) = \frac {2 + 2\mathrm i} {\left| 2 + 2\mathrm i \right|} = \frac {2 + 2\mathrm i} {2\sqrt2} = \frac {1 + \mathrm i} {\sqrt{2}} = \frac12\sqrt2+\frac{\mathrm i}2\sqrt2.$

Rechenregeln

Es gelten die folgenden Rechenregeln in Bezug auf die Signumfunktion angewendet auf die komplexen Zahlen z und w:

• $z=|z|\cdot\sgn z$ für alle z, wobei $|\cdot |$ für die Betragsfunktion steht
• $\sgn(z\cdot w)=\sgn z\cdot\sgn w$, insbesondere
  • $\sgn(\lambda\cdot z)=\sgn z$ für positive reelle λ
  • $\sgn(\lambda\cdot z)=-\sgn z$ für negative reelle λ
  • $\operatorname{sgn}(-z) = -\operatorname{sgn}(z)$
• $\operatorname{sgn}(|z|) = |\operatorname{sgn}(z)|$
• $\operatorname{sgn}(\bar z) = \overline{\operatorname{sgn}(z)}$ mit der komplexen Konjugation
• Falls $z\ne0$ ist, gilt auch

$\operatorname{sgn}\left(\frac{1} {z}\right) = \frac {1} {\operatorname{sgn}(z)} = \overline{\operatorname{sgn}(z)}$

Signum von Permutationen

Jede Permutation einer endlichen Menge lässt sich entweder aus einer geraden oder aus einer ungeraden Zahl von Transpositionen, also Vertauschungen von nur zwei Elementen, zusammensetzen. Im ersten Fall hat die Permutation das Signum 1, im zweiten Fall das Signum -1. Dies ist äquivalent dazu, dass die Anzahl der Fehlstände der Permutation gerade bzw. ungerade ist, also eine fixe Parität hat.

Eine rein formale Definition des Signums einer Permutation der Menge $\left\{1,2,\ldots ,n\right\}$ ist durch folgende Abbildung gegeben:

$\begin{align} \operatorname{sign}: S_n & \to\mathbb Z^\times=\{-1,1\}\\ \sigma&\mapsto\prod_{1\le i<j\le n} \frac{\sigma(i)-\sigma(j)}{i-j} \end{align}$

Dabei ist S_n die Menge aller Permutationen einer n-elementigen Menge (die symmetrische Gruppe) und σ ein Element von S_n. Ferner bezeichnet σ(i) dasjenige Element einer n-elementigen Menge M, auf welches das i-te Element dieser Menge M vermöge σ abgebildet wird.

Das Signum $\operatorname{sign}\sigma$ einer Permutation σ ist 1, falls σ eine gerade Anzahl von Fehlständen hat, und −1, falls σ eine ungerade Anzahl von Fehlständen hat. Unter einem Fehlstand der Permutation σ versteht man hierbei ein Paar $\left(i,j\right)$ von Elementen i und j der Menge $\left\{1,2,\ldots,n\right\}$ mit i < j und $\sigma\left(i\right)>\sigma\left(j\right)$.

Ableitung der Signumfunktion

Die Signumfunktion ist weder klassisch differenzierbar, noch besitzt sie eine schwache Ableitung. Allerdings ist sie im Sinne von Distributionen differenzierbar, und ihre Ableitung ist 2δ, wobei δ die Delta-Distribution bezeichnet.

Siehe auch

• Sprungfunktion

Literatur

• Königsberger: Analysis 1. 6 Auflage. Springer, Berlin 2003, ISBN 354040371X, S. 101 (Signum auf den reellen Zahlen).
• Hildebrandt: Analysis 1. 2 Auflage. Springer, Berlin 2005, ISBN 3540253688, S. 133 (Signum auf den reellen Zahlen).