- Formelsammlung Algebra
-
Die Formelsammlung zur Algebra ist ein Teil der Formelsammlung, in der auch Formeln der anderen Fachbereiche zu finden sind.
Grundrechenarten
Siehe dazu: Formelsammlung Grundrechenarten.
Arithmetische Notation
Es gilt: Punkt- vor Strichrechnung. Das heißt Mal und Geteilt binden stärker als Plus und Minus.
Bei Verwendung der Polnischen Notation bzw. der Umgekehrten Polnischen Notation bedarf es keiner Klammerung.
Axiome
- Kommutativ-Gesetz (Vertauschungsgesetz)
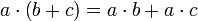 (linksdistributiv)
(linksdistributiv)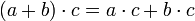 (rechtsdistributiv)
(rechtsdistributiv)
Elementare Funktionen
Potenzen
- Definition Potenzen
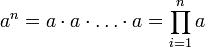 (n Faktoren)
(n Faktoren)
- formal (induktiv):
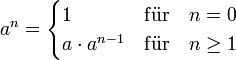
- Begriffe zu Potenzen
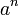 (das Ergebnis der Rechnung) ist die Potenz
(das Ergebnis der Rechnung) ist die Potenz
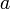 ist die Basis
ist die Basis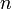 ist der Exponent
ist der Exponent
- Potenzen mit gleicher Basis
- Potenzieren einer Potenz
- Potenzen mit gleichem Exponenten
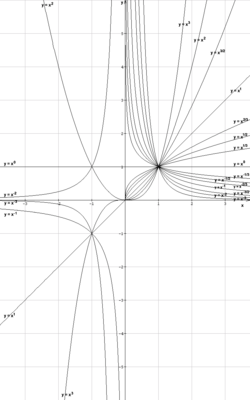
Potenzfunktionen mit ganzzahligem Exponenten
- 1. n positiv und gerade (
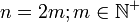 )
)
-
-
- Gemeinsame Punkte aller Funktionsgraphen
-
- 2. n positiv und ungerade (
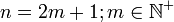 )
)
-
-
- Gemeinsame Punkte aller Funktionsgraphen
-
- 3. n negativ und gerade (
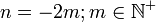 )
)
-
-
- Diese Funktionen besitzen keine Nullstellen!
-
-
-
- Gemeinsame Punkte aller Funktionsgraphen
-
- 4. n negativ und ungerade (
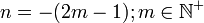 )
)
-
-
- Diese Funktionen besitzen keine Nullstellen!
-
-
-
- Gemeinsame Punkte aller Funktionsgraphen
-
Potenzfunktionen mit gebrochenen Exponenten (Wurzelfunktionen)
-
-
- Gemeinsame Punkte aller Funktionsgraphen
-
Wurzeln
- Begriffe zu Wurzeln
![x = \sqrt[n]{a}](/pictures/dewiki/52/469c5e753bca6920bc3a41f0f2cbf136.png)
- n ist der Wurzelexponent
- a ist der Radikand
- Definition Wurzel
- Negativer Radikand und ungerader Exponent
Für
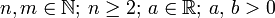 gelten folgende Regeln
gelten folgende Regelnund die Regeln können auf
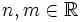 erweitert werden.
erweitert werden.Logarithmus
- Definition des Logarithmus zur Basis b
- Logarithmus-Gesetze
- Basiswechsel
Logarithmusfunktionen
-
- Gemeinsame Punkte aller Funktionsgraphen
-
- Spezialfälle
Exponentialfunktionen
-
- Diese Funktionen besitzen keine Nullstellen!
-
- Gemeinsame Punkte aller Funktionsgraphen
-
- Spezialfall
Gesetze der Anordnung
Betrag, Signum, Gaußklammer
Betrag:
Signum:
Das Signum einer komplexen Zahl ≠ 0 ist gleich die Zahl geteilt durch ihren Betrag, also sign(z)=z/|z|.
Also gilt:
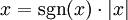
Die Gaußklammer einer (reellen) Zahl ist die größte ganze Zahl, die kleiner als die Zahl selbst ist.
Termumformungen
8 - (2 − a + b)
Hier ist die „Minusklammer“ zu beachten. Minusklammer heißt, dass vor der Klammer ein Minus (-) steht. Somit müssen alle Werte in der Klammer mit (−1) multipliziert werden.
= 8 + (2·(−1) − a·(−1) + b·(−1)) = 8 - 2 + a − b = 6 + a − b
Generell dürfen bei einer Gleichung folgende Termumformungen durchgeführt werden
- Addition (und folglich auch Subtraktion) derselben Zahl oder Variablen auf beiden Seiten des Gleichheitszeichens
- Multiplikation (und folglich auch Division) derselben Zahl ungleich Null auf beiden Seiten des Gleichheitszeichens
sowie
- Klammern auflösen
- Seiten vertauschen
- Summanden vertauschen
jeweils auf einer Seite der Gleichung.
Beispiel:
3(2x-1) + 2 = x | Klammer auflösen (Distributivgesetz)
- 6x - 3 + 2 = x | Zusammenfassen
- 6x - 1 = x | - 6x
- - 1 = -5x | :(-5)
- 1/5 = x
Grundlegende Funktionen
Definition
In der Mathematik ist eine Funktion oder Abbildung eine Beziehung zwischen zwei Mengen, die jedem Element der einen Menge (Eingangsgröße, Funktionsargument, unabhängige Variable, x-Wert) ein Element der anderen Menge (Ausgangsgröße, Funktionswert, abhängige Variable, y-Wert) zuordnet:
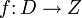 oder
oder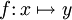
Gerade Funktion
- Der Graph liegt somit symmetrisch zur y-Achse!
Ungerade Funktion
- Der Graph liegt somit zentralsymmetrisch zum Koordinatenursprung!
Lineare Funktionen
 und
und 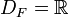
-
- Schnittpunkte mit der y-Achse
-
 Schnittwinkel des Graphen mit der x-Achse
Schnittwinkel des Graphen mit der x-Achse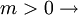 steigende Gerade
steigende Gerade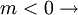 fallende Gerade
fallende Gerade
Lineare Gleichungssysteme
Ein System aus
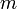 linearen Gleichungen mit
linearen Gleichungen mit 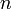 Variablen
Variablen 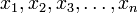 wird lineares Gleichungssystem genannt.
wird lineares Gleichungssystem genannt.Jedes derartige Gleichungssystem lässt sich in folgender Form darstellen:
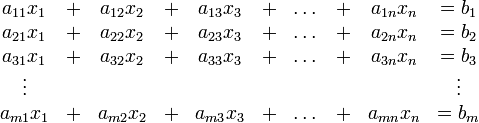
Homogene und Inhomogene Systeme
Ein Lineares Gleichungssystem, bei dem alle Konstanten
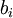 (Absolutglieder) den Wert
(Absolutglieder) den Wert 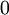 haben, heißt homogen.
haben, heißt homogen.Sind nicht alle Absolutglieder gleich
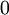 , so wird das System inhomogen genannt.
, so wird das System inhomogen genannt.Gleichsetzungsverfahren
Bei dem Gleichsetzungsverfahren zum Lösen von Linearen Gleichungssysteme werden die einzelnen Gleichungen zunächst zu einer gemeinsamen Variable umgeformt und dann gleichgesetzt:
Diese beiden Gleichungen werden nun nach
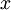 umgestellt:
umgestellt:Nun kann man diese beiden Gleichungen gleichsetzen, da sie von ihren Werten her identisch sind (
 ):
):Hierbei erhält man zwei Lösungen, was darauf hinweist, dass das System zwei Lösungen hat. Diese Lösungen setzt man in eine der beiden Ausgangsgleichungen (bzw. deren umgestellte Variante) ein und erhält jeweils die Variable x dazu:
Somit hat das Gleichungssystem zwei Lösungen:
Additionsverfahren
Wie der Name schon im Ansatz verrät, werden mit Hilfe des Additionsverfahren Gleichungen addiert. Dies geschieht in der Regel so, dass eine oder gleich mehrere Variablen in den Gleichungen eliminiert werden:
Dazu muss eine der beiden Gleichungen so umgeformt werden, dass bei einer Addition der beiden Gleichungen eine Variable verschwindet. In diesem Beispiel multiplizieren wir dazu Gleichung (2) auf beiden Seiten mit
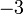 :
:Dadurch erhalten wir ein gleichwertiges Gleichungssystem, in dem der Term
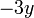 vorkommt:
vorkommt:Nun werden beide Gleichungen des Systems addiert und somit in einer Gleichung zusammengefasst:
Anschließend wird nach der verbliebenen Variablen
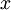 aufgelöst:
aufgelöst:Dadurch erhalten wir die Lösungsmenge:
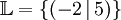 . Damit ist der Wert der ersten Variable bekannt. Diesen Wert (
. Damit ist der Wert der ersten Variable bekannt. Diesen Wert (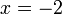 ) setzen wir in Gleichung (1) ein, um den Wert der zweiten Variable zu berechnen:
) setzen wir in Gleichung (1) ein, um den Wert der zweiten Variable zu berechnen:Einsetzungsverfahren
Die Idee hinter dem Einsetzungsverfahren ist folgende: Man löst eine der Gleichungen nach einer Variablen auf und setzt diese Variable dann in die anderen Gleichungen ein. Dadurch wird eine Variable eliminiert.
Bei einem Gleichungssystem mit zwei Gleichungen und zwei Variablen geht man so vor:
- Schritt 1: Auflösung einer Gleichung nach einer Variablen
- Schritt 2: Einsetzen dieser Variablen in die anderen Gleichung
- Schritt 3: Auflösen der im Schritt 2 erhaltenen Gleichung nach der enthaltenen Variablen
- Schritt 4: Einsetzen der Lösung in die nach Schritt 1 umgeformten Gleichung
Gegeben ist folgendes Gleichungssystem:
Schritt 1:
Eine der beiden Gleichungen muss nach x oder y aufgelöst werden. In diesem Beispiel wird die 2. Gleichung nach y aufgelöst.
Schritt 2:
Danach können wir in der ersten Gleichung das y durch den Term (17 − 9x) ersetzen und bekommen dann:
Schritt 3:
Diese Gleichung können wir nun nach x auflösen.
Schritt 4:
Die Lösung x = 2 wird in die umgestellte Gleichung (2) eingesetzt:
Die Lösungsmenge ist somit:
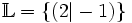 .
.Quadratische Gleichungen
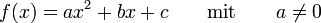 und
und 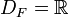
-
-
-
-
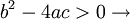 zwei verschiedene Nullstellen
zwei verschiedene Nullstellen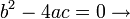 genau eine (Doppel-)Nullstelle
genau eine (Doppel-)Nullstelle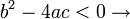 keine reelle Nullstelle
keine reelle Nullstelle
-
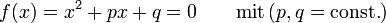
-
- Lösungen
-
-
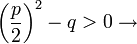 zwei verschiedene Nullstellen
zwei verschiedene Nullstellen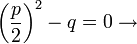 genau eine (Doppel-)Nullstelle
genau eine (Doppel-)Nullstelle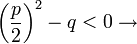 keine reelle Nullstelle
keine reelle Nullstelle
-
- Zerlegung in Linearfaktoren
-
-
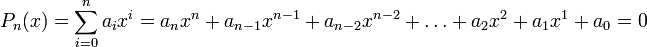
-
- Lösungen (Nullstellen)
-
-
- Zerlegung in Linearfaktoren
-
-
- Lösungsverfahren
-
- Ist
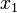 eine durch Probieren gefundene Nullstelle, so kann
eine durch Probieren gefundene Nullstelle, so kann 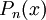 mittels Polynomdivision ohne Rest durch
mittels Polynomdivision ohne Rest durch 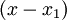 dividiert werden. Man erhält dadurch eine Gleichung (ein Polynom) (
dividiert werden. Man erhält dadurch eine Gleichung (ein Polynom) (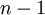 )-ten Grades und es gilt:
)-ten Grades und es gilt: 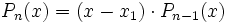 .
.
- Ist
-
- Sei n der Grad (also die höchste vorkommende Potenz der Lösungsvariablen x) der Gleichung. Werden mehrfache Nullstellen entsprechend ihrer Vielfachheit gezählt, hat die Gleichung n (komplexe) Nullstellen.
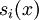 wird so gewählt, dass
wird so gewählt, dass 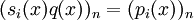 , dass also die Koeffizienten der höchsten in p vorkommenden Potenz gleich sind.
, dass also die Koeffizienten der höchsten in p vorkommenden Potenz gleich sind.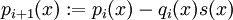
- Gilt
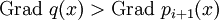 , so wird abgebrochen.
, so wird abgebrochen. - i wird inkrementiert und die Schleife erneut durchlaufen
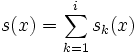
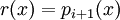
- f(x): = x2 − 2x − 8
- arithmetisches Mittel von a und b:
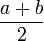
- allgemeiner Ansatz:
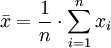
- geometrisches Mittel von a und b:
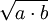
- allgemeiner Ansatz:
![\bar x = \sqrt[n]{\prod_{i=1}^n x_i}](/pictures/dewiki/55/79947223930d8a7effecc45492b0a9f8.png)
- Der Wert, welcher in einer geordneten Liste genau in der Mitte steht, bzw. bei zwei Werten in der Mitte das arithmetische Mittel dieser.
- z. B.: 1, 2, 3
 Zentralwert = 2
Zentralwert = 2 - z. B.: 1, 2, 3, 4
 Zentralwert = (2+3)/2 = 2,5
Zentralwert = (2+3)/2 = 2,5 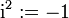
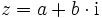 mit
mit 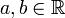
-
- Polarform
- Exponentialform
- Polarform
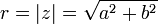 ;
;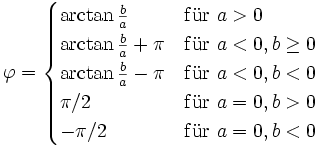
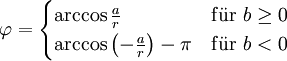
- Addition
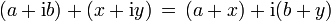
- Subtraktion
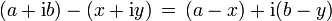
- Multiplikation
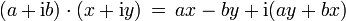
- Division
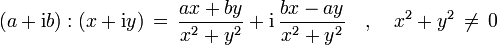
- Quadratwurzel
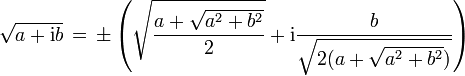
- Induktionsanfang: Man beweise P zunächst für n = N
- Induktionsschritt: Man zeige, dass P(n+1) aus P(n) folgt.
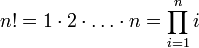
- 0! = 1
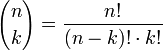
- (a + b)0 = 1
- (a + b)1 = a + b
- (a + b)2 = a2 + 2ab + b2
- (a + b)3 = a3 + 3a2b + 3ab2 + b3
- (a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
- …
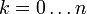
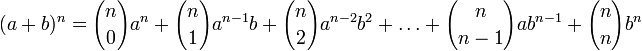
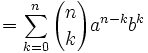
- N. b.
- : Der Relative Fehler
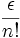 ist bei großem n klein. Das gilt nicht notwendigerweise für den absoluten Fehler. Es gilt:
ist bei großem n klein. Das gilt nicht notwendigerweise für den absoluten Fehler. Es gilt: ![n! = \left(\frac{n}{e}\right)^n \cdot \sqrt{2 \pi n} \cdot \left[1 + \mathcal{O}(1/n)\right]](/pictures/dewiki/97/a587083c96cbde40bfc004d8d7a8caf9.png)
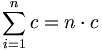 (Summation über n konstante Glieder ist soviel wie Multiplikation mit n)
(Summation über n konstante Glieder ist soviel wie Multiplikation mit n)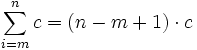 (Summation über n-m+1 konstante Glieder)
(Summation über n-m+1 konstante Glieder)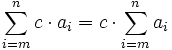 (Konstanter Faktor kann vor das Summenzeichen gezogen werden)
(Konstanter Faktor kann vor das Summenzeichen gezogen werden)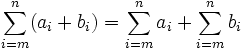 (Reihenfolge der Summanden kann beliebig geändert werden)
(Reihenfolge der Summanden kann beliebig geändert werden)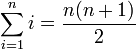 (Summe der ersten n natürlichen Zahlen, Der kleine Gauß)
(Summe der ersten n natürlichen Zahlen, Der kleine Gauß)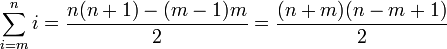 (Summe eines Bereiches von m bis n natürlichen oder ganzen Zahlen)
(Summe eines Bereiches von m bis n natürlichen oder ganzen Zahlen)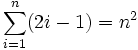 (Summe der ersten n ungeraden Zahlen)
(Summe der ersten n ungeraden Zahlen)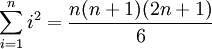 (Summe der ersten n Quadratzahlen)
(Summe der ersten n Quadratzahlen)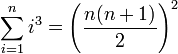 (Summe der ersten n Kubikzahlen)
(Summe der ersten n Kubikzahlen)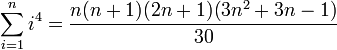 (Summe der ersten n Potenzen mit Exponenten 4)
(Summe der ersten n Potenzen mit Exponenten 4)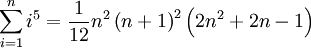 (Summe der ersten n Potenzen mit Exponenten 5)
(Summe der ersten n Potenzen mit Exponenten 5)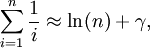 mit der Euler-Mascheroni-Konstante γ (gamma).
mit der Euler-Mascheroni-Konstante γ (gamma).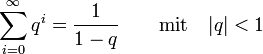 (unendliche geometrische Reihe)
(unendliche geometrische Reihe)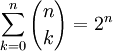 (setze a = 1,b = 1)
(setze a = 1,b = 1)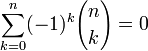 (setze a = − 1,b = 1)
(setze a = − 1,b = 1)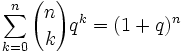 (setze a = 1,b = q)
(setze a = 1,b = q)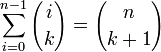
- G = Grundwert
- p = Prozentzahl
- p % = Prozentsatz
- W = Prozentwert
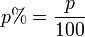
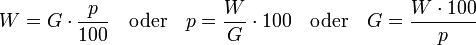
- Vermehrter Grundwert
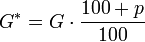
- Verminderter Grundwert
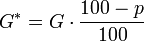
- Verzinsung
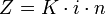
- Endkapital
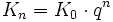
- Rentenrate für R0
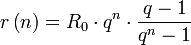
- Rentenrate für Rn
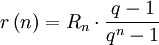
- Rentenendwert
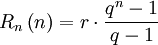
- Rentenbarwert
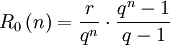
- Rentenrate für R0
- Rentenrate für Rn
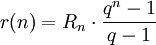
- Rentenendwert
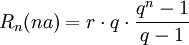
- Rentenbarwert
- Jährlicher (j) Abschreibungsbetrag (Lineare Abschreibung)
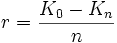
- Jährlicher Abschreibungsbetrag (Geometrisch degressive Abschreibung)
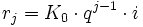
- Ansparen mit vorschüssigen Raten
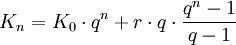
- Abzahlen mit vorschüssigen Raten
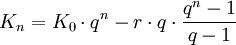
- Ansparen mit nachschüssigen Raten
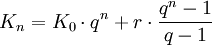
- Abzahlen mit nachschüssigen Raten
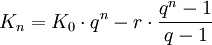
Normalform
Gleichungen n-ten Grades
Polynome n-ten Grades
Polynomdivision
Aufspaltung des Quotienten der Polynome 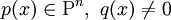 wie folgt:
wie folgt:
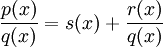
Damit 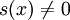 ist und damit die Polynomdivision sinnvoll ist, muss für den Grad der Polynome gelten:
ist und damit die Polynomdivision sinnvoll ist, muss für den Grad der Polynome gelten:
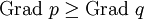 .
.
Nun wird 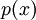 schrittweise dividiert (
schrittweise dividiert (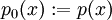 ):
):
Nach Abbruch gilt
Horner-Schema
Mit dem Hornerschema lässt sich die Berechnung von Funktionswerten für ein Polynom vereinfachen. Beispiel:
Dazu legt man eine Tabelle an. Die Anzahl der Zeilen ist drei, die der Spalten um zwei größer als der Grad des Polynoms (für das Beispiel also vier Spalten). Die Koeffizienten schreibt man, von der zweiten Spalte beginnend, in die erste Zeile. Den x-Wert schreibt man in die erste Spalte der zweiten Zeile. Beginnend mit der zweiten Spalte werden die oberen beiden Zahlen addiert. Der Faktor der zweiten Zeile der nächsten Spalte ergibt sich aus der Multiplikation der voranstehenden Summe mit dem x-Wert. Kurz: Senkrecht wird summiert, schräg wird multipliziert. Der Funktionswert befindet sich zum Schluss in der dritten Zeile der letzten Spalte.
Beispiel für f( − 2):
1 −2 −8 x=−2 −2 8 --------------- 1 −4 0
Sollte der Funktionswert, wie hier, Null sein, sind die restlichen Zahlen in der letzten Zeile das Ergebnis der Polynomdivision der Funktion durch x minus den Wert, hier x − ( − 2): f(x) = (x − 4)(x + 2)
Mittelwerte
Komplexe Zahlen
Definition
a wird als Realteil und b als Imaginärteil bezeichnet.
Komplexe Konjugation
Dreht man das Vorzeichen des Imaginärteils b einer komplexen Zahl 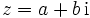 um, so erhält man die zu z konjugiert komplexe Zahl
um, so erhält man die zu z konjugiert komplexe Zahl 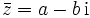 (manchmal auch z * geschrieben).
(manchmal auch z * geschrieben).
Polarform und Exponentialform
r wird als Betrag und  wird als Argument von z bezeichnet. (genauere Erklärung unter Komplexe Zahl)
wird als Argument von z bezeichnet. (genauere Erklärung unter Komplexe Zahl)
Umrechnungsformeln
für 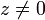 wird das Argument wie folgt bestimmt:
wird das Argument wie folgt bestimmt:
oder
Rechenregeln
Vollständige Induktion
Zu beweisen ist eine Behauptung P für alle Natürlichen Zahlen, die größergleich sind als N
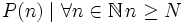
Bemerkung: Im Regelfall will man P(n) für alle Natürlichen Zahlen zeigen, damit ist N=1 und der Induktionsanfang ist für n=1 zu beweisen
Kombinatorik
Fakultät
Die Fakultät von 0 ist als 1 definiert, da ein leeres Produkt vorliegt.
Fakultäten für nichtnatürliche Zahlen (negative/gebrochene/komplexe) Zahlen sind nicht definiert, als Ersatz kann die Gammafunktion dienen.
Binomialkoeffizient („n über k“)
Binomischer Satz/Pascalsches Dreieck
Schreibt man die Koeffitienten von (a + b)n zeilenweise, d. h. die von (a + b)n in Zeile n, erhält man das Pascalsche Dreieck. n über k ist daher die k-te Zahl in der n-ten Reihe dieses Zahlendreiecks.
Stirlingsche Näherungsformel
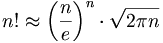
Summenformeln
Hintergrundinformation in den Artikeln Summe und Reihe. Erklärungen zum Summenzeichen ebenfalls im Artikel Summe.
Rechenregeln
Arithmetische Reihen
Potenzsummen
Allgemein kann die Summe der ersten i natürlichen Zahlen, jeweils zur k-ten Potenz erhoben, mit der Faulhaberschen Formel berechnet werden.
Harmonische Reihe
Geometrische Reihe
Reihen mit Binomialkoeffizienten
Spezialfälle dieser Formel sind:
Eine weitere Eigenschaft der Binomialkoeffizienten, die sich am pascalschen Dreieck ablesen lässt, ist die folgende:
Prozentrechnung
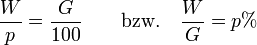
Oft benutzte Prozentsätze
| Prozentsatz | 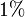 |
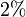 |
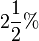 |
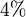 |
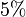 |
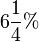 |
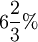 |
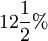 |
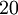 |
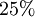 |
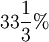 |
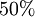 |
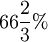 |
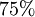 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Anteil am Grundwert | 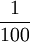 |
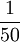 |
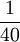 |
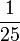 |
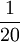 |
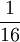 |
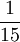 |
 |
 |
 |
 |
 |
 |
 |
Zinsrechnung
| K0 | Anfangskapital |
| Kn | Endkapital (nach n Zinsperioden) |
| n | Laufzeit |
| p | Zinsfuß (Zinssatz in Prozent) |
| i | Zinssatz (mit i = p/100) |
| q | Zinsfaktor (mit q = 1 + i) |
| r | Rentenrate |
| R0 | Rentenbarwert (zum Zeitpunkt t = 0) |
| Rn | Rentenendwert (nach n geleisteten Rentenzahlungen) |
| r | konstante Rentenrate oder Rate |
| n | Anzahl der Rentenperioden (Anzahl der Jahre, die der Rentenvorgang andauert) |
| p | Zinssatz der Verzinsung der Rentenraten bzw. des Kapitalbestandes |
Als Zinsperiode wird i. d. R. das Kalenderjahr, eingeteilt in 12 Monate mit je 30 Zinstagen gewählt.
Einfache Zinsrechnung:
Zinseszins:
Rentenrechnung
Je nachdem, zu welchem Zeitpunkt innerhalb der zugehörigen Zeitperiode die Rente zur Auszahlung kommt, unterscheidet man zwischen einer vorschüssigen Rente (pränumerando), wenn sie am Anfang, und einer nachschüssigen Rente (postnumerando), wenn sie am Ende des zugehörigen Zeitintervalls ausgezahlt wird.
Rentenrechnung (Nachschüssige Rentenzahlungen)
Rentenrechnung (Vorschüssige Rentenzahlungen)
Abschreibung
Sparkassenformel
Wikimedia Foundation.

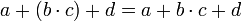
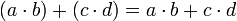
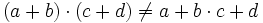
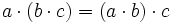
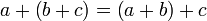
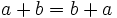
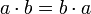
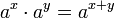
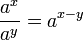
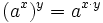
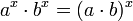
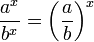
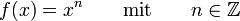
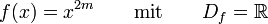
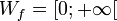
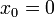
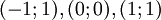
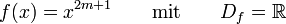
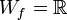
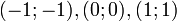
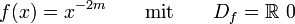
![\!\,W_f = ]0; + \infty[](/pictures/dewiki/57/95031cdc0675236637f57eb97b93a596.png)
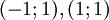
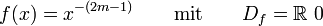
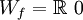
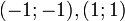
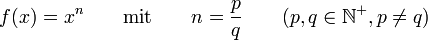
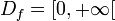
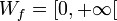
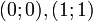
![x^n = a \Leftrightarrow x = \sqrt[n]{a} \qquad \left(a \in \mathbb{R},a \geq 0, n \in \mathbb{N^+}\right)](/pictures/dewiki/50/2e273726f37e8a0e25d753038966d85c.png)
![\sqrt[n]{-a}=-\sqrt[n]{a}\qquad \left(a \in \mathbb{R}, n \in \mathbb{N^+}, n=2u-1,u \in \mathbb{N^+}\right)](/pictures/dewiki/54/6b5f5563c5580d9f03ac0955eeeb6e21.png)
![\sqrt[n]{a} = a^\frac{1}{n}](/pictures/dewiki/50/2009af813099ac7b1bef0f0fb92a7999.png)
![\sqrt[n]{a ^m} = ({\sqrt[n]{a}}) ^m = a^\frac{m}{n}](/pictures/dewiki/49/1fc7098fb734266421f03f8a174df125.png)
![\sqrt[n]{a} \cdot \sqrt[n]{b} = \sqrt[n]{a \cdot b}](/pictures/dewiki/55/73d577cd0a118df1dda404e72e4a922d.png)
![{{ \sqrt[n]{a}} \over {\sqrt[n]{b}}} = \sqrt[n]{a \over b}](/pictures/dewiki/55/732a5198e723d90097121b71e3ca3c57.png)
![\sqrt[n]{{\sqrt[m]{a}}} = \sqrt[n \cdot m]{a}](/pictures/dewiki/55/76db815eb80cddd85f88752074c15490.png)
![\sqrt[n]{a} \cdot \sqrt[m]{a} = \sqrt[n \cdot m]{a^{n+m}}](/pictures/dewiki/53/5c3f16f5ef7b5ba14e5e09590486d9aa.png)
![\frac{\sqrt[n]{a}}{\sqrt[m]{a}} = \sqrt[n \cdot m]{a^{m-n}}](/pictures/dewiki/99/c421793169cc0ac3780cc7cb4bad0129.png)
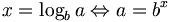
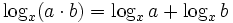
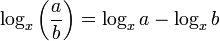
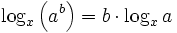
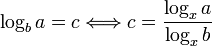
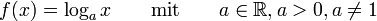
![\!\,D_f = ]0, + \infty[](/pictures/dewiki/99/c1b6a6325c0a55672b636cf9a2753f02.png)
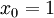
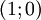
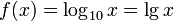
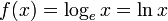
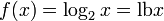

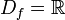
![\!\,W_f = ]0, + \infty[](/pictures/dewiki/56/8a2a336d9797ca4ca24d379f849d8127.png)
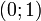
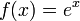
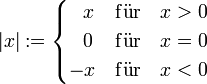
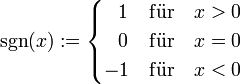
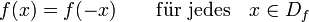
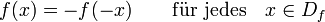

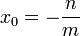
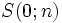
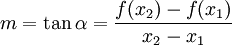
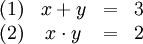
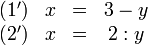

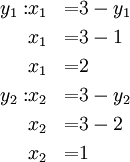
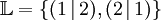
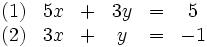
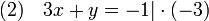
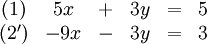
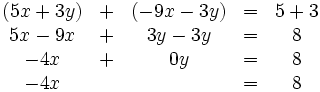
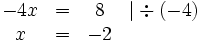
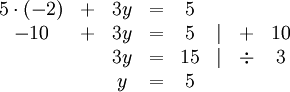
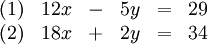
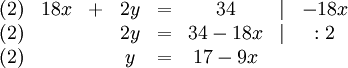
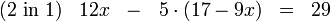
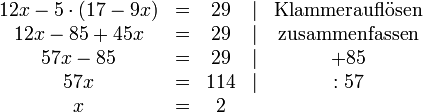

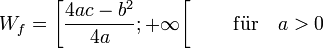
![\!\,W_f = \left]-\infty;\frac{4ac-b^2}{4a}\right] \qquad \mathrm{f\ddot ur}\quad a<0](/pictures/dewiki/99/c55f329e8b5df73716dc5bf88eebd1e4.png)
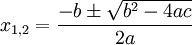
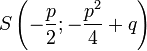
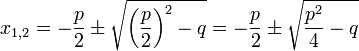
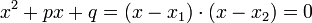
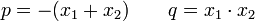
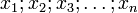
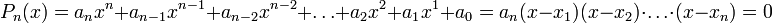
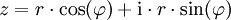
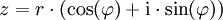
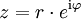
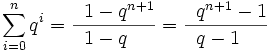 (
(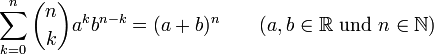 (
(