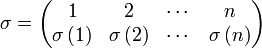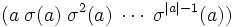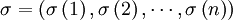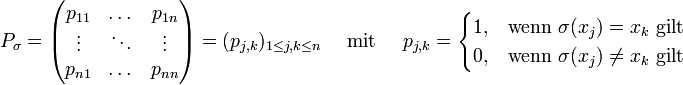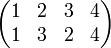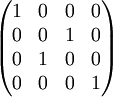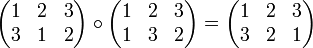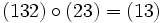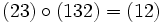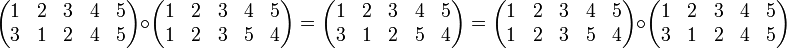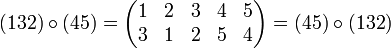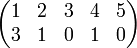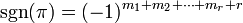Permutationsoperator

Unter einer Permutation (von lat. permutare „(ver)tauschen“) versteht man die Veränderung der Anordnung einer Menge durch Vertauschen ihrer Elemente. In der Mathematik ist eine Permutation eine bijektive Selbstabbildung einer in der Regel endlichen Menge. Umgangssprachlich findet der Begriff bisweilen auch als Synonym für „Anordnung“ Verwendung.

Beispiele

• „ANGSTBUDE“ entsteht aus „BUNDESTAG“ durch Permutation der Buchstaben (Anagramm).
• Das Mischen der Karten eines Kartenspiels ist eine Permutation auf der Menge der Karten.
• Der Stellungswechsel nach Eroberung des Aufschlagsrechts im Volleyball (rotieren) ist eine Permutation der Spieler.
• Sortieralgorithmen wie zum Beispiel der Bubble Sort arbeiten mit sukzessivem Vertauschen, d. h. mit der Hintereinanderausführung von speziellen Permutationen, sogenannten Transpositionen (siehe unten).

Formale Definition

Eine n-stellige Permutation ist eine bijektive Abbildung 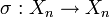$\sigma : X_n \rightarrow X_n$ einer n-elementigen Menge X_n auf sich selbst. Für eine n-elementigen Menge gibt es jeweils n! mögliche Permutationen. Die n-stelligen Permutationen der ersten n natürlichen Zahlen 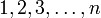$1, 2, 3, \ldots, n$ bilden die symmetrische Gruppe S_n (mit n! Elementen). Für die symmetrische Gruppe einer beliebigen Menge X_n schreibt man allgemein S(X_n).

Mathematische Schreibweisen und Darstellungen

Es gibt im Wesentlichen vier Arten zur Beschreibung einer n-stelligen Permutation: Matrixdarstellung, Zykelschreibweise, Tupelschreibweise und Permutationsmatrix. Im Folgenden bezeichnen wir die n Elemente von X_n mit 1,2,...,n und es sei $\sigma \in S_n$.

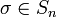Matrixdarstellung

In der ausführlichen Darstellung der Permutation σ schreibt man diese als 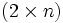$(2\times n)$-Matrix. In der oberen Zeile stehen die Elemente von X_n (in beliebiger Reihenfolge). Ist X_n = {1,..,n}, dann schreibt man im Allgemeinen die Zahlen von 1 bis n nacheinander in die erste Zeile. Unter jedes 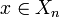$x\in X_n$ schreibt man in die zweite Zeile den Funktionswert σ(x). Auch in der zweiten Zeile steht somit jedes Element von X_n genau einmal.

$\sigma = \begin{pmatrix} 1 & 2 & \cdots & n \\ \sigma\left(1\right) & \sigma\left(2\right) & \cdots & \sigma\left(n\right) \end{pmatrix}$

Zykelschreibweise

Die Zykelschreibweise ist kompakter und benötigt nur eine Zeile. Wir beginnen mit einem beliebigen Element 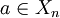$a\in X_n$ und schreiben

$(a \; \sigma(a) \; \sigma^2(a) \; \cdots \; \sigma^{|a|-1}(a))$

wobei σ^k die k-fache Hintereinanderausführung von σ bezeichnet und | a | die Elementordnung von a, das heißt | a | ist minimal mit σ ^{| a |} (a) = a bzw. σ ^{| a |} = ε. Eine solche Klammer heißt ein Zykel und | a | ist seine Länge. Gibt es weitere Elemente in X_n, die wir noch nicht notiert haben, so wählen wir ein solches Element b und schreiben eine weitere Klammer 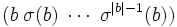$(b \; \sigma(b) \; \cdots \; \sigma^{|b|-1}(b))$. Wir fahren so lange fort, bis wir jedes Element genau einmal notiert haben. Klammern, in denen nur ein Element steht, können anschließend wieder gestrichen werden. Die Identität ε notiert man auch als leere Klammer ().

(124)(35) bedeutet beispielsweise, dass 1 auf 2, 2 auf 4 und 4 auf 1 abgebildet wird und zusätzlich 3 auf 5 und 5 auf 3.

Tupelschreibweise

Bei der Tupelschreibweise schreibt man die Funktionswerte σ(x) in eine Zeile.

$\sigma = \left(\sigma\left(1\right),\sigma\left(2\right),\cdots,\sigma\left(n\right)\right)$

Sie enthält somit nur noch die zweite Zeile der Matrixdarstellung. Da dadurch die Information über den x-Wert zu den σ(x) verloren geht, kann die Tupelschreibweise nur verwendet werden, wenn für die zugrundeliegende Menge eine Reihenfolge festgelegt wurde. An Hand dieser Reihenfolge lässt sich dann die erste Zeile der Matrixdarstellung rekonstruieren.

Die Tupelschreibweise wird leicht mit der Zykelschreibweise verwechselt, besonders da manche Autoren die Kommata weglassen.

Permutationsmatrix

Diese Darstellung ist nicht zu verwechseln mit der Matrixdarstellung. Bei dieser Darstellung wird ein Vektor von links mit einer Permutationsmatrix multipliziert, wodurch die Elemente des Vektors permutiert werden.

Definition

Sei 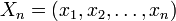$X_n=(x_1,x_2,\ldots,x_n)$ das n-Tupel und 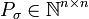$P_\sigma \in \mathbb{N}^{n\times n}$ die Permutationsmatrix.

Der Permutation 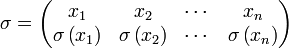$\sigma = \begin{pmatrix} x_1 & x_2 & \cdots & x_n \\ \sigma\left(x_1\right) & \sigma\left(x_2\right) & \cdots & \sigma\left(x_n\right) \end{pmatrix}$ entspricht dann die Matrix

$P_\sigma= \begin{pmatrix} p_{11} & \dots &p_{1n} \\ \vdots &\ddots &\vdots \\ p_{n1} & \dots &p_{nn} \end{pmatrix} = (p_{j,k})_{1\leq j,k \leq n} \quad\text{ mit }\quad p_{j,k}=\begin{cases} 1, & \text{wenn }\sigma(x_j)=x_k\text{ gilt } \\ 0, & \text{wenn } \sigma(x_j) \ne x_k\text{ gilt }\end{cases}$

Der Vektor 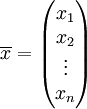$\overline{x} =\begin{pmatrix}x_1 \\ x_2 \\ \vdots \\ x_n \\\end{pmatrix}$ wird permutiert, indem man ihn von links mit P_σ multipliziert: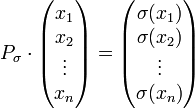 $P_\sigma \cdot \begin{pmatrix}x_1 \\ x_2 \\ \vdots \\ x_n \\\end{pmatrix} = \begin{pmatrix} \sigma(x_1) \\ \sigma(x_2) \\ \vdots \\ \sigma(x_n) \\\end{pmatrix}$

Bemerkung

Die identische Abbildung wird dargestellt durch die Einheitsmatrix .

Beispiele

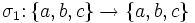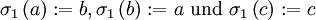• Ein einfaches Beispiel in verschiedenen Schreibweisen: Es sei $\sigma_1 \colon \{a,b,c \} \rightarrow \{a,b,c \}$ durch $\sigma_1\left(a\right):=b, \sigma_1\left(b\right):=a \mbox{ und } \sigma_1\left(c\right):=c$ gegeben. Dann gilt

Matrixdarstellung:	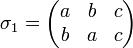$\sigma_1 = \begin{pmatrix} a & b & c \\ b & a & c \end{pmatrix}$
Zyklenschreibweise:	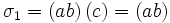$\sigma_1 = \left(a b\right)\left(c\right) = \left(a b\right)$ – a und b werden vertauscht, c wird gehalten
Tupelschreibweise:	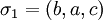$\sigma_1 = \left(b,a,c\right)$ oder auch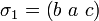 $\sigma_1 = \left(b\ a\ c\right)$
Permutationsmatrix:	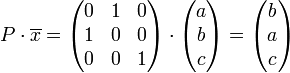$P \cdot \overline{x}= \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \cdot \begin{pmatrix}a \\ b \\ c \\\end{pmatrix} = \begin{pmatrix}b \\ a \\ c \\\end{pmatrix}$ – a und b werden vertauscht, c wird gehalten

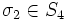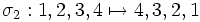• Ein weiteres Beispiel: Sei $\sigma_2 \in S_4$ durch $\sigma_2: 1, 2, 3, 4 \mapsto 4, 3, 2, 1$ gegeben. Dann schreibt man

Matrixdarstellung:	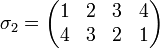$\sigma_2 = \begin{pmatrix} 1 & 2 & 3 & 4 \\ 4 & 3 & 2 & 1 \end{pmatrix}$
Zyklenschreibweise:	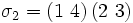$\sigma_2 = \left(1\ 4\right)\left(2\ 3\right)$
Tupelschreibweise:	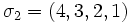$\sigma_2 = \left(4,3,2,1\right)$ oder auch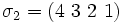 $\sigma_2 = \left(4\ 3\ 2\ 1\right)$
Permutationsmatrix:	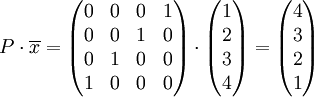$P \cdot \overline{x}= \begin{pmatrix} 0 & 0 & 0 & 1\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0\\ \end{pmatrix} \cdot \begin{pmatrix}1 \\ 2 \\ 3 \\ 4 \\\end{pmatrix} = \begin{pmatrix}4 \\ 3 \\ 2 \\ 1 \\\end{pmatrix}$

Keine der Darstellungen ist eindeutig.

Fixpunkte

Elemente, deren Positionen sich bei der Permutation nicht ändern, nennt man Fixpunkte der Permutation. Bei der Permutation

$\begin{pmatrix} 1 & 2 & 3 & 4 \\ 1 & 3 & 2 & 4 \end{pmatrix}$

sind dies beispielsweise die Zahlen 1 und 4. In der Matrixdarstellung erkennt man Fixpunkte daran, dass der obere und untere Eintrag der jeweiligen Spalte gleich ist. In der Zykelschreibweise sind Fixpunkte genau die Elemente, die nicht erscheinen. Für das obige Beispiel lautet die Zykelschreibweise (23); die Fixpunkte 1 und 4 erscheinen hier nicht. In der Permutationsmatrix sind die den Fixpunkten zugewiesenen Einträge der Hauptdiagonale 1. In der Permutationsmatrix zum obigen Beispiel sind dies die Einträge p_1,1 und p_4,4:

$\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}$

Verknüpfung von Permutationen, Symmetrische Gruppe

Zwei n-stellige Permutationen lassen sich nacheinander ausführen indem man die erste Permutation anwendet und auf deren Resultat dann die zweite Permutation. Diese Hintereinanderausführung wird auch Komposition, Verknüpfung oder Produkt zweier Permutationen genannt und ist selbst wieder eine n-stellige Permutation.

Die Menge der n-stelligen Permutationen bildet zusammen mit der Verknüpfung eine Gruppe: die Permutationsgruppe oder symmetrische Gruppe S_n. Ihr neutrales Element ist die Identität und zu jeder Permutation ist die inverse Permutation jeweils das inverse Element. Die symmetrischen Gruppen spielen in der Mathematik eine bedeutende Rolle. Beispielsweise ist jede endliche Gruppe zu einer Untergruppe einer symmetrischen Gruppe isomorph.

Beispiele zur Komposition von Permutationen

Beispiele zur Verknüpfung:

• $\begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{pmatrix} \circ \begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix} = \begin{pmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{pmatrix}$

Man beachte, dass die Verknüpfungen von rechts nach links ausgewertet werden (Manche Autoren werten jedoch auch von links nach rechts aus. [1]): In der zweiten Matrix geht die 1 in die 1, in der ersten die 1 in die 3. Im Ergebnis der Verknüpfung geht also die 1 in die 3. Ebenso: zweite Matrix 2 -> 3, erste Matrix 3 -> 2, Ergebnis 2 -> 2. Und: zweite Matrix 3 -> 2, erste Matrix 2 -> 1, Ergebnis 3 -> 1.

• $(132)\circ(23)=(1 3)$
• $(23)\circ(132)=(1 2)$

Die beiden letzten Beispiele zeigen, dass die Reihenfolge im Allgemeinen von Bedeutung ist: Die symmetrische Gruppe S_n ist für n > 2 nicht kommutativ. Die Reihenfolge kann nur unbeachtet bleiben, wenn die miteinander verknüpften Zykel disjunkt sind, d. h. jedes Element der Permutation kommt nur in einem Zykel vor. Beispiel:

• $\begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 3 & 1 & 2 & 4 & 5 \end{pmatrix} \circ \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 1 & 2 & 3 & 5 & 4 \end{pmatrix} = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 3 & 1 & 2 & 5 & 4 \end{pmatrix} = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 1 & 2 & 3 & 5 & 4 \end{pmatrix} \circ \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 3 & 1 & 2 & 4 & 5 \end{pmatrix}$

• $(132)\circ(45)= \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 3 & 1 & 2 & 5 & 4 \end{pmatrix} = (45) \circ(132)$

Spezielle Permutationen

Identität

Die Identität (abgekürzt id) ist diejenige Permutation, die alle Elemente an ihrem Platz belässt.

Transposition oder 2-Zykel

Eine Transposition ist eine Permutation, die genau zwei Elemente miteinander vertauscht.

Involution

Als Involution oder selbstinvers bezeichnet man eine Permutation π, bei der bei zweifacher Anwendung alle Elemente an ihrem Platz bleiben. Formal bedeutet dies π² = id. Eine Permutation ist genau dann eine Involution, wenn sie nur aus Fixpunkten und paarweise disjunkten Transpositionen besteht.

Derangement

Als Derangement bezeichnet man eine fixpunktfreie Permutation. Dies ist eine Permutation bei der kein einziges Element an seinem Platz bleibt.

Inverse Permutation

Zu jeder Permutation π gibt es eine Permutation π ^{− 1} mit 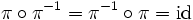$\pi \circ \pi^{-1} = \pi^{-1} \circ \pi = \mbox{id}$. Man nennt π ^{− 1} die zu π inverse Permutation. Man erhält diese aus der Zyklendarstellung von π, indem man das erste Element des Zyklus belässt und die restlichen Elemente umdreht, also in umgekehrter Reihenfolge aufschreibt.

Gerade Permutation

Eine Permutation heißt gerade, wenn sie Komposition einer geraden Anzahl von 2-Zykeln ist (siehe Signum und weiter unten).

Einige Eigenschaften von Permutationen

• Jede Permutation ist Komposition von 2-Zykeln.
• Die Anzahl der Permutationen auf einer Menge mit n Elementen ist genau n!.
• Ordnung: Für jede Permutation π gibt es eine kleinste natürliche Zahl k derart, dass π^k = id gilt. Diese Zahl ist die Ordnung von π als Gruppenelement der Symmetrischen Gruppe. Die Ordnung ist das kleinste gemeinsame Vielfache der Längen der Zyklen von π und damit ein Teiler der Gruppenordnung der Symmetrischen Gruppe. Besteht eine Permutation z. B. aus einem Zyklus der Länge 2 und einem Zyklus der Länge 3, so ist ihre Ordnung 6.
• „left-to-right maximum“ (Links-Rechts Maximum, kurz: LR-Maximum). Bei einer Permutation in Wortschreibweise 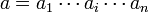$a = a_1 \cdots a_i \cdots a_n$ nennt man a_i ein LR-Maximum, genau dann wenn a_i > a_j mit 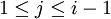$1 \leq j \leq i-1$. Diese Eigenschaft ist von Nutzen, wenn man die normalisierte Zyklendarstellung ohne Klammern schreiben möchte. Man kann unter Ausnutzung der LR-Maxima zeigen, dass dann eine Bijektion zwischen der normalisierten Zyklendarstellung in eine Permutation existiert.^[1] Bemerkung: a₁ ist immer ein LR-Maximum.
• Inversion/Fehlstand: Man nennt ein Paar (i,j) von Elementen Inversion bzgl. π, falls gilt

  i < j und 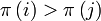$\pi\left(i\right) &amp;gt; \pi\left(j\right)$. Zwei Elemente bilden also genau dann eine Inversion, wenn nach Anwenden der Permutation das größere vor dem kleineren Element steht.

Beispiel: Gegeben sei die Permutation 32514. 1 < 2 aber 2 steht hier vor 1 also 1,2 sind eine Inversion bezüglich π.

Ordnet man in einer Tabelle jedem Element die Anzahl derjenigen Elemente zu, die nach der Permutation links von ihm stehen, obwohl sie größer sind, so erhält man die sogenannte Inversionstafel der Permutation. Umgekehrt kann man aus jeder solchen Tafel die Permutation eindeutig bestimmen.

Beispiel: Gegeben sei die Permutation 32514. Dann haben wir als Inversionstafel:

$\begin{pmatrix}1&amp;amp;2&amp;amp;3&amp;amp;4&amp;amp;5 \\ 3 &amp;amp; 1 &amp;amp; 0 &amp;amp; 1 &amp;amp; 0 \end{pmatrix}$

• Signum: Sei mit 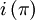$i\left(\pi\right)$ die Anzahl der Inversionen von π bezeichnet. Dann ist das Signum von π gegeben durch $\mathrm{sgn}\left(\pi\right) = \left(-1\right)^{i\left(\pi\right)}$.

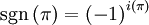Eine Permutation hat also Signum 1, falls die Anzahl ihrer Inversionen gerade ist, ansonsten Signum −1.

Das Signum lässt sich auch über folgende Formel bestimmen:

$\mathrm{sgn}(\pi) = (-1)^{m_1+m_2+\cdots+m_r+r}$

wobei r die Anzahl der Zyklen und m_i die Länge des i-ten Zyklus sind $\left(i=1,\ldots,r\right)$.

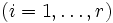• Typ: Sei mit b_i die Anzahl der Zyklen von π bezeichnet, welche die Länge i haben. Dann ist der Typ einer Permutation der formale Ausdruck

  $1^{b_1} 2^{b_2} 3^{b_3} \cdots n^{b_n}$.

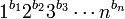Formal bedeutet hierbei, dass das Produkt und die Potenzen nicht tatsächlich ausgerechnet werden.

• Auf weitere Eigenschaften der Permutation und der Verkettung wird bei der Symmetrischen Gruppe eingegangen.

Siehe auch

• Permutiertes Register

Weblink

Literatur

• Albrecht Beutelspacher: Lineare Algebra. Kapitel 7.2 Permutationen, ISBN 3-528-56508-X.
• Michael Artin: Algebra. Kapitel 1.4 Permutationsmatrizen, ISBN 3-7643-2927-0.

Einzelnachweise

1. ↑ Vorlesungsskript Prof. Welker: Kapitel 1 & Kapitel 3 (PDF)