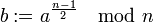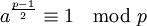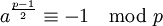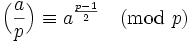Soloway-Strassen-Test

Der Solovay-Strassen-Test (nach Robert Solovay und Volker Strassen) ist ein probabilistischer Primzahltest. Der Test prüft für eine ungerade Zahl n, ob sie eine Primzahl oder das Produkt mehrerer Faktoren ist. Für den Fall, dass der Test als Antwort liefert, dass es sich bei n nicht um eine Primzahl handelt, liefert der Test jedoch im Allgemeinen keinen Faktor der Zahl n.

Der Test ist ein probabilistischer Algorithmus. Das heißt, er liefert nur mit einer gewissen Wahrscheinlichkeit (50%) eine Aussage. Durch Wiederholung kann diese Wahrscheinlichkeit aber beliebig vergrößert werden. Ergibt der Test (wiederholt) keine Aussage so lässt sich dies als n ist wahrscheinlich eine Primzahl interpretieren.

Der Test fällt in die Klasse der Monte-Carlo-Algorithmen d. h. für den Test wird ein Zufallsexperiment benötigt.

Er basiert ähnlich wie der Miller-Rabin-Test auf einer Eigenschaft, die Primzahlen betrifft.

Vorgehensweise

• Zu einer ungeraden Zahl n, welche auf Primzahleigenschaft zu testen ist, wird zufällig eine natürliche Zahl a mit 1 < a < n gewählt. Bei mehrfacher Durchführung des Tests sind für a jeweils neue Werte zu wählen.
• Es wird

g := ggT(a,n)

berechnet. Falls g > 1 gilt, so ist g ein echter Teiler von n. Damit ist n keine Primzahl und der Test wird beendet.

• berechne

$b := a^{\frac{n-1}{2}} \mod n$

Gilt 1 < b < n-1, so kann n nach dem Satz von Euler keine Primzahl sein und der Test wird beendet. Ist aber b = 1 oder b = n-1, kann es sich bei n um eine Eulersche Pseudoprimzahl handeln und der folgende Schritt muss noch ausgeführt werden.

• Berechne das Jacobi-Symbol

j := J(a,n)

Falls n eine Primzahl ist, so muss 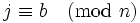$j\equiv b\pmod n$ gelten. Gilt dies nicht, kann n keine Primzahl sein und der Test ist beendet.

• Falls die Berechnungen nacheinander

g = 1

b = 1 oder b = n-1

j = b mod n

ergeben, liefert der Solovay-Strassen-Test keine Aussage, n ist also eventuell eine Primzahl.

Bewertung

Um die Güte des Solovay-Strassen-Tests zu bewerten, muss unterschieden werden, ob n eine Primzahl ist oder nicht.

• Falls n eine Primzahl ist, liefert der Test immer das korrekte Ergebnis.
• Falls n keine Primzahl ist, ist die Wahrscheinlichkeit, im ersten Schritt des Tests ein a zu wählen, sodass der Test ein falsches Ergebnis liefert, kleiner als 1/2 (siehe unten: Falsche Zeugen).

Um die Güte des Tests für Nichtprimzahlen zu erhöhen, wird der Test mit unabhängig gewählten zufälligen a-Werten hinreichend oft wiederholt. Wenn der Test k mal wiederholt wird, dann ist die Wahrscheinlichkeit, dass in allen k Wiederholungen das Ergebnis wahrscheinlich Primzahl lautet (obwohl n keine Primzahl ist), kleiner als 1 / 2^k. Dies ist eine pessimistische Schätzung - in den meisten Fällen wird die Güte wesentlich besser sein.

Effizienz

Der Solovay-Strassen-Test ist effizient, da der ggT, die Potenzen und das Jacobi-Symbol effizient berechnet werden können.

Beispiel

Am Beispiel der zusammengesetzten Zahl n = 91 (einer Pseudoprimzahl) werden die möglichen Abläufe des Tests gezeigt:

Ist 91 eine Primzahl?
Fall 1: a = 7	Fall 2: a=23	Fall 3: a= 17	Fall 4: a=29
g = ggT(7,91) = 7 => keine Primzahl	g = ggT(23,91) = 1 b = 23(91 − 1) / 2 mod 91 = 64 => keine Primzahl	g = ggT(17,91) = 1 b = 17(91 − 1) / 2 mod 91 = -1 j = J(17,91) = -1 j = b => Primzahl	g = ggT(29,91) = 1 b = 29(91 − 1) / 2 mod 91 = 1 j = J(29,91) = 1 j = b => Primzahl

Die Wahrscheinlichkeit an:

• Fall 1 zu scheitern beträgt bei 91 ca. 20%
• Fall 2 zu scheitern beträgt bei 91 ca. 61%

Falsche Zeugen

Sei n > 2 eine ungerade Nichtprimzahl. Eine Zahl a mit ggT(a,n) = 1 heißt falscher Zeuge für die Primalität von n bezüglich des Solovay-Strassen-Tests, falls

$a^{\frac{n-1}{2}} \equiv J(a,n) \pmod{n}$

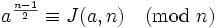
Die Menge der falschen Zeugen bildet eine Untergruppe zur multiplikativen Gruppe 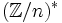$(\mathbb{Z}/n)^*$ mit Ordnung 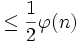$\leq \frac{1}{2}\varphi(n)$ (φ bezeichnet die Eulersche φ-Funktion).

Da φ(n) < n gilt, sind höchstens die Hälfte aller zur Auswahl stehenden Zahlen a falsche Zeugen.

Was steckt hinter dem Solovay-Strassen-Test?

Der Solovay-Strassen-Test beruht auf zwei Punkten:

• Das eine ist die Eigenschaft der Primzahl in Bezug auf den Eulerschen Satz:

Für jede Primzahl p > 2 gilt, dass entweder

• $a^{\frac{p-1}{2}} \equiv 1 \mod p$

oder

• $a^{\frac{p-1}{2}} \equiv -1 \mod p$

zutrifft.

Mit diesem Satz werden alle Zahlen herausgesiebt, die weder Primzahlen noch eulersche Pseudoprimzahlen zur Basis a sind.

• Das andere ist eine Eigenschaft, die oben genannter Satz mit dem Legendre-Symbol verbindet:

$\Big(\frac{a}{p}\Big) \equiv a^{\frac{p-1}{2}}\pmod p$

Da man bei den zu testenden Zahlen nicht davon ausgehen darf, dass es sich um Primzahlen handelt, benutzt man das Jacobi-Symbol. Damit fallen auch jene eulerschen Pseudoprimzahlen raus, für die $a^{\frac{n-1}{2}} \equiv \left(\frac{a}{n}\right) \mod n$ nicht gilt.