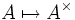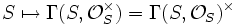- Multiplikative Gruppe
-
In der Mathematik ist die Einheitengruppe eines Rings mit Einselement die Menge aller multiplikativ invertierbaren Elemente. Sie ist mit der Ringmultiplikation eine Gruppe.
Besonders interessant sind die Einheitengruppen von (unitären) assoziativen Algebren. Diese können als eine Verallgemeinerung der allgemeinen linearen Gruppe angesehen werden.
Inhaltsverzeichnis
Definition
Sei R ein Ring mit 1. Die Menge aller multiplikativ invertierbaren Elemente (Einheiten) von R bildet mit der Ringmultiplikation eine Gruppe. Sie wird Einheitengruppe von R genannt. Man schreibt die Einheitengruppe meist als R * oder als
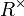 .
.Eigenschaften und verwandte Begriffe
- Ein kommutativer Ring mit 1, dessen Einheitengruppe aus allen Elementen außer der Null besteht, ist bereits ein Körper.
- Ist das Komplement der Einheitengruppe ein Ideal, dann nennt man den Ring lokal.
Beispiele
Die Einheitengruppe des Rings
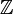 der ganzen Zahlen besteht aus den beiden Elementen 1 und -1.
der ganzen Zahlen besteht aus den beiden Elementen 1 und -1.Die Einheitengruppe des Rings
 der rationalen Zahlen besteht aus allen rationalen Zahlen ungleich der Null,
der rationalen Zahlen besteht aus allen rationalen Zahlen ungleich der Null,  ist also ein Körper.
ist also ein Körper.Die Einheitengruppe des Restklassenrings modulo 10 besteht aus den Elementen 1, 3, 7 und 9.
Die Einheitengruppe des Matrizenrings der
 -Matrizen mit Koeffizienten in einem Körper K heißt allgemeine lineare Gruppe GL(n,K).
-Matrizen mit Koeffizienten in einem Körper K heißt allgemeine lineare Gruppe GL(n,K). 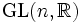 und
und 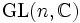 sind Lie-Gruppen.
sind Lie-Gruppen.Die multiplikative Gruppe als algebraische Gruppe
Als multiplikative Gruppe wird auch die zugehörige algebraische Gruppe bezeichnet:
- In der Sprache der Varietäten ist die multiplikative Gruppe über einem algebraisch abgeschlossenen Körper k die affine Varietät
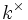 mit der Körpermultiplikation als Gruppenoperation.
mit der Körpermultiplikation als Gruppenoperation. - In der Sprache der Schemata ist die multiplikative Gruppe das Schema
![\operatorname{Spec}\mathbb Z[T,T^{-1}]](/pictures/dewiki/99/cce74ac7489390425e40d25258e34672.png) mit der Komultiplikation
mit der Komultiplikation 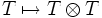 ; die multiplikative Gruppe über anderen Schemata erhält man durch Basiswechsel.
; die multiplikative Gruppe über anderen Schemata erhält man durch Basiswechsel. - In der Sprache der Gruppenfunktoren ist die multiplikative Gruppe der Funktor
-
- für Ringe A bzw.
- für Schemata S.
Die multiplikative Gruppe wird mit dem Symbol
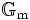 oder mit GL1 bezeichnet; sie ist ein Spezialfall der allgemeinen linearen Gruppe.
oder mit GL1 bezeichnet; sie ist ein Spezialfall der allgemeinen linearen Gruppe.Weblinks
Wikimedia Foundation.