Eulersche φ-Funktion

Die ersten tausend Werte von φ(n)

Die eulersche φ-Funktion (auch eulersche Funktion genannt) ist eine zahlentheoretische Funktion. Sie gibt für jede natürliche Zahl n an, wie viele positive ganze Zahlen $a \le n$ zu ihr teilerfremd sind:

$\varphi(n) \; := \; \Big| \{ 1 \le a \le n \, |\, \operatorname{ggT}(a,n) = 1 \} \Big|$

Dabei bezeichnet $\operatorname{ggT}(a,n)$ den größten gemeinsamen Teiler von a und n.

Die φ-Funktion ist benannt nach Leonhard Euler und wird mit dem griechischen Buchstaben Phi bezeichnet.

Beispiele

Die ersten 100 Werte der φ-Funktion

• Die Zahl 6 ist zu zwei der Zahlen von 1 bis 6 teilerfremd (1 und 5), also ist φ(6) = 2.
• Die Zahl 13 ist als Primzahl zu den zwölf Zahlen 1 bis 12 teilerfremd, also ist φ(13) = 12.

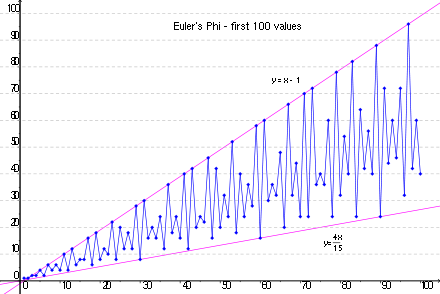
Die ersten 99 Werte der φ-Funktion lauten:

φ(n)	+0	+1	+2	+3	+4	+5	+6	+7	+8	+9
0+		1	1	2	2	4	2	6	4	6
10+	4	10	4	12	6	8	8	16	6	18
20+	8	12	10	22	8	20	12	18	12	28
30+	8	30	16	20	16	24	12	36	18	24
40+	16	40	12	42	20	24	22	46	16	42
50+	20	32	24	52	18	40	24	36	28	58
60+	16	60	30	36	32	48	20	66	32	44
70+	24	70	24	72	36	40	36	60	24	78
80+	32	54	40	82	24	64	42	56	40	88
90+	24	72	44	60	46	72	32	96	42	60

Eigenschaften

Multiplikative Funktion

Die φ-Funktion ist eine multiplikative zahlentheoretische Funktion, so dass gilt

$\varphi (m \cdot n) = \varphi (m) \cdot \varphi (n)$, sofern m und n teilerfremd sind.

Beispiel:

$\varphi(18) = \varphi(2)\cdot\varphi(9) = 1\cdot 6 = 6$

Dichte

Die Funktion $\varphi(n)\,$ gibt die Anzahl der Einheiten im Restklassenring $\Bbb{Z}/n\Bbb{Z}$ an.

Denn ist $\overline{a}\in\Bbb{Z}/n\Bbb{Z}$ eine Einheit, also $\overline{a}\in(\Bbb{Z}/n\Bbb{Z})^*$, so gibt es ein $\overline{b}\in\Bbb{Z}/n\Bbb{Z}$ mit $\overline{a}\cdot\overline{b}=\overline{1}$.

Was äquivalent zu $ab\equiv 1 \, \mathrm{mod} \, n$ und $ab+nx=1\,$ ist, wenn man $x\in\Bbb{Z}$ geeignet wählt.

Nach dem Lemma von Bézout ist dies äquivalent zur Teilerfremdheit von $a\,$ und $n\,$.

φ(n) ist für n > 2 stets eine gerade Zahl.

Ist a_n die Anzahl der Elemente aus dem Bild im(φ), die kleinergleich n sind, dann gilt $\lim_{n\to\infty} \frac{a_n}{n}=0$.

Das Bild der φ-Funktion besitzt also die natürliche Dichte 0.

Berechnung

Primzahlen

Da jede Primzahl p nur durch 1 und sich selbst teilbar ist, ist sie zu den Zahlen 1 bis p − 1 teilerfremd. Es gilt daher

φ(p) = p − 1

Potenz von Primzahlen

Eine Potenz p^k mit einer Primzahl p als Basis und einer natürlichen Zahl k als Exponent hat mit p nur einen Primfaktor. Infolgedessen hat p^k nur mit Vielfachen von p einen von eins verschiedenen gemeinsamen Teiler. Im Bereich von 1 bis p^k sind das die Zahlen

$1\cdot p, 2\cdot p, 3\cdot p, \cdots, p^{k-1} \cdot p = p^k$

Das sind p^{k − 1} Zahlen, die nicht teilerfremd zu p^k sind. Für die eulersche φ-Funktion gilt deshalb die Formel

$\varphi(p^k) = p^k-p^{k-1} = p^{k-1}(p-1)= p^{k}\left(1-\frac1{p}\right)$

Beispiel:

$\varphi(16)=\varphi(2^4)=2^4-2^3=2^3\cdot (2-1)=2^4\cdot \left(1-\frac12\right) =8$

Allgemeine Berechnungsformel

Der Wert der eulerschen φ-Funktion lässt sich für jede Zahl aus ihrer kanonischen Primfaktorzerlegung

$n = \prod_{p\mid n} p^{k_p}$

berechnen:

$\varphi(n) = \prod_{p\mid n} p^{k_p-1}(p-1) = n \prod_{p\mid n}\left(1-\frac{1}{p}\right)$

Diese Formel folgt direkt aus der Multiplikativität der φ-Funktion und der Formel für Primzahlpotenzen.

Beispiel:

$\varphi(72)=\varphi(2^3\cdot 3^2)=2^{3-1}\cdot (2-1)\cdot 3^{2-1}\cdot (3-1)=2^2\cdot 1\cdot 3\cdot 2=24$

Abschätzung

Eine Abschätzung für das arithmetische Mittel von φ(n) erhält man über die Formel

$\sum_{n=1}^N \varphi(n) = \frac{1}{2 \zeta(2)} N^2 + \mathcal{O}(N \log N)$,

wobei ζ die riemannsche Zetafunktion und O das Landau-Symbol ist.

Das heißt: Im Mittel ist $\varphi(n) \approx n\frac{3}{\pi^2}.$

Weitere Beziehungen

Für $n \geq 2$ gilt:

$\sum_{1 \leq j \leq n-1 \atop (n,j)=1} j = \frac{n}{2} \varphi(n)$

Bedeutung

Eine der wichtigsten Anwendungen findet die φ-Funktion im Satz von Fermat-Euler:

Wenn zwei ganze Zahlen a und m ≥ 2 teilerfremd sind, gilt:

$m \mid a^{\varphi(m)}-1$ (m teilt a hoch Phi von m minus 1),

oder anders formuliert:

$a^{\varphi(m)} \equiv 1 \pmod m$

Ein Spezialfall (für Primzahlen p) dieses Satzes ist der kleine fermatsche Satz:

$p \mid a^{p-1}-1$,

bzw.

$a^{p-1} \equiv 1 \pmod p$

Der Satz von Fermat-Euler findet unter anderem Anwendung bei der Generierung von Schlüsseln für das RSA-Verfahren in der Kryptographie.

Weblinks

• Die ersten 100000 Werte der φ-Funktion
• Programme zur φ-Funktion
• Folge der Funktionswerte φ(n): Folge A000010 in OEIS