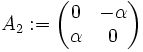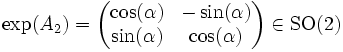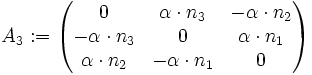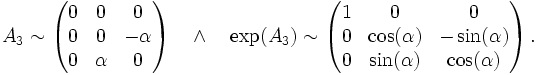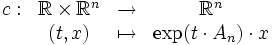- Spezielle orthogonale Gruppe
-
Die spezielle orthogonale Gruppe
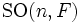 ist die Gruppe aller orthogonalen
ist die Gruppe aller orthogonalen 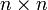 -Matrizen mit Koeffizienten aus einem Körper F mit Determinante Eins:
-Matrizen mit Koeffizienten aus einem Körper F mit Determinante Eins:Hierbei ist mit
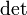 die Determinante und mit En die Einheitsmatrix gemeint. Wenn aus dem Kontext klar ist, welcher Körper F ist, schreibt man auch
die Determinante und mit En die Einheitsmatrix gemeint. Wenn aus dem Kontext klar ist, welcher Körper F ist, schreibt man auch  . Die Gruppe ist im Allgemeinen nicht kommutativ.
. Die Gruppe ist im Allgemeinen nicht kommutativ.Inhaltsverzeichnis
Die SO als Untergruppe
Die spezielle orthogonale Gruppe
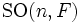 ist Untergruppe
ist Untergruppe- der orthogonalen Gruppe
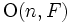
- der speziellen linearen Gruppe
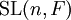 und
und - der allgemeinen linearen Gruppe
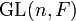 .
.
Wenn F die Charakteristik 2 hat, fallen
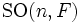 und
und 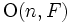 zusammen.
zusammen.Reelle spezielle orthogonale Gruppen
Die spezielle orthogonale Gruppe
 über dem Körper
über dem Körper 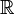 der reellen Zahlen beschreiben Drehungen im Euklidischen Raum
der reellen Zahlen beschreiben Drehungen im Euklidischen Raum 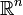 . Daher bezeichnet man die Gruppe
. Daher bezeichnet man die Gruppe  auch als Drehgruppe.
auch als Drehgruppe.  bildet eine reelle kompakte zusammenhängende Lie-Gruppe der Dimension
bildet eine reelle kompakte zusammenhängende Lie-Gruppe der Dimension 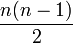 . Die Lie-Algebra der
. Die Lie-Algebra der  besteht aus dem Raum
besteht aus dem Raum 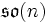 der schiefsymmetrischen reellen Matrizen.
der schiefsymmetrischen reellen Matrizen.Reelle orthogonale Gruppe SO(2)
Sei die schiefsymmetrische Matrix
mit den Eigenwerten
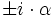 gegeben. Dann beschreibt der Endomorphismus A2 eine Multiplikation mit
gegeben. Dann beschreibt der Endomorphismus A2 eine Multiplikation mit  in den komplexen Zahlen
in den komplexen Zahlen 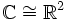 . Außerdem beschreibt
. Außerdem beschreibtgerade die Rotation um den Winkel
 .
.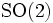 ist daher isomorph zum Einheitskreis
ist daher isomorph zum Einheitskreis 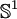 in der Ebene der komplexen Zahlen mit der komplexen Multiplikation als Verknüpfung.
in der Ebene der komplexen Zahlen mit der komplexen Multiplikation als Verknüpfung.Reelle orthogonale Gruppe SO(3)
Sei die schiefsymmetrische Matrix
mit
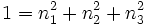 gegeben. Dann ist
gegeben. Dann ist 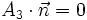 und für die Matrizen A3 und exp(A3) gelten folgende Ähnlichkeiten
und für die Matrizen A3 und exp(A3) gelten folgende ÄhnlichkeitenHierbei wurde eine Orthonormalbasis gewählt, bei der der erste Vektor gerade
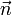 ist. exp(A3) beschreibt also eine Drehung des Winkels α um die Drehachse
ist. exp(A3) beschreibt also eine Drehung des Winkels α um die Drehachse 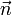 .
. ist lokal, aber nicht global isomorph zur speziellen unitären Gruppe
ist lokal, aber nicht global isomorph zur speziellen unitären Gruppe  , ablesbar an isomorphen Lie-Algebren. Zu den verschiedenen Parametrisierungen der
, ablesbar an isomorphen Lie-Algebren. Zu den verschiedenen Parametrisierungen der  siehe Eulersche Winkel.
siehe Eulersche Winkel.Vektorfelder von gleichmäßigen reellen Rotationen
Jede Rotation im
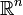 lässt sich mit Hilfe einer schiefsymmetrischen Matrix
lässt sich mit Hilfe einer schiefsymmetrischen Matrix 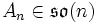 als Funktion c(t,x) = exp(An)tx beschreiben. Hierbei ist t der Zeitpunkt und x der Ausgangsort der Bewegung.
als Funktion c(t,x) = exp(An)tx beschreiben. Hierbei ist t der Zeitpunkt und x der Ausgangsort der Bewegung.Wegen
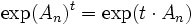 bedeutet das also
bedeutet das alsoAls entsprechendes Vektorfeld
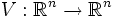 erhält man dann
erhält man dannVektorfelder von gleichmäßigen Rotationen lassen sich also gerade durch schiefsymmetrische Matrizen darstellen.
Wikimedia Foundation.