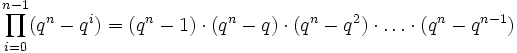- Projektive lineare Gruppe
-
Allgemeine lineare Gruppe GL(n,K) berührt die Spezialgebiete
ist Spezialfall von
- Gruppe
- unendliche Gruppe
umfasst als Spezialfälle
Die allgemeine lineare Gruppe GL(n,K) vom Grad n über einem Körper K ist die Gruppe aller invertierbaren
 -Matrizen mit Koeffizienten aus K. Gruppenverknüpfung ist die Matrixmultiplikation. Die Bezeichnung GL kommt von der Abkürzung der englischen Bezeichnung „general linear group“.
-Matrizen mit Koeffizienten aus K. Gruppenverknüpfung ist die Matrixmultiplikation. Die Bezeichnung GL kommt von der Abkürzung der englischen Bezeichnung „general linear group“.Wenn der Körper K ein endlicher Körper
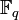 mit einer Primzahlpotenz q = pm ist, so schreibt man auch GL(n,q) statt GL(n,K). Wenn aus dem Kontext klar ist, dass der Körper
mit einer Primzahlpotenz q = pm ist, so schreibt man auch GL(n,q) statt GL(n,K). Wenn aus dem Kontext klar ist, dass der Körper  der reellen oder
der reellen oder  der komplexen Zahlen zu Grunde gelegt ist, schreibt man auch GL(n) oder GLn.
der komplexen Zahlen zu Grunde gelegt ist, schreibt man auch GL(n) oder GLn.Die allgemeine lineare Gruppe und ihre Untergruppen finden Anwendung in der Darstellung von Gruppen sowie in der Untersuchung von Symmetrien.
Inhaltsverzeichnis
Allgemeine lineare Gruppe über einem Vektorraum
Wenn V ein Vektorraum über einem Körper K ist, schreibt man GL(V) oder Aut(V) für die Gruppe aller Automorphismen von V, also aller bijektiven linearen Abbildungen
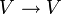 , mit der Hintereinanderausführung solcher Abbildungen als Gruppenverknüpfung.
, mit der Hintereinanderausführung solcher Abbildungen als Gruppenverknüpfung.Wenn V die endliche Dimension n hat, sind GL(V) und GL(n,K) isomorph. Für eine gegebene Basis des Vektorraums V kann jeder Automorphismus von V durch eine invertierbare
 -Matrix dargestellt werden. Dadurch wird ein Isomorphismus von GL(V) auf GL(n,K) hergestellt.
-Matrix dargestellt werden. Dadurch wird ein Isomorphismus von GL(V) auf GL(n,K) hergestellt.Für
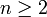 ist die Gruppe GL(n,K) nicht abelsch.
ist die Gruppe GL(n,K) nicht abelsch.Das Zentrum von GL(n,K) besteht gerade aus den Vielfachen der Einheitsmatrix (mit Skalaren aus K / {0}).
Untergruppen von GL(n,K)
Jede Untergruppe von GL(n,K) wird eine lineare Gruppe genannt. Einige Untergruppen haben besondere Bedeutung.
Die Untergruppe aller diagonalen Matrizen beschreibt Reskalierungen des Raums.
Die spezielle lineare Gruppe SL(n,K) enthält alle Matrizen mit der Determinante 1. SL(n,K) ist eine normale Untergruppe von GL(n,K); und die Faktorgruppe GL(n,K) / SL(n,K) ist isomorph zu
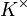 , der multiplikativen Gruppe von K (ohne die 0).
, der multiplikativen Gruppe von K (ohne die 0).Die orthogonale Gruppe O(n,K) enthält alle orthogonalen Matrizen. Für
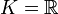 beschreiben diese Matrizen Automorphismen des
beschreiben diese Matrizen Automorphismen des  , die die Euklidische Norm und das Skalarprodukt erhalten, also orthogonale Abbildungen.
, die die Euklidische Norm und das Skalarprodukt erhalten, also orthogonale Abbildungen.Über
 und
und 
Die allgemeine lineare Gruppe GL(n) über dem Körper
 oder
oder  ist eine Lie-Gruppe über dem Körper und hat die Dimension n2.
ist eine Lie-Gruppe über dem Körper und hat die Dimension n2.- Beweis:
- GL(n) ist eine Untermenge der Mannigfaltigkeit Matn(K) aller
 -Matrizen, die ein Vektorraum der Dimension n2 ist. Die Determinante ist eine stetige (sogar polynomiale) Abbildung
-Matrizen, die ein Vektorraum der Dimension n2 ist. Die Determinante ist eine stetige (sogar polynomiale) Abbildung 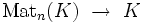 . GL(n) ist als Urbild der offenen Teilmenge
. GL(n) ist als Urbild der offenen Teilmenge 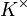 von K eine offene, nicht leere Teilmenge von Matn(K) und hat deshalb die gleiche Dimension.
von K eine offene, nicht leere Teilmenge von Matn(K) und hat deshalb die gleiche Dimension.
- GL(n) ist eine Untermenge der Mannigfaltigkeit Matn(K) aller
Die Lie-Algebra zu GL(n) ist die Allgemeine lineare Lie-Algebra gl(n) und sie besteht aus allen
 -Matrizen mit dem Kommutator als Lie-Klammer.
-Matrizen mit dem Kommutator als Lie-Klammer.Während
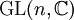 zusammenhängend ist, hat
zusammenhängend ist, hat 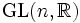 zwei Zusammenhangskomponenten: die Matrizen mit positiver und die mit negativer Determinante. Die Zusammenhangskomponente mit positiver Determinante enthält das Einselement und bildet eine Untergruppe
zwei Zusammenhangskomponenten: die Matrizen mit positiver und die mit negativer Determinante. Die Zusammenhangskomponente mit positiver Determinante enthält das Einselement und bildet eine Untergruppe 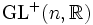 . Diese Untergruppe ist eine zusammenhängende Lie-Gruppe mit reeller Dimension n2 und hat dieselbe Lie-Algebra wie
. Diese Untergruppe ist eine zusammenhängende Lie-Gruppe mit reeller Dimension n2 und hat dieselbe Lie-Algebra wie 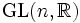 .
.Über endlichen Körpern
Wenn K ein endlicher Körper mit q Elementen ist, dann ist GL(n,K) eine endliche Gruppe der Ordnung
Dieser Wert kann beispielsweise durch Abzählen der Möglichkeiten für die Matrixspalten ermittelt werden: Für die erste Spalte gibt es qn − 1 Belegungsmöglichkeiten (alle außer der Nullspalte), für die zweite Spalte gibt es qn − q Möglichkeiten (alle außer den Vielfachen der ersten Spalte), etc.
Projektive lineare Gruppe
Die projektive lineare Gruppe PGL(V) über einem Vektorraum V über einem Körper K ist die Faktorgruppe
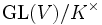 , wobei
, wobei 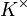 die normale Untergruppe der skalaren Vielfachen
die normale Untergruppe der skalaren Vielfachen 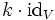 der Identität
der Identität 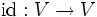 ist mit k aus
ist mit k aus 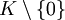 . Die Bezeichnungen PGL(n,K) usw. entsprechen denen der allgemeinen linearen Gruppe. Wenn K ein endlicher Körper ist, sind PGL(n,K) und SL(n,K) gleichmächtig, aber im allgemeinen nicht isomorph.
. Die Bezeichnungen PGL(n,K) usw. entsprechen denen der allgemeinen linearen Gruppe. Wenn K ein endlicher Körper ist, sind PGL(n,K) und SL(n,K) gleichmächtig, aber im allgemeinen nicht isomorph.Der Name stammt aus der projektiven Geometrie, wo das Analogon zur allgemeinen linearen Gruppe die projektive lineare Gruppe ist, zum n-dimensionalen projektiven Raum über K gehört dabei die Gruppe PGL(n + 1,K). Dies ist eine Verallgemeinerung der Gruppe der Möbius-Transformationen, der
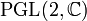 .
. - Gruppe
Wikimedia Foundation.