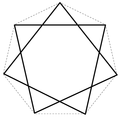
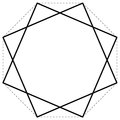
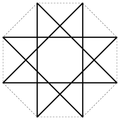
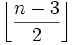Isogon — verschiedene Polygone bzw. polygonale Flächen Polygon (v. griech.: polýs = viel + gonía = Winkel) oder auch Vieleck ist ein Begriff aus der Geometrie und dabei insbesondere der Planimetrie. Ein Polygon erhält man, indem man mindestens drei… … Deutsch Wikipedia
N-Eck — verschiedene Polygone bzw. polygonale Flächen Polygon (v. griech.: polýs = viel + gonía = Winkel) oder auch Vieleck ist ein Begriff aus der Geometrie und dabei insbesondere der Planimetrie. Ein Polygon erhält man, indem man mindestens drei… … Deutsch Wikipedia
N-eck — verschiedene Polygone bzw. polygonale Flächen Polygon (v. griech.: polýs = viel + gonía = Winkel) oder auch Vieleck ist ein Begriff aus der Geometrie und dabei insbesondere der Planimetrie. Ein Polygon erhält man, indem man mindestens drei… … Deutsch Wikipedia
Polygonal — verschiedene Polygone bzw. polygonale Flächen Polygon (v. griech.: polýs = viel + gonía = Winkel) oder auch Vieleck ist ein Begriff aus der Geometrie und dabei insbesondere der Planimetrie. Ein Polygon erhält man, indem man mindestens drei… … Deutsch Wikipedia
Regelmäßiges Polygon — verschiedene Polygone bzw. polygonale Flächen Polygon (v. griech.: polýs = viel + gonía = Winkel) oder auch Vieleck ist ein Begriff aus der Geometrie und dabei insbesondere der Planimetrie. Ein Polygon erhält man, indem man mindestens drei… … Deutsch Wikipedia
Regelmäßiges Vieleck — verschiedene Polygone bzw. polygonale Flächen Polygon (v. griech.: polýs = viel + gonía = Winkel) oder auch Vieleck ist ein Begriff aus der Geometrie und dabei insbesondere der Planimetrie. Ein Polygon erhält man, indem man mindestens drei… … Deutsch Wikipedia
Reguläres Vieleck — verschiedene Polygone bzw. polygonale Flächen Polygon (v. griech.: polýs = viel + gonía = Winkel) oder auch Vieleck ist ein Begriff aus der Geometrie und dabei insbesondere der Planimetrie. Ein Polygon erhält man, indem man mindestens drei… … Deutsch Wikipedia
Vieleck — verschiedene Polygone bzw. polygonale Flächen Polygon (v. griech.: polýs = viel + gonía = Winkel) oder auch Vieleck ist ein Begriff aus der Geometrie und dabei insbesondere der Planimetrie. Ein Polygon erhält man, indem man mindestens drei… … Deutsch Wikipedia
Zwölfeck — verschiedene Polygone bzw. polygonale Flächen Polygon (v. griech.: polýs = viel + gonía = Winkel) oder auch Vieleck ist ein Begriff aus der Geometrie und dabei insbesondere der Planimetrie. Ein Polygon erhält man, indem man mindestens drei… … Deutsch Wikipedia