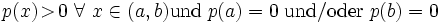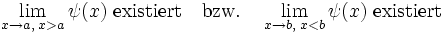- Sturm-Liouville-Operator
-
In der Analysis handelt es sich bei dem Sturm-Liouville-Problem (nach Joseph Liouville und Charles-François Sturm) um ein spezielles Randwertproblem, welches mit Methoden der Variationsrechnung behandelt werden kann. Dadurch ist es möglich, die Lösungen mittels eines linearen Integraloperators darzustellen, der eine Greensche Funktion des Problems als Kern hat.
Differentialgleichungen der Form
sind dem verallgemeinerten Eigenwertproblem
äquivalent, worin
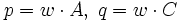 gesetzt ist und w(x) eine exponentielle Gewichtsfunktion ist, d.h. auf dem Definitionsintervall streng positiv ist.
gesetzt ist und w(x) eine exponentielle Gewichtsfunktion ist, d.h. auf dem Definitionsintervall streng positiv ist.lineare Operatoren der Form
werden Sturm-Liouville-Operatoren genannt.
Inhaltsverzeichnis
Reguläre Sturm-Liouville-Probleme
Die Eigenwertgleichung
mit glatten reellen Funktionen p(x),q(x),w(x) zusammen mit Randbedingungen der Form
(mit
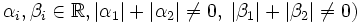 nennt man ein „reguläres Sturm-Liouville-Problem“ über dem Intervall [a,b], wenn dieses Intervall endlich ist und
nennt man ein „reguläres Sturm-Liouville-Problem“ über dem Intervall [a,b], wenn dieses Intervall endlich ist undgilt.
Singuläre Sturm-Liouville-Probleme
Ist das Intervall unendlich oder gilt
oder verschwindet das Gewicht w(x) an einigen Punkten oder ersetzt man eine oder beide der Randbedingungen durch
(oder einer ähnlichen Bedingung), so spricht man von einem „singulären Sturm-Liouville-Problem“.
Eigenschaften und Anwendungen
siehe Kai Gehrs, Sturm-Liouville-Probleme
Literatur
Weidmann, Joachim: Lineare Operatoren in Hilberträumen / Teil 2. Anwendungen. 1. Aufl. Auflage. Teubner, Stuttgart; Leipzig; Wiesbaden 2003, ISBN 3-519-02237-0.
Wikimedia Foundation.

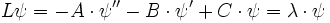
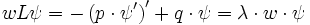
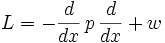
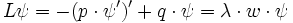
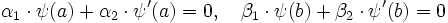
![p(x)\!>\!0\ \forall\ x \in [a,b] \quad \mathrm{sowie} \quad w(x)\!>\!0\ \forall\ x \in [a,b]](/pictures/dewiki/102/ffa51c65eaf2aeebc84d23aa9f823f4a.png)