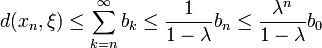Banachscher Fixpunktsatz

Der Fixpunktsatz von Banach ist ein Satz aus der Mathematik. Er ist nach dem Mathematiker Stefan Banach benannt und enthält eine Existenz-, eine Konstruktions- und eine Fehleraussage für Fixpunktprobleme.

Eine Veranschaulichung des Satzes liefert eine Landkarte, auf der die Umgebung, in der man sich befindet, abgebildet ist. Sieht man diese Karte als Kontraktion der Umgebung, so findet man genau einen Punkt auf der Karte, der mit dem direkt darunter liegenden Punkt in der realen Welt übereinstimmt.

Aussagen des Fixpunktsatzes

Existenz und Eindeutigkeit: Eine Kontraktion 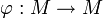$\varphi: M \to M$ eines (nichtleeren) vollständigen metrischen Raumes M besitzt genau einen Fixpunkt, also einen Punkt 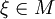$\xi \in M$ mit $\varphi(\xi) = \xi$.

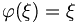Dabei ist:

• zum Beispiel jeder Banachraum, und unter diesen jeder normierte endlichdimensionale reelle oder komplexe Vektorraum, ein vollständiger metrischer Raum,
• eine Kontraktion eine Abbildung 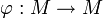$\varphi: M \to M$, welche Lipschitz-stetig mit einer Konstanten 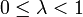$0\leq\lambda<1$ ist.

Konstruktion: Für jeden Startwert 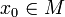$x_0 \in M$ konvergiert die Folge (x_n) mit 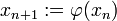$x_{n+1} := \varphi(x_n)$ gegen ξ.

Fehlerabschätzung: Es gibt die folgenden Abschätzungen für den Abstand des Fixpunktes zur rekursiven Folge:

• A-priori-Abschätzung

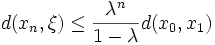$d(x_n,\xi)\le\frac{\lambda^n}{1-\lambda}d(x_0,x_1)$ (u.a. auch für n=0)

für den n-ten Fehler durch die ersten beiden Folgenglieder und die

• A-posteriori-Abschätzung

$d(x_n,\xi)\le\frac{\lambda}{1-\lambda}d(x_{n-1},x_n)$

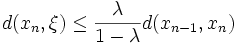
für den n-ten Fehler durch die beiden zuletzt bestimmten Folgenglieder.

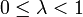$0\leq\lambda<1$ ist dabei die Kontraktionskonstante bzw. Lipschitz-Konstante.

Bemerkung: Oft wird dieser Satz nicht allgemein auf (vollständigen) metrischen Räumen, sondern auf einem Banach-Raum B, also einem vollständigen normierten Vektorraum, oder einer Teilmenge M⊆B davon formuliert. Der einzige Unterschied ist, dass der Abstand dann durch die Norm der Differenz erklärt ist, $d(x,y):=\|y-x\|$.

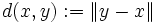Zum Beweis

Beweisidee für normierte Räume

Um den Beweisgang zu verstehen, ist es hilfreich, zunächst in einem Banach-Raum zu operieren. Die eigentlichen Beweisschritte können dann auch im metrischen Raum vollzogen werden. Wir konstruieren die rekursive Folge 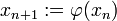$x_{n+1} := \varphi(x_n)$ mit irgendeinem Startpunkt 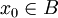$x_0\in B$. Diese fassen wir als Partialsummen einer (Teleskop-)Reihe auf, deren Glieder die Differenzen 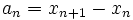$a_n=x_{n+1}-x_n\,$ sind, $x_n-x_0=\sum_{k=0}^{n-1}a_k$. 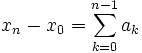Von der Reihe zeigen wir, dass sie eine geometrische Reihe als Majorante hat. Wegen der Vollständigkeit des Raumes folgt daraus die Konvergenz der Reihe, der Punkt 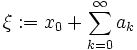$\xi:=x_0+\sum_{k=0}^\infty a_k$ ist der gesuchte Fixpunkt.

Beweis im metrischen Raum

Wir betrachten das Problem im vollständigen metrischen Raum. Wieder konstruieren wir die rekursive Folge. Statt direkt mit Teleskopsummen zu operieren, betrachten wir die Abstände 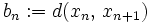$b_n:=d(x_n,\,x_{n+1})$. Die mehrfache Anwendung der Dreiecksungleichung auf die Differenz beliebiger Folgenglieder liefert

$d(x_n,\,x_{n+p})\le\sum_{k=n}^{n+p-1}b_k$.

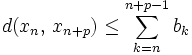Zeigen wir also, dass die Reihe 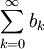$\sum_{k=0}^\infty b_k$ konvergiert, genauer eine geometrische Reihe als Majorante hat, so ist 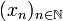$(x_n)_{n\in\mathbb N}$ eine Cauchy-Folge und damit konvergent. Nach Voraussetzung der Kontraktivität gilt:

$b_{n+1}=d(x_{n+1},\,x_{n+2})=d\left(\varphi(x_n),\,\varphi(x_{n+1})\,\right)\le\lambda d(x_n,x_{n+1})=\lambda b_n$.

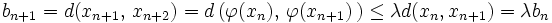Also ist 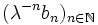$(\lambda^{-n}b_n)_{n\in\mathbb N}$ eine monoton fallende Folge, mithin 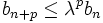$b_{n+p}\le\lambda^pb_n$, insbesondere

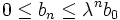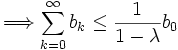$0\le b_n\le\lambda^n b_0$, $\Longrightarrow \sum_{k=0}^\infty b_k\le \frac1{1-\lambda}b_0$ wegen λ<1.

Es gibt also den Grenzwert 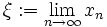$\xi:=\lim_{n\to\infty}x_n$. Für die Abschätzungen erhalten wir

$d(x_n,\xi)\le\sum_{k=n}^\infty b_k\le\frac1{1-\lambda} b_n\le \frac{\lambda^n}{1-\lambda}b_0$

Insbesondere ist 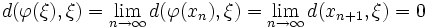$d(\varphi(\xi),\xi)=\lim_{n\to\infty}d(\varphi(x_n),\xi)=\lim_{n\to\infty}d(x_{n+1},\xi)=0$, also 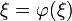$\xi = \varphi(\xi)$ tatsächlich ein Fixpunkt. Für einen weiteren möglichen Fixpunkt η gilt 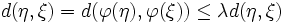$d(\eta,\xi)=d(\varphi(\eta),\varphi(\xi))\le\lambda d(\eta,\xi)$, was nur bei η = ξ möglich ist

Anwendungen

Dieser Satz wird in vielen konstruktiven Sätzen der Analysis benutzt, die wichtigsten sind:

• das inverse- und implizite-Funktionen-Theorem
• der Existenz- und Eindeutigkeitssatz von Picard-Lindelöf für gewöhnliche Differentialgleichungen