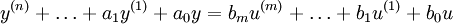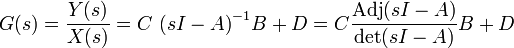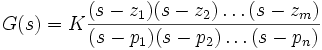Transferfunktion

Die Übertragungsfunktion ist eine mathematische Beschreibung für das Verhalten eines linearen, zeitinvarianten Systems. Man erhält die Übertragungsfunktion durch Laplace-Transformation der Differenzialgleichung, die das System beschreibt. Aus ihr lassen sich Systemeigenschaften wesentlich einfacher erhalten, als durch Lösung der Differenzialgleichung (was oft nicht mehr analytisch möglich ist).

Allgemeine Beschreibung

Zeitkontinuierliche lineare Systeme werden durch die lineare Differentialgleichung n-ter Ordnung

$y^{(n)} + \ldots + a_{1}y^{(1)} + a_{0}y = b_{m}u^{(m)} + \ldots + b_{1}u^{(1)} + b_{0}u$

beschrieben. Falls die Koeffizienten a_i und b_k alle konstant sind ist die Laplace-Transformation ausführbar. Mit den Anfangsbedingungen

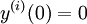$y^{(i)}(0)=0\;$ für alle 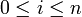$0\leq i \leq n\;$ lautet die Laplace-Transformierte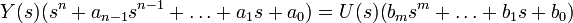

$Y(s)(s^{n} + a_{n-1}s^{n-1} + \ldots + a_{1}s + a_{0})=U(s)(b_{m}s^{m} + \ldots + b_{1}s + b_{0})$

und die Übertragungsfunktion

$G(s) =\frac{Y(s)}{U(s)} = \frac{b_{m}s^{m} + \ldots + b_{1}s + b_{0}}{s^{n} + a_{n-1}s^{n-1} + \ldots + a_{1}s + a_{0}}$.

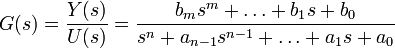Dieses zeitkontinuierliche Modell beschreibt das Verhalten des Systems vollständig, wenn alle Oberwellen erfasst sind, das heißt, die Ordnung n ist groß.

In gleicher Weise können Übertragungsfunktionen (z-Übertragungsfunktionen) auch für lineare, zeitinvariante Abtastsysteme modelliert werden. Statt der Laplacetransformation wird dann die z-Transformation verwendet. Dieses zeitdiskrete Modell erlaubt es, auch für Wertefolgen, wie sie bei Abtastsystemen am Ein- und Ausgang auftreten, Übertragungsfunktionen zu bestimmen.

Übertragungsfunktion eines Systems in der Zustandsraumdarstellung

Wird ein System in der Zustandsraumdarstellung beschrieben, so erhält man die Übertragungsfunktion durch:

$G(s) = \frac{Y(s)}{X(s)} = C\ {(sI - A)}^{-1} B + D= C{\frac{\mathrm{Adj} (sI-A)}{\mathrm{det}(sI-A)}} B + D \,$

Pol-Nullstellendarstellung

Die Übertragungsfunktion in Pol-Nullstellen-Darstellung ist:

$G(s) = K\frac{{(s - z_1 )(s - z_2 ) \ldots (s - z_m )}}{{(s - p_1 )(s - p_2 ) \ldots (s - p_n )}}$

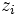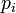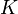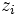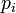Die $z_i\;$ sind Nullstellen und die $p_i\;$ Pole der Übertragungsfunktion. Durch eine Angabe des Verstärkungsfaktors $K\;$, $z_i\;$ und $p_i\;$ ist die Übertragungsfunktion vollständig bestimmt. Diese Darstellung ist z. B. für Stabilitätsuntersuchungen wichtig.

Experimentelle Ermittlung

Die Übertragungsfunktion ist im Gegensatz zum Frequenzgang nicht direkt messbar, kann aber mit Methoden der Systemidentifikation unter anderem aus der Sprungantwort bestimmt werden.

Zusammenhang mit dem Frequenzgang

Wird der komplexe Parameter 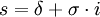$s=\delta + \sigma\cdot i\;$ durch die imaginäre Kreisfrequenz 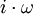$i \cdot \omega\;$ ersetzt, geht die Übertragungsfunktion formal in den Frequenzgang 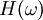$H(\omega)\;$ über.

$G(i\cdot \omega)=H(\omega)$.

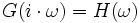Siehe auch

• Frequenzgang
• Fourier-Transformation
• Laplace-Transformation
• Signalanalyse

Literatur

• Heinz Unbehauen: Regelungstechnik. Klassische Verfahren zur Analyse und Synthese linearer kontinuierlicher Regelsysteme. 9. Auflage. Bd. 1, Vieweg & Sohn Verlagsgesellschaft, Braunschweig 1997, ISBN 978-3-5288-3332-9.