Laplace-Filter

Der Laplace-Filter bzw. diskrete Laplace-Operator ist ein Filter zur Kantendetektion, der den Laplace-Operator (Summe der beiden reinen zweiten Ableitungen) approximiert:

$\Delta f= \frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2}$

Unter einer Kante versteht man nun eine Kurve, entlang derer der Gradient des Bildes immer in Normalenrichtung zeigt. Das Vektorfeld $\nabla f$ ist also im Bereich der Kante quellenfrei. Eine Kante kann sich also nur einstellen, falls folgende Gleichung erfüllt ist:

$0=\nabla\cdot(\nabla f)=\Delta f$

Man sucht also die Nulldurchgänge eines Laplace-gefilterten Bildes. Allerdings ist hierbei zu beachten, dass auch Δf homogener Flächen gleich null sind. Der Laplace-Filter liefert also nur eine Obermenge der möglichen Kanten.

Funktionsweise

Berechnung der zweiten Ableitung von Kanten in einem verrauschten 1D-Signal

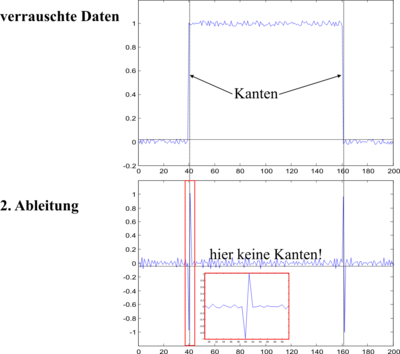
In der nebenstehenden Abbildung ist ein verrauschtes Signal gezeigt, von dem die zweite Ableitung berechnet wurde. Die Kante taucht hier als Nulldurchgang des Signals auf. Auf ein diskretes Signal g_n bzw. g_nm wird der Laplace-Operator über eine Faltung angewendet. Dabei kann man folgende einfache Faltungsmasken verwenden:

1D: $\vec{D}^2_x=\begin{bmatrix}1 & -2 & 1\end{bmatrix}$

2D: $\mathbf{D}^2_{xy}=\begin{bmatrix}0 & 1 & 0\\1 & -4 & 1\\0 & 1 & 0\end{bmatrix}$

Für das 2D-Filter gibt es noch eine zweite Variante, welche im Unterschied zur oberen Variante zusätzlich auf 45°-Kanten anspricht:

2D: $\mathbf{D}^2_{xy}=\begin{bmatrix}1 & 1 & 1\\1 & -8 & 1\\1 & 1 & 1\end{bmatrix}$

Diese Faltungsmasken erhält man durch die Diskretisierung der Differenzenquotienten. Am Ende des Artikels sieht man Beispiele für die Anwendung des Laplace-Filters.

Transferfunktion und Isotropie des Filters

Transferfunktion verschiedener Laplace-Filter

Die Transferfunktion (Fourier-Transformierte) des idealen Laplace-Operators Δ lautet:

$\Delta=\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\ \ \ \ \circ-\bullet\ \ \ \ -4\pi^2|\vec k|^2$

Ein diskretisierter Laplace-Operator muss diese parabolische Transferfunktion möglichst gut approximieren.

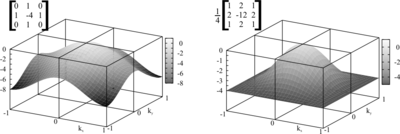
Die Abbildung rechts zeigt die Transferfunktion des ersten 2D-Laplace-Filters. Man sieht deutlich die Anisotropie und den Hochpass-Charakter der Transferfunktion. Als Formel lautet sie:

$\hat{l}(\vec k)=-4\sin^2(\pi k_x/2)-4\sin^2(\pi k_y/2)$

Sie zeigt um $\vec k=0$ Ähnlichkeit zur idealen Transferfunktion des Laplace-Operators.

Man kommt zu einer isotroperen Approximation des Laplace-Operator, wenn man eine etwas andere Darstellung des Laplace-Filters wählt:

$4(\mathcal{B}^2-\mathcal{I}) = \frac{1}{4} \begin{bmatrix} 1 & 2 & 1 \\ 2 & -12 & 2 \\ 1 & 2 & 1 \end{bmatrix}$

Dabei ist $\mathcal{B}^2$ der 3×3-Binomialfilter (Glättungsfilter) und $\mathcal{I}$ ein "Einheits-Filter"/δ-Puls, der das Bild auf sich selbst abbildet (Die Punktantwort ist überall null, bis auf das zentrale Pixel. Dort ist sie 1). Die Transferfunktion dieses Filters lautet:

$\hat{l}(\vec k)=-4\cos^2(\pi k_x/2)\cdot\cos^2(\pi k_y/2)-4$

Diese Transferfunktion ist ebenfalls in der Abbildung rechts enthalten. Es zeigt sich, dass sie wesentlich isotroper ist als die erste Version.

Beispielbilder

• 

  Originalbild

• 

  Bild gefiltert mit der einfachsten Filtermaske (Anklicken zum Vergrößern)

• 

  Bild gefiltert mit der zweiten Filtermaske (Anklicken zum Vergrößern)

Siehe auch

• Prewitt-Operator
• Sobel-Operator

Literatur

• Bernd Jähne: Digitale Bildverarbeitung. 6., überarbeitete und erweiterte Auflage. Springer-Verlag, Berlin 2005, ISBN 3-540-24999-0