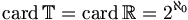Transzendente Zahlen

Eine reelle Zahl (oder allgemeiner: eine komplexe Zahl) x heißt transzendent, wenn sie nicht als Lösung einer algebraischen Gleichung beliebigen (endlichen) Grades

$a_{n}x^{n} + \dots + a_{2}x^2 + a_{1}x + a_{0} = 0$

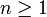für $n \geq 1$ mit ganzzahligen oder allgemein rationalen Koeffizienten a_k auftreten kann, wobei 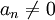$a_{n} \neq 0$ gelten soll. Andernfalls handelt es sich um eine algebraische Zahl. Jede transzendente Zahl ist überdies irrational.

Grad einer algebraischen Zahl

Im Weiteren wird es außerdem wichtig sein, eine Definition des sogenannten Grades einer algebraischen Zahl zu besitzen. Eine komplexe Zahl x wird als algebraische Zahl vom Grad n bezeichnet, wenn sie der algebraischen Gleichung

$f(x) = a_{n}x^{n} + \dots + a_{1}x + a_{0} = 0 \, (n \ge 1, \, a_n \ne 0, \, a_k \in \mathbb{Z})\, ,$

aber keiner derartigen Gleichung geringeren Grades genügt.

Geschichtliche Entwicklung des Transzendenzbegriffs

Die Vorstellung der mathematischen Transzendenz kam im Laufe des 18. Jahrhunderts ganz allmählich in den Überlegungen großer Mathematiker wie Gottfried Wilhelm Leibniz (omnem rationem transcendunt) und Leonhard Euler auf, die zwar keine strenge Definition dieses Begriffs besaßen, sich aber trotzdem sicher waren, dass es solche mathematisch „schwer fassbaren“ Zahlen geben müsse, von denen Euler schrieb, sie „überschreiten […] die Wirksamkeit algebraischer Methoden“. 1748 behauptete Euler in seinem Lehrbuch Introductio in Analysin Infinitorum sogar, dass bei positivem rationalem 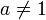$a \neq 1$ und natürlichem b, das keine Quadratzahl ist, die Zahl 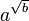$a^{\sqrt{b}}$ nicht rational ist, aber auch „nicht mehr irrational“ sei (wobei er unter „irrationale Zahlen“ den heute algebraische Zahlen genannten Zahlenbereich verstand). Tatsächlich wurde diese Transzendenzvermutung 1934 als Spezialfall eines Resultats des russischen Mathematikers Alexander Ossipowitsch Gelfond sowie des deutschen Mathematikers Theodor Schneider in ihrer Richtigkeit bestätigt. Ihre Beweise unterscheiden sich in wesentlichen Punkten.

Joseph Liouville konnte 1844 als Erster die Existenz transzendenter Zahlen beweisen und war imstande, mittels seiner konstruktiven Beweismethode explizite Beispiele zu liefern. In seiner Arbeit konnte er zeigen, dass es für jede algebraische Zahl x vom Grad 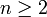$n\ge 2$ eine Konstante c gibt, so dass für jede rationale Approximation p / q:

$\left|x-\frac{p}{q}\right|>\frac{c}{q^n}$

gilt. Daraus folgt, dass die Liouville-Zahl

$L = \sum_{k=1}^{\infty} 10^{-k!} = 0{,}110001000000000000000001000\dots$

transzendent ist.

Siehe Beweis des Approximationssatz von Liouville im Beweisarchiv

Im Jahr 1874 konnte Georg Cantor nicht nur abermals die Existenz von transzendenten Zahlen beweisen, sondern sogar zeigen, dass es „mehr“ transzendente als algebraische Zahlen gibt. Im Gegensatz zu Liouville verwendete Cantors Existenzbeweis für transzendente Zahlen keine zahlentheoretischen Eigenschaften der algebraischen Zahlen, sondern ist (aus heutiger Sicht) rein mengentheoretischer Natur. Die mathematisch exakte Formulierung des Begriffs „mehr“ war aber sicherlich das wichtigste Ergebnis von Cantors Arbeit, weil es das Wissen über das reelle Zahlensystem revolutionär vertiefte. Allerdings konnten sich seine neuartigen Ideen gegen einflussreiche konservative Kritiker wie Leopold Kronecker lange Zeit nicht durchsetzen. Er bewies, dass die Menge der algebraischen reellen Zahlen (in moderner Sprechweise) abzählbar ist, während die Menge aller reellen Zahlen überabzählbar (unendlich, aber nicht abzählbar) ist. Daraus folgt auch leicht, dass die Menge aller transzendenten Zahlen gleichmächtig mit der Menge aller reellen Zahlen (insbesondere: ebenfalls überabzählbar) ist.

Dieser Sachverhalt lässt sich mengensprachlich folgendermaßen ausdrücken:

Wenn 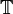$\mathbb{T}$ die Menge der transzendenten Zahlen und $\mathbb{R}$ die Menge der reellen Zahlen bezeichnet, dann gilt:

$\hbox{card} \, \mathbb{T} = \hbox{card} \, \mathbb{R} = 2^{\aleph_0}$

Hierbei ist 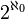$2^{\aleph_0}$ das mengentheoretische Symbol für die Mächtigkeit von 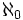$\mathbb{R}$; ${\aleph_0}$ (sprich „Aleph null“) ist das mengentheoretische Symbol für die Mächtigkeit einer abzählbar unendlichen Menge, insbesondere von $\mathbb{N}$.

Transzendenzbeweise von e und π

Die ursprünglichen Beweise der Transzendenz von e und π stammen von Charles Hermite bzw. von Ferdinand von Lindemann. Die Beweise sind allerdings nur sehr schwer nachzuvollziehen. Im Laufe der Zeit gab es aber immer wieder Vereinfachungen dieser Beweise. Einen sehr „eleganten“ Beweis veröffentlichte der berühmte Mathematiker David Hilbert (1862-1943) im Jahre 1893 in seinem Aufsatz „Über die Transzendenz der Zahlen e und π“.

Siehe Beweis der Transzendenz von e und π im Beweisarchiv

Beispiele für transzendente Zahlen

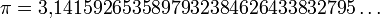• $\pi = 3{,}1415926535897932384626433832795\ldots$ Die Transzendenz von π, die von Carl Louis Ferdinand von Lindemann bewiesen wurde, ist auch der Grund für die Unlösbarkeit der Quadratur des Kreises mittels Zirkel und Lineal.
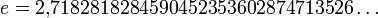• $e = 2{,}7182818284590452353602874713526\ldots$, die Eulersche Zahl, deren Transzendenz 1873 von Charles Hermite bewiesen werden konnte.
• e^a für algebraisches $a \ne 0$. Siehe auch Satz von Lindemann-Weierstraß.
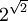• $2^{\sqrt{2}}$. Allgemeiner konnten Gelfond 1934 sowie Schneider 1934 unabhängig voneinander mit verschiedenen Methoden zeigen: Ist 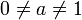$0 \ne a \ne 1$, a algebraisch, b algebraisch und irrational, dann ist a^b eine transzendente Zahl. Dies ist eine Teillösung von Hilberts siebtem Problem. Für transzendente b gilt dieser Satz offensichtlich nicht, da z.B. 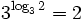$3^{\log_32} = 2$ (siehe auch Satz von Gelfond-Schneider).
• Der Sinus von 1
• ln(a) für rationales positives $a\ne 1$.
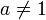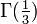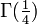• $\Gamma(\tfrac13)$ und $\Gamma(\tfrac14)$ (siehe Gammafunktion)
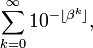• $\sum_{k=0}^{\infty}10^{-\lfloor\beta^{k}\rfloor},$ β > 1. Die Klammer 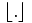$\lfloor . \rfloor$ ist hierbei die Gaußklammer.

Verallgemeinerung

Im Kontext allgemeiner Körpererweiterungen L/K betrachtet man ebenfalls Elemente in L, die algebraisch oder transzendent über K sind. Siehe dazu Algebraisches Element.

Literatur

• P. Bundschuh Zahlentheorie. Heidelberg, Springer 1998, 4. Aufl., ISBN 3-540-43579-4.
  Bietet einen einführenden Überblick zum Thema „transzendente Zahlen“ an.
• A. Baker Transcendental number theory. Cambridge, Cambridge University Press 1990 (Nachdruck), ISBN 052139791X.
  Ein anspruchsvolles Standardwerk, das tiefgreifende Theoreme entwickelt, aber profundes Vorwissen voraussetzt.
• A. Shidlovskii Transcendental numbers. Berlin, de Gruyter 1989, ISBN 3-11-011568-9.
  Besser lesbar als das Buch von Baker, dennoch ähnlich fundiert.
• A. Jones, S. Morris, K. Pearson Abstract Algebra and Famous Impossibilities. New York, Springer 1994, 2. Aufl., ISBN 0-387-97661-2.
  Enthält eine ausführliche Schritt-für-Schritt-Erläuterung des Lindemannschen Transzendenzbeweises für π.
• D. Hilbert Über die Transcendenz der Zahlen e und π. Mathematische Annalen 43, 216-219 (1893).
• Oskar Perron, Irrationalzahlen,1921.
• Th. Schneider Einführung in die transzendenten Zahlen. Springer-Verlag, Berlin-Göttingen-Heidelberg, 1957.

Siehe auch

• Liste besonderer Zahlen

Weblinks

• Proof that e is transcendental
• Der Beweis von Hermite-Lindemann, dass π und e transzendent sind (PDF)
• Der Beweis (nach Hilbert) von Fritsch, dass e transzendent ist (als PDF)
• Der Beweis (nach Hilbert) von Fritsch, dass π transzendent ist (als PDF)