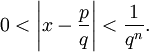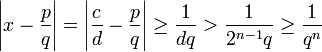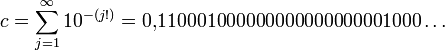Liouvillesche Zahlen

Als Liouvillesche Zahl bezeichnet man in der Zahlentheorie eine reelle Zahl x, welche die Bedingung erfüllt, dass für alle positiven ganzen Zahlen n ganze Zahlen p und q(q > 1) existieren, so dass

$0 < \left|x- \frac{p}{q}\right| < \frac{1}{q^n}.$

Alle Liouvillsche Zahlen sind irrational: Angenommen, es wäre anders, dann gäbe es ganze Zahlen c und d mit 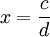$x = \frac{c}{d}$. Sei n eine positive ganze Zahl, sodass 2^{n − 1} > d. Wenn dann p und q ganze Zahlen sind, sodass q > 1 und 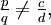$\tfrac pq \ne \tfrac cd,$ so ist

$\left|x- \frac{p}{q} \right|= \left| \frac{c}{d} - \frac{p}{q} \right| \ge \frac{1}{dq} > \frac{1}{2^{n-1}q} \ge \frac{1}{q^n}$

ein Widerspruch.

1844 zeigte Joseph Liouville, dass Zahlen mit dieser Eigenschaft nicht nur irrational sind, sondern auch immer transzendent. Damit gab er erstmals eine transzendente Zahl an, die Liouvillesche Konstante:

$c = \sum_{j=1}^\infty 10^{-(j!)} = 0{,}110001000000000000000001000\ldots$

Alle Liouvilleschen Zahlen sind transzendent, allerdings sind nicht alle transzendenten Zahlen liouvillesch.

Siehe auch

• Kettenbruch