Transzendentes Element

Die Begriffe algebraisches und transzendentes Element treten in der abstrakten Algebra auf und verallgemeinern das Konzept von algebraischen und transzendenten Zahlen.

Ist L/K eine Körpererweiterung, dann heißt ein Element a von L algebraisch über K, wenn es ein vom Nullpolynom verschiedenes Polynom mit Koeffizienten in K gibt, das a als Nullstelle hat. Ein Element, für das kein solches Polynom existiert, heißt transzendent über K.

Für die Erweiterung 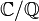$\Bbb C / \Bbb Q$ stimmen diese Begriffe mit denen der algebraischen bzw. transzendenten Zahl überein.

Beispiele

• Die Quadratwurzel von 2 ist algebraisch über $\Bbb Q$, denn sie ist eine Nullstelle des Polynoms X² − 2, dessen Koeffizienten rational sind.
• Die Kreiszahl π und die Eulersche Zahl e sind transzendent über $\Bbb Q$, aber algebraisch über $\Bbb R$, denn sie sind als reelle Zahlen definiert. Allgemeiner gilt:
• Jedes Element a des Körpers K ist algebraisch über K, denn es ist Nullstelle des linearen Polynoms X − a.
• Jede komplexe Zahl, die sich durch rationale Zahlen, die Grundrechenarten +,-,*,/ und Wurzelziehen (mit natürlichen Wurzelexponenten) bilden lässt, ist algebraisch über $\Bbb Q$.
• Aus der Galoistheorie folgt aber andererseits, dass es über $\Bbb Q$ algebraische Zahlen gibt, die sich nicht auf diese Weise darstellen lassen; vergleiche hierzu den Satz von Abel-Ruffini.
• Über dem Körper $\Bbb Q_p$ der p-adischen Zahlen ist e (als Grenzwert der Reihe der reziproken Fakultäten) algebraisch, denn für p>2 ist e^p und für p=2 ist e⁴ in $\Bbb Q_p$ enthalten.
• Bildet man zu einem beliebigen Körper K den Körper der Formalen Laurentreihen K((X)), so ist die formale Variable X ein transzendentes Element dieser Erweiterung.

Eigenschaften

Die folgenden Bedingungen sind äquivalent für ein Element a aus L (einem Oberkörper von K):

• a ist algebraisch über K
• die Körpererweiterung K(a)/K hat endlichen Grad, d.h. K(a) ist als K-Vektorraum endlichdimensional.
• K[a] = K(a).

Dabei ist K[a] die Ringadjunktion von a an K, die aus allen Elemente von L besteht, die sich als g(a) mit einem Polynom g über K schreiben lassen; K(a) ist dessen Quotientenkörper in L und besteht aus allen Elementen von L, die sich als g(a)/h(a) mit Polynomen g und h über K (h(a) ungleich 0) schreiben lassen.

Diese Charakterisierung kann genutzt werden, um zu zeigen, dass Summe, Differenz, Produkt und Quotient von über K algebraischen Elementen wieder algebraisch über K sind. Die Menge aller über K algebraischen Elemente von L bildet einen Zwischenkörper der Erweiterung L/K, den so genannten algebraischen Abschluss in L.

Minimalpolynom

Ist a algebraisch über K, dann gibt es viele Polynome $g\in K[X]$ mit g(a) = 0. Es gibt aber genau ein normiertes Polynom von kleinstem Grad mit Nullstelle a, dieses heißt das Minimalpolynom von a über K. Aus ihm kann man viele Eigenschaften von a ablesen. Zum Beispiel ist der Grad dieses Polynoms gleich dem Erweiterungsgrad von K(a) / K.