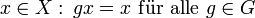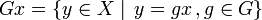Trennende Invariante

In der Mathematik versteht man unter einer Invariante eine zu einem Objekt assoziierte Größe, die sich bei einer jeweils passenden Klasse von Modifikationen des Objektes nicht ändert. Invarianten sind ein wichtiges Hilfsmittel bei Klassifikationsproblemen: Objekte mit unterschiedlichen Invarianten sind wesentlich verschieden; gilt auch die Umkehrung, d.h. sind Objekte mit gleichen Invarianten im wesentlichen identisch, so spricht man von einem vollständigen Satz von Invarianten oder von trennenden Invarianten.

Einführendes Beispiel

Die betrachteten Objekte sind Paare (x,y) reeller Zahlen, erlaubte Modifikationen bestehen darin, zu beiden Zahlen dieselbe beliebig gewählte Zahl zu addieren:

$(x,y)\quad\Longrightarrow\quad(x',y')=(x+z,y+z)$.

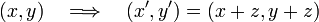Eine Invariante ist in diesem Fall die Differenz x − y der beiden Zahlen:

x' − y' = (x + z) − (y + z) = x − y.

Eine Interpretation dieses Beispiels könnte sein: x und y sind die Anfangs- und Endpunkt einer Stange, gemessen von einem festen Punkt in der Verlängerung der Stange. Die Modifikationen entsprechen einer Verschiebung der Stange um z, die Invariante ist die Länge der Stange.

In diesem Beispiel genügt bereits diese eine Invariante für eine vollständige Klassifikation: Zwei Zahlenpaare (x₁,y₁) und (x₂,y₂) gehen genau dann auseinander hervor, das heißt, es gibt ein z, so dass

x₁ + z = x₂ und y₁ + z = y₂,

wenn die Längen übereinstimmen:

x₁ − y₁ = x₂ − y₂.

(Beweis: Setze z = x₂ − x₁, dann ist y₁ + z = x₂ − (x₁ − y₁) = x₂ − (x₂ − y₂) = y₂.)

Weitere Beispiele

• Die Dimension eines Vektorraumes ist eine Isomorphie-Invariante, d.h., sind V und W isomorphe Vektorräume, so stimmen ihre Dimensionen überein. Bei endlichdimensionalen Vektorräumen gilt auch die Umkehrung: Zwei Vektorräume der gleichen Dimension sind isomorph.
• Die Determinante einer Matrix ist eine Ähnlichkeitsinvariante, d.h., sind A und B zwei Matrizen, für die es eine invertierbare Matrix S gibt, so dass B = SAS ^{− 1} gilt, so haben A und B dieselbe Determinante. Hier gilt die Umkehrung nicht, beispielsweise hat jede Drehung Determinante 1.
• Betti-Zahlen und Euler-Charakteristik sind topologische Invarianten, d.h. invariant unter Homöomorphismen.

Invarianten unter Operationen

Bei Gruppenoperationen spricht man ebenfalls von Invarianten: Ist X eine Punktmenge mit einer Operation der Gruppe G, so heißen die Punkte, die invariant bleiben,

$x\in X :\, gx=x\ \mathrm{f\ddot ur\ alle}\ g\in G$

Fixpunkte oder die G-invarianten Punkte.

Allgemeiner ist jede Bahn durch einen Punkt 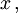$x\,,$ die durch die Gruppenoperation entsteht,

$Gx=\{y\in X \mid\, y=gx\,, g\in G\}$

invariant unter der Gruppenoperation.

Weiterführende Themen

In der theoretischen Physik besagt das Noether-Theorem den Zusammenhang von Symmetrien der Wirkung und Invarianten der Zeitentwicklung, die man in der Physik Erhaltungsgrößen nennt.