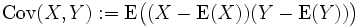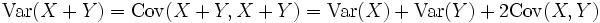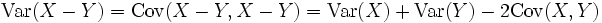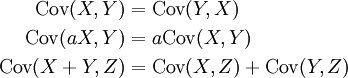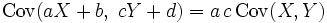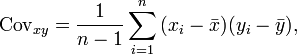- Unkorreliertheit
-
Die Kovarianz ist in der Statistik eine (nichtstandardisierte) Maßzahl für den Zusammenhang zweier statistischer Merkmale (im Folgenden X und Y).
- Die Kovarianz ist positiv, wenn X und Y tendenziell einen gleichsinnigen linearen Zusammenhang besitzen, d. h. hohe Werte von X gehen mit hohen Werten von Y einher und niedrige mit niedrigen.
- Die Kovarianz ist hingegen negativ, wenn X und Y einen gegensinnigen linearen Zusammenhang aufweisen, d. h. hohe Werte der einen Zufallsvariablen gehen mit niedrigen Werten der anderen Zufallsvariablen einher.
- Ist das Ergebnis 0, so besteht kein Zusammenhang oder ein nicht linearer Zusammenhang z. B. eine U-förmige Beziehung zwischen den beiden Variablen X und Y.
Die Kovarianz gibt zwar die Richtung einer Beziehung zwischen zwei Variablen an, über die Stärke des Zusammenhangs wird aber keine Aussage getroffen. Dies liegt an der Abhängigkeit des Ergebnisses von den Maßeinheiten der beteiligten Variablen X und Y. Ist z. B. die Kovarianz zweier Variablen mit der Maßeinheit "Meter" 5,2 so ist die Kovarianz der gleichen Werte in der Maßeinheit "Zentimeter" 520. Die Kovarianz ist deshalb in ihrer "Rohform" als Maßzahl für den stochastischen Zusammenhang nur wenig anschaulich und auch schwer vergleichbar.
Um einen Zusammenhang vergleichbar zu machen, muss die Kovarianz normiert werden. Man erhält dann den Korrelationskoeffizienten, dessen Maßzahl sich im Intervall von -1 bis +1 bewegt ( +1: perfekter linearer Zusammenhang, 0: gar kein linearer Zusammenhang, -1: perfekter gegensätzlicher linearer Zusammenhang).
Inhaltsverzeichnis
Definition
Sind X und Y zwei Zufallsvariablen, die quadratisch integrierbar sind, d. h. die Erwartungswerte
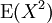 und
und 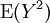 existieren, dann heißt
existieren, dann heißtdie Kovarianz von X und Y.
Eigenschaften
Beziehung zur Varianz
Die Kovarianz ist eine Verallgemeinerung der Varianz, denn es gilt
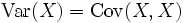 .
.
Weiterhin gilt
Beziehung zum Korrelationskoeffizienten
Wird die Kovarianz auf das Produkt der Standardabweichungen von X und Y bezogen (also standardisiert), so spricht man vom Korrelationskoeffizienten
![\operatorname{Kor}(X,Y) := \varrho(X,Y) := \frac{\operatorname{Cov}(X,Y)}{\sqrt{\operatorname{Var}(X)} \cdot \sqrt{\operatorname{Var}(Y)}}= \frac{\operatorname{E}\left[(X-\operatorname{E}(X))(Y-\operatorname{E}(Y))\right]}{\sqrt{\operatorname{Var}(X)} \cdot \sqrt{\operatorname{Var}(Y)}}](/pictures/dewiki/99/c4d4c8c5f575e2490f2df5e1cb8e102f.png) .
.
Verschiebungssatz
Der Verschiebungssatz von Steiner liefert eine alternative Darstellung der Kovarianz
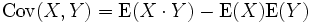 .
.
Symmetrie und Linearität
Die Kovarianz ist eine symmetrische Bilinearform auf dem Vektorraum der quadratisch integrierbaren Zufallsvariablen, d. h. es gilt:
Wegen der Symmetrie ist die Kovarianz auch im zweiten Argument linear.
Lineare Transformation
Ist c eine konstante Zufallsvariable, dann ist
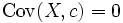 . Als Folgerung erhält man die lineare Transformation:
. Als Folgerung erhält man die lineare Transformation:Diese Eigenschaft bedeutet, dass die Kovarianz vom Maßstab der Zufallsvariablen abhängt. So erhält man beispielsweise die zehnfache Kovarianz, wenn man anstatt X die Zufallsvariable 10X betrachtet. Da diese Eigenschaft die absoluten Werte der Kovarianz schwer interpretierbar macht, betrachtet man häufig stattdessen den maßstabsunabhängigen Korrelationskoeffizienten.
Unkorreliertheit
Falls
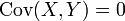 , so heißen die Zufallsvariablen X und Y unkorreliert.
, so heißen die Zufallsvariablen X und Y unkorreliert.Wenn die Zufallsvariablen
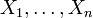 paarweise unkorreliert sind (d. h.
paarweise unkorreliert sind (d. h. 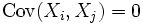 für
für 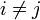 ), dann gilt für die Varianz der Summe der Zufallsvariablen
), dann gilt für die Varianz der Summe der Zufallsvariablen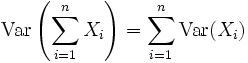 .
.
Unkorreliertheit bedeutet nicht zwingend, dass die Zufallsvariablen stochastisch unabhängig sind, denn es können nichtlineare Abhängigkeitsstrukturen vorliegen, die die Kovarianz nicht erfassen kann. Dagegen gilt für zwei stochastisch unabhängige Zufallsvariablen
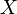 und
und 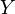 immer
immer 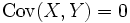 .
.Kovarianzschätzung für zwei Merkmale einer Stichprobe
Es werden für zwei Zufallsvariablen X und Y in einer Stichprobe je n Werte xi und yi
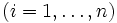 erhoben. Man schätzt die Kovarianz der Zufallsvariablen erwartungstreu mit der (korrigierten) Stichproben-Kovarianz
erhoben. Man schätzt die Kovarianz der Zufallsvariablen erwartungstreu mit der (korrigierten) Stichproben-Kovarianz(mit den Mittelwerten
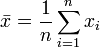 und
und 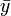 entsprechend.)
entsprechend.)Auch hier gilt analog zu oben der Verschiebungssatz
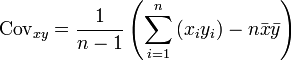 .
.
Der Verschiebungssatz wird vor allem angewendet, wenn die Kovarianz von Hand ermittelt wird. Wird die Stichproben-Kovarianz numerisch berechnet, sollte der Verschiebungssatz nicht gebraucht werden, weil das Multiplizieren der Datenwerte
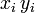 zu Rundungsfehlern führen kann. Dagegen sind die zentrierten Datenwerte
zu Rundungsfehlern führen kann. Dagegen sind die zentrierten Datenwerte 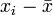 und
und 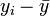 betragsmäßig deutlich kleiner.
betragsmäßig deutlich kleiner.Die restlichen Eigenschaften ergeben sich ebenfalls analog zu oben. Es existieren entsprechende Schätzer für die Kovarianzmatrix.
Siehe auch
Wikimedia Foundation.