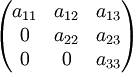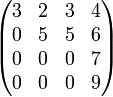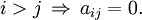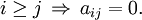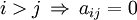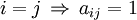Untere Dreiecksmatrix

Unter einer Dreiecksmatrix versteht man in der Mathematik eine quadratische Matrix, die sich dadurch auszeichnet, dass alle Einträge unterhalb (obere Dreiecksmatrix) bzw. oberhalb (untere Dreiecksmatrix) der Hauptdiagonale null sind. Sind zusätzlich die Einträge auf der Hauptdiagonale alle null, so spricht man von einer echten oder strikten Dreiecksmatrix.

Dreiecksmatrizen spielen unter anderem beim Lösen von Linearen Gleichungssystemen mittels der LU-Zerlegung eine wichtige Rolle, welche darauf basiert, eine Matrix in das Produkt einer oberen und einer unteren Dreiecksmatrix zu zerlegen.

Beispiele

$\begin{pmatrix} a_{11} & a_{12} & a_{13} \\ 0 & a_{22} & a_{23} \\ 0 & 0 & a_{33} \end{pmatrix}$

$\begin{pmatrix} 3 & 2 & 3 & 4 \\ 0 & 5 & 5 & 6 \\ 0 & 0 & 0 & 7 \\ 0 & 0 & 0 & 9 \end{pmatrix}$

Obere und untere Dreiecksmatrix

Eine Matrix wird obere Dreiecksmatrix genannt, falls alle Einträge unterhalb der Hauptdiagonalen 0 sind. Für die Einträge auf der Hauptdiagonale selbst gibt es keine Beschränkungen.

Für eine obere Dreiecksmatrix gilt somit:

$i > j \, \Rightarrow \, a_{ij} = 0.$

Analog heißt eine Matrix untere Dreiecksmatrix, falls alle Einträge oberhalb der Hauptdiagonalen 0 sind

Trigonalisierbarkeit

Hauptartikel: Trigonalisierung.

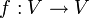Ist V ein Vektorraum über dem Körper $\mathbb{K}$ und hat man eine quadratische Matrix A, die die Darstellung einer linearen Abbildung $f: V \to V$ (Vektorraum-Endomorphismus) ist, so heißt diese trigonalisierbar, falls sie bei Betrachtung in einer anderen Basis, eine obere Dreiecksgestalt aufweist, also trigonal ist. Gesucht ist also eine trigonale Matrix B, die ähnlich zu A ist.

Dies ist der Fall, falls das charakteristische Polynom χ_A über dem Körper $\mathbb{K}$ in Linearfaktoren zerfällt.

Ist 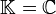$\mathbb{K} = \mathbb{C}$, so ist jede Matrix trigonalisierbar, da nach dem Fundamentalsatz der Algebra der Körper $\mathbb{C}$ algebraisch abgeschlossen ist.

Strikte obere und untere Dreiecksmatrix

Es gibt zwei verschiedene Definitionen für den Begriff strikte obere Dreiecksmatrix, je nachdem, ob man allgemeine oder nur invertierbare Matrizen betrachtet. Erstere sind nilpotent, letztere unipotent. Die folgenden Definitionen erfolgen analog für strikte untere Dreiecksmatrizen.

Nilpotente Dreiecksmatrizen

Bei einer strikten oberen Dreiecksmatrix in diesem Sinne sind alle Einträge sowohl unterhalb als auch auf der Hauptdiagonale der Matrix 0. Es gilt somit:

$i \geq j \, \Rightarrow \, a_{ij} = 0.$

Unipotente Dreiecksmatrizen

Bei einer strikten oberen Dreiecksmatrix im Sinne invertierbarer Matrizen sind alle Einträge unterhalb der Hauptdiagonale der Matrix 0, während die Diagonaleinträge alle gleich 1 sind. Es gilt somit:

$i > j \, \Rightarrow \, a_{ij} = 0$

$i = j \, \Rightarrow \, a_{ij} = 1$

Eine derartige Matrix A ist unipotent, d. h. die Matrix A − I ist nilpotent, es gibt also eine Zahl n, so dass gilt:

(A − I)ⁿ = 0.

Eigenschaften

Es lässt sich beweisen:

• Das Produkt von unteren (oberen) Dreiecksmatrizen ist wieder eine untere (obere) Dreiecksmatrix.
• Das Produkt von strikten unteren (oberen) Dreiecksmatrizen ist wieder eine strikte untere (obere) Dreiecksmatrix.
• Die Inverse einer invertierbaren unteren (oberen) Dreiecksmatrix ist eine untere (obere) Dreiecksmatrix.
• Die Determinante einer Dreiecksmatrix ist das Produkt ihrer Hauptdiagonalelemente.
• Die Eigenwerte einer Dreiecksmatrix sind die Elemente der Hauptdiagonalen.

Algebraische Eigenschaften

• Die Menge aller oberen Dreiecksmatrizen bildet eine auflösbare Liealgebra, die Menge aller nilpotenten oberen Dreiecksmatrizen eine nilpotente Liealgebra.
• Die Menge aller invertierbaren oberen Dreiecksmatrizen bildet eine auflösbare Gruppe, die Menge aller unipotenten oberen Dreiecksmatrizen eine nilpotente Gruppe.
• Die Anzahl der Elemente einer Dreiecksmatrix, die von Null verschieden sein können, ist 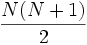$N(N+1)\over2$; dies ist auch die Dimension als Liegruppe oder algebraische Gruppe.

Literatur

• Gerd Fischer: Lineare Algebra, Vieweg-Verlag, ISBN 3-528-97217-3.