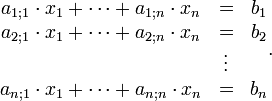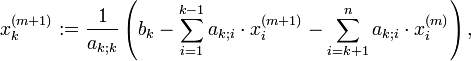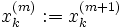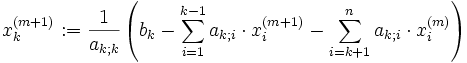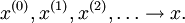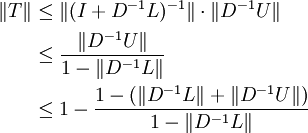Einzelschrittverfahren

In der numerischen Mathematik ist das Gauß-Seidel-Verfahren oder Einzelschrittverfahren, (nach Carl Friedrich Gauß und Ludwig Seidel) ein Algorithmus zur näherungsweisen Lösung von linearen Gleichungssystemen. Es ist, wie das Jacobi-Verfahren und das SOR-Verfahren, ein spezielles Splitting-Verfahren. Das Verfahren wurde zuerst von Gauß entwickelt, aber nicht veröffentlicht, später wurde es, bevor seine Anwendung durch Gauß bekannt war, von Seidel veröffentlicht.

Entwickelt wurde das Verfahren, da das Gaußsche Eliminationsverfahren, ein exakter Löser, für Rundungsfehler sehr anfällig ist. Eine iterative Vorgehensweise hat diesen Nachteil nicht.

Beschreibung des Verfahrens

Gegeben ist ein lineares Gleichungssystem in n Variablen mit den n Gleichungen

$\begin{matrix} a_{1;1}\cdot x_1+\dots+a_{1;n}\cdot x_n&=&b_1\\ a_{2;1}\cdot x_1+\dots+a_{2;n}\cdot x_n&=&b_2\\ &\vdots&\\ a_{n;1}\cdot x_1+\dots+a_{n;n}\cdot x_n&=&b_n\\ \end{matrix}.$

Um dieses zu lösen, wird die k-te Gleichung nach der k-ten Variablen x_k aufgelöst, d.h. für den (m + 1)-ten Iterationsschritt:

$x^{(m+1)}_k:=\frac1{a_{k;k}}\left(b_k-\sum_{i=1}^{k-1} a_{k;i}\cdot x^{(m+1)}_i -\sum_{i=k+1}^n a_{k;i}\cdot x^{(m)}_i\right),$

wobei die vorher berechneten Werte des aktuellen Iterationsschritts mit verwendet werden, im Gegensatz zum Jacobi-Verfahren. Diese Ersetzung wird, ausgehend von einer willkürlichen Startbelegung der Variablen, sukzessive wiederholt. Als minimale Bedingung lässt sich hier festhalten, dass die Diagonalelemente a_k;k von Null verschieden sein müssen.

Als Algorithmusskizze mit Abbruchbedingung ergibt sich:

wiederhole

fehler: = 0

für k = 1 bis n

$x^{(m)}_k:=x^{(m+1)}_k$

$x^{(m+1)}_k:=\frac1{a_{k;k}}\left(b_k-\sum_{i=1}^{k-1} a_{k;i}\cdot x^{(m+1)}_i -\sum_{i=k+1}^n a_{k;i}\cdot x^{(m)}_i\right)$

$\text{fehler}:=\max(\text{fehler}, |x^{(m+1)}_k-x^{(m)}_k|)$

nächstes k

m: = m + 1

bis fehler < fehlerschranke

Dabei wurde die Erstbelegung des Variablenvektors und eine Fehlerschranke als Eingangsgrößen des Algorithmus angenommen, die Näherungslösung ist die vektorielle Rückgabegröße. Die Fehlerschranke misst hier, welche Größe die letzte Änderung des Variablenvektors hatte.

Herleitung des Verfahrens

Beschreibung des Verfahrens in Matrixschreibweise

Die Matrix A des linearen Gleichungssystems 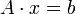$A \cdot x = b$ wird zur Vorbereitung in eine Diagonalmatrix D, eine strikte obere Dreiecksmatrix U und eine strikte untere Dreiecksmatrix L zerlegt, so dass gilt:

A = L + D + U.

In jedem Iterationsschritt gilt dann Dx^(neu) = b − Lx^(neu) − Ux^(alt). Nach Umstellen ergibt sich formal

(D + L)x^(neu) = b − Ux^(alt) und daraus x^(neu) = (D + L) ^{− 1}(b − Ux^(alt)).

Man legt dann einen Startvektor x⁽⁰⁾ fest und setzt ihn in die Iterationsvorschrift ein:

x^{(k + 1)} = − (D + L) ^{− 1}Ux^(k) + (D + L) ^{− 1}b.

Da es der erste Iterationsschritt ist, hat dabei k den Wert Null. Das Ergebnis der Rechnung ist ein erster Näherungswert x⁽¹⁾ für den gesuchten Lösungsvektor x. Diesen Näherungswert kann man seinerseits in die Iterationsvorschrift einsetzen und gewinnt einen besseren Näherungswert x⁽²⁾, den man wieder einsetzen kann. Wiederholt man diesen Vorgang, gewinnt man eine Folge von Werten, die sich dem Lösungsvektor immer mehr annähern, wenn die Konvergenzbedingungen (s. unten) erfüllt sind:

$x^{(0)}, x^{(1)}, x^{(2)}, \ldots \rightarrow x.$

Diagonaldominanz und Konvergenz

Die Konvergenzgeschwindigkeit des Verfahrens hängt vom Spektralradius der Iterationsmatrix T = (D + L) ^{− 1}U ab. Dieser sollte so klein wie möglich sein, muss aber immer kleiner als 1 sein. In diesem Falle ist der Fixpunktsatz von Banach bzw. der Konvergenzsatz der Neumann-Reihe (auf eine hinreichend große Potenz von T) anwendbar und das Verfahren konvergiert. Im gegenteiligen Fall divergiert das Verfahren, wenn die rechte Seite des Gleichungssystems ein Eigenvektor zu einem Eigenwert mit Betrag größer als 1 ist.

Die Bestimmung des Spektralradius ist für den praktischen Einsatz meist ungeeignet. Man gibt daher auch hinreichende Konvergenzbedingungen für „bequeme“ Matrixnormen an. Allgemein muss die Matrixnorm der Verfahrensmatrix T kleiner als 1 sein. Diese Matrixnorm ist gleichzeitig die Kontraktionskonstante im Sinne des banachschen Fixpunktsatzes.

Im Falle, dass sowohl D ^{− 1}U als auch D ^{− 1}L "kleine" Matrizen bzgl. der gewählten Matrixnorm sind, gibt es die folgende Abschätzung der Matrixnorm für 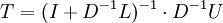$T=(I+D^{-1}L)^{-1}\cdot D^{-1}U$ (siehe Neumann-Reihe für den ersten Faktor):

$\begin{align} \|T\| &amp;amp;\le \|(I+D^{-1}L)^{-1}\|\cdot\|D^{-1}U\|\\ &amp;amp;\le \frac{\|D^{-1}U\|}{1-\|D^{-1}L\|}\\ &amp;amp;\le 1-\frac{1-\left(\|D^{-1}L\|+\|D^{-1}U\|\right)}{1-\|D^{-1}L\|} \end{align}$

Der letzte Ausdruck ist für 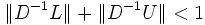$\|D^{-1}L\|+\|D^{-1}U\|&amp;lt;1$ ebenfalls kleiner als 1. Obwohl die Konvergenzbedingung diejenige des Jabobi-Verfahrens ist, ist die so erhaltene Abschätzung der Kontraktionskonstante 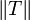$\|T\|$ des Gauß-Seidel-Verfahrens immer kleinergleich der entsprechenden Abschätzung der Kontraktionskonstante des Jabobi-Verfahrens.

Das einfachste und gebräuchlichste hinreichende Konvergenzkriterium der Diagonaldominanz ergibt sich für die Supremumsnorm 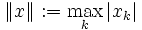$\|x\|:=\max_k|x_k|$ der Vektoren und deren induzierter Matrixnorm 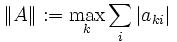$\|A\|:=\max_k\sum_i|a_{ki}|$. Es verlangt die Erfüllung des Zeilensummenkriteriums, also der Ungleichung

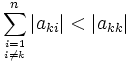$\sum_{i=1 \atop i\ne k}^n|a_{ki}|&amp;lt;|a_{kk}|$ für $k=1,\ldots,n$.

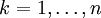Je größer die kleinste Differenz zwischen rechten und linken Seiten der Ungleichung ist, desto schneller konvergiert das Verfahren. Man kann versuchen, diese Differenz mittels Zeilen- und Spaltenvertauschungen zu vergrößern, d.h. durch Umnummerieren der Zeilen und Spalten. Dabei kann man beispielsweise anstreben, die betragsgrößten Elemente der Matrix auf die Diagonale zu bringen. Die Zeilenvertauschungen müssen natürlich auch auf der rechten Seite des Gleichungssystems vollzogen werden.

Anwendungen

Für moderne Anwendungen wie die Lösung großer dünnbesetzter Gleichungssysteme, die aus der Diskretisierung partieller Differentialgleichungen stammen, ist das Verfahren ungeeignet. Es wird jedoch mit Erfolg als Vorkonditionierer in Krylow-Unterraum-Verfahren oder als Glätter in Mehrgitterverfahren eingesetzt.

Literatur

• A. Meister: Numerik linearer Gleichungssysteme, 2. Auflage, Vieweg 2005, ISBN 3528131357
• R. Barrett et al.: Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, 2nd Edition, SIAM Philadelphia, 1994

Weblinks

• Eric W. Weisstein et al. "Gauss-Seidel Method." MathWorld