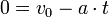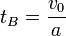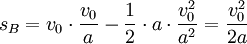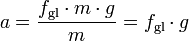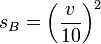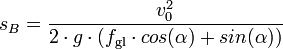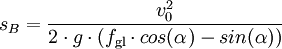- Vollbremsdauer
-
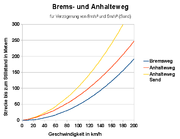
Der Bremsweg ist die Strecke, die ein Fahrzeug vom Beginn der Bremsung bis zum Ende der Bremsung zurücklegt. Entscheidend für die Länge des Bremsweges ist die gefahrene Geschwindigkeit und die Verzögerung. Der Anhalteweg ist länger und berücksichtigt die Reaktionszeit.
Inhaltsverzeichnis
Bremsung
Bei einer Bremse, die direkt auf den Fahrweg wirkt, etwa eine Magnetschienenbremse oder einer aerodynamischen Bremse, ist der Bremsweg von der Masse und der Geschwindigkeit abhängig. Dies gilt auch bei einer Bremse, die auf eine formschlüssige Verbindung zwischen Bremse und Fahrweg wirkt, etwa bei einer Zahnradbahn.
Bei einer Radbremse ist zu unterscheiden, ob die Bremsanlage genug Drehmoment entwickeln kann, um das abzubremsende Rad festzubremsen (Stillstand des Rades) oder ob dies nicht möglich ist. Ist dies nicht möglich, hat die Masse auch hier einen entscheidenden Einfluss auf den Bremsweg. Ist das Drehmoment der Bremse jedoch so groß, dass es das Rad festbremsen kann, besitzt die Masse nur einen geringen Einfluss auf den Bremsweg. Sie erhöht zwar die Trägheit, aber in nahezu gleichem Maße steigt auch die Reibung zwischen Fahrzeug und Untergrund. Allerdings treten aufgrund von Veränderungen im Bereich der Verzahneffekte zwischen Reifen und Fahrbahn, sowie infolge der Abhängigkeit des Haftreibkoeffizienten von der Flächenpressung nichtlineare Haftreibungsverläufe auf, die dazu führen, dass ein leichteres Fahrzeug bei sonst gleichen Bedingungen einen etwas kürzeren Bremsweg aufweist.
Anhalteweg
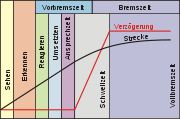
Der Anhalteweg ist die Strecke, die ein Fahrzeug vom Zeitpunkt des Auftretens eines Hindernisses bis zum Stillstand zurücklegt. Das Erkennen dauert in der Regel ca. 0,1 s (einen Augenblick). Die Reaktionszeit liegt bei 0,8 s. Die Bremsansprechzeit, auch Schwellzeit genannt (siehe Abbildung), ist die Zeit, die die Bremsen benötigen, um die maximale Bremswirkung zu entfalten. Bei einer hydraulischen Bremsanlage liegt die Zeit zwischen 0,1 und 0,2 Sekunden, bei der Druckluftbremsanlage zwischen 0,2 und 0,6 Sekunden.
Bei einem Autofahrer wird für die Reaktions- und Vorbremszeit die Dauer von einer Sekunde angenommen. Bei aufmerksamen, geübten Fahrern ist sie kürzer. Drogen, Alkohol und Medikamente verlängern sie deutlich. Die Reaktionszeit bestimmt maßgeblich die Länge des Sicherheitsabstands.
Berechnungen und physikalische Hintergründe
Ist v0 die Anfangsgeschwindigkeit in m/s und a die konstante Bremsverzögerung in m/s², dann beträgt der Bremsweg sB (in m):
- (1)
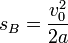
Herleitung dieser Formel:Für die Geschwindigkeit während des Bremsvorganges gilt:
- (2)
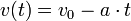
Dabei ist
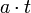 der Teil der Geschwindigkeit, der durchs Bremsen, also Beschleunigen nach hinten, verloren gegangen ist.
der Teil der Geschwindigkeit, der durchs Bremsen, also Beschleunigen nach hinten, verloren gegangen ist.Für die zurückgelegte Wegstrecke gilt:
- (3)
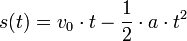
Erklärung dazu:
-
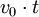 ist die Strecke, die der Gegenstand zurückgelegt hätte, wenn er nicht gebremst worden wäre.
ist die Strecke, die der Gegenstand zurückgelegt hätte, wenn er nicht gebremst worden wäre.
-
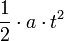 ist dann das,was er durchs Bremsen verloren hat.
ist dann das,was er durchs Bremsen verloren hat.
Der Gegenstand kommt schließlich zum Stillstand, wenn v(t) = 0 ist.
Dies setzt man nun in Gleichung (2) ein:
Löst man diese Gleichung nach der Zeit t auf, erhält man als Bremszeit tB:
Setzt man die Bremszeit tB nun in Gleichung (3) ein, so erhält man die Formel für den Bremsweg:
Für die Bremsverzögerung a gilt dabei wegen der Grundgleichung der Mechanik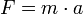 :
:-
- (4)
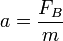
- (4)
Hierbei ist FB die bremsende Kraft und m die Masse des gebremsten Gegenstandes.
Kommt die bremsende Kraft FB durch Gleitreibung (Oberflächen verrutschen gegeneinander; bei einem Auto, wenn die Räder blockieren) auf einem waagrechten Untergrund zustande, so gilt:
-
- (5)
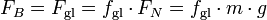
- (5)
Dabei ist fgl die sog. Gleitreibungszahl und g die Erdbeschleunigung (
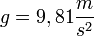 ).
).Die Gleitreibungszahl fgl hängt von der Rauigkeit, etc. der reibenden Oberflächen ab (z.B. Reifen auf trockener Straße: fgl = 0,5).
Setzt man Gleichung (5) in Gleichung (4) ein, so erhält man:
Das bedeutet, dass in der Theorie die Bremsbeschleunigung und damit der Bremsweg unabhängig von der Masse ist.
In der Praxis verursacht jedoch eine höhere Masse eine größere Gleitreibungskraft Fgl. Dadurch entsteht an dem Reifen mehr Hitze, was ihn schneller zum Schmelzen bringt. Der Reifen rutscht dann auf einem Schmierfilm und der Bremsweg wird länger.
Bei einer Bremsverzögerung von ca. 3,86 m/s² (tritt in der Realität auf, wenn ein Auto mit blockierenden Rädern auf einer leicht feuchten Straße bremst) folgt als Faustformel für den Bremsweg (v in km/h, s in m):Zu beachten ist, dass dies keine Formel im physikalischen Sinn ist; denn hier wird nur mit den Maßzahlen gerechnet.
Die Maßeinheiten stimmen in dieser Gleichung nicht (linke Seite Maßeinheit Meter, rechte Seite Maßeinheit
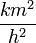 ).
).Eine physikalische Größe MUSS aber immer aus Maßzahl und Maßeinheit bestehen.
Die Bremsverzögerung eines LKW ist um ca. 20 % geringer.Der Reaktionsweg rR hat eine Länge von (tR: Reaktionszeit):
- (6)
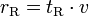 .
.
Der Anhalteweg rA ist die Summe aus Reaktionsweg und Bremsweg:
- (7) rA = rR + sB
Anhaltswerte für Bremsverzögerung in m/s²:
- Trockene Asphaltdecke: 8
- Nasse Asphaltdecke: 6
- Betonfahrbahn: 4-7
- Sand: 4-5
- Schneebedeckte Fahrbahn: 1-3
Bremsen auf der schiefen Ebene
Im Folgenden gehen wir wie oben davon aus, dass der Gegenstand durch Gleitreibung gebremst wird.
BergaufBergauf bremsen den Gegenstand dann die Gleitreibungskraft Fgl und die Hangabtriebskraft FH.
Somit gilt hier für die bremsende Kraft FB:
-
- FB = Fgl + FH
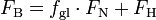
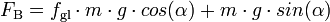
Für die Bremsverzögerung a gilt dann wegen der Grundgleichung der Mechanik
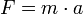 :
:-
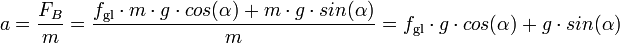
- (8)
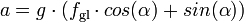
Wie oben gilt für den Bremsweg sB:- (1)
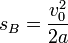
Setzt man Gleichung (8) in Gleichung (1) ein, erhält man
BergabBergab wirkt die Gleitreibungskraft Fgl bremsend und die Hangabtriebskraft FH beschleunigend.
Insgesamt wird der Gegenstand deshalb von der Differenz von Gleitreibungskraft Fgl und Hangabtriebskraft FH gebremst.
Somit gilt hier für die bremsende Kraft FB:
-
- FB = Fgl − FH
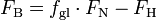
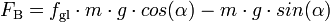
Für die Bremsverzögerung a gilt dann wegen der Grundgleichung der Mechanik
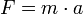 :
:-
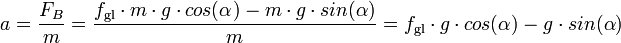
- (9)

Sollte die Hangabtriebskraft FH größer sein als die Gleitreibungskraft Fgl, dann wird der Gegenstand nicht gebremst, sondern schneller. Einen Bremsweg zu berechnen macht dann natürlich keinen Sinn.
Ansonsten gilt wie oben für den Bremsweg sB:- (1)
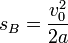
Setzt man Gleichung (9) in Gleichung (1) ein, erhält man
Siehe auch
Weblinks
- (1)
Wikimedia Foundation.