- Schiefe Ebene
-
Eine schiefe, schräge oder geneigte Ebene (kurz rsp. umgangssprachlich: Hang, Schiefe, Schräge bzw. Neigung) ist in der Mechanik eine ebene Fläche, die gegen die Horizontale geneigt ist. Sie wird verwendet, um den Kraftaufwand zur Höhenveränderung einer Masse zu verringern. Der Arbeitsaufwand bleibt jedoch unverändert. Die schiefe Ebene gehört wie der Flaschenzug und die Schraube zu den einfachen Maschinen.
Bei einer schiefen Ebene mit einem Neigungswinkel
 von 45° (entsprechend einem Anstieg von 100 %) verlängert sich die Strecke zum Heben eines Gewichts von z. B. 10 m in der Senkrechten auf etwa 14,1 m entlang der schiefen Ebene, wodurch sich der Kraftaufwand (unter Vernachlässigung der Reibung) auf 71 % reduziert. Wird der Neigungswinkel auf 22,5° (gleich einer Steigung von 41,5 %) halbiert, verlängert sich die Strecke
von 45° (entsprechend einem Anstieg von 100 %) verlängert sich die Strecke zum Heben eines Gewichts von z. B. 10 m in der Senkrechten auf etwa 14,1 m entlang der schiefen Ebene, wodurch sich der Kraftaufwand (unter Vernachlässigung der Reibung) auf 71 % reduziert. Wird der Neigungswinkel auf 22,5° (gleich einer Steigung von 41,5 %) halbiert, verlängert sich die Strecke  auf rund 22 m, der Kraftaufwand verringert sich auf rund 45 % im Vergleich zum direkten Heben.
auf rund 22 m, der Kraftaufwand verringert sich auf rund 45 % im Vergleich zum direkten Heben.Inhaltsverzeichnis
Alltag
Anwendungen dieses Prinzips finden sich bspw. bei Serpentinen im Gebirge, Rampen, die im Altertum zur Errichtung von Gebäuden benutzt wurden, Fahrrad- oder Rollstuhlrampen usw. Schrauben lassen sich auch als Zylinder mit einer aufgewickelten schiefen Ebene betrachten.
Das Werkzeug Keil nutzt ebenfalls die Prinzipien der schiefen Ebene.
Physikalische Grundlagen
Im Folgenden wird die Situation einer ruhenden Masse im Gleichgewicht auf einer schiefen Ebene beschrieben.
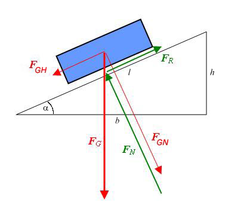
Die Gewichtskraft
 einer Masse, die sich auf einer schiefen Ebene befindet, hat ihren Angriffspunkt im Schwerpunkt der Masse. Sie wird zur Beschreibung des Problems in zwei Komponenten zerlegt, die Hangabtriebskomponente der Gewichtskraft
einer Masse, die sich auf einer schiefen Ebene befindet, hat ihren Angriffspunkt im Schwerpunkt der Masse. Sie wird zur Beschreibung des Problems in zwei Komponenten zerlegt, die Hangabtriebskomponente der Gewichtskraft  parallel zur Oberfläche der schiefen Ebene und die Normalkomponente der Gewichtskraft
parallel zur Oberfläche der schiefen Ebene und die Normalkomponente der Gewichtskraft  senkrecht zur Oberfläche. Es ist strikt zu unterscheiden zwischen den echt wirkenden Kräften und der Zerlegung der Gewichtskraft in zwei Komponenten – die Komponenten sind keine wirkenden Kräfte. Die Normalkraft
senkrecht zur Oberfläche. Es ist strikt zu unterscheiden zwischen den echt wirkenden Kräften und der Zerlegung der Gewichtskraft in zwei Komponenten – die Komponenten sind keine wirkenden Kräfte. Die Normalkraft  welche von unten auf die Masse wirkt, ist eine Kontaktkraft und steht senkrecht zur Ebene. Ihr Angriffspunkt ist nicht im Schwerpunkt der Kontaktfläche, da der Druck nicht konstant ist. Der Betrag der Normalkraft
welche von unten auf die Masse wirkt, ist eine Kontaktkraft und steht senkrecht zur Ebene. Ihr Angriffspunkt ist nicht im Schwerpunkt der Kontaktfläche, da der Druck nicht konstant ist. Der Betrag der Normalkraft  ist gleich dem Betrag der Normalkomponente der Gewichtskraft
ist gleich dem Betrag der Normalkomponente der Gewichtskraft  Eine weitere Kraft, die wirkt, ist die Haftreibungskraft
Eine weitere Kraft, die wirkt, ist die Haftreibungskraft  Auch diese ist eine Kontaktkraft und greift im Schwerpunkt der Kontaktfläche an – ist jedoch parallel zur Ebene und entgegengesetzt der Richtung der Hangabtriebskomponente der Gewichtskraft
Auch diese ist eine Kontaktkraft und greift im Schwerpunkt der Kontaktfläche an – ist jedoch parallel zur Ebene und entgegengesetzt der Richtung der Hangabtriebskomponente der Gewichtskraft 
Damit der Körper in Ruhe bleibt, muss die Hangabtriebskraft
 kleiner sein als die maximal mögliche Haftreibungskraft
kleiner sein als die maximal mögliche Haftreibungskraft  Letztere ist durch den Haftreibungskoeffizient
Letztere ist durch den Haftreibungskoeffizient  und dem Betrag der Normalkraft
und dem Betrag der Normalkraft  gegeben. Es gilt:
gegeben. Es gilt:Ist diese Bedingung nicht erfüllt (weil bspw. der Neigungswinkel der Ebene zu groß ist oder der Haftreibungskoeffizient
 zu klein), beginnt die Masse zu rutschen.
zu klein), beginnt die Masse zu rutschen.Hat die Masse eine Geschwindigkeit oder wirken noch weitere Kräfte, so müssen zusätzliche Überlegungen und Fallunterscheidungen gemacht werden, die hier noch nicht beschrieben sind. Die detaillierte mathematische Beschreibung der ruhenden Masse auf der schiefen Ebene ist im nächsten Abschnitt festgehalten.
Körper in Ruhe
Folgende Bezeichnungen werden verwendet:
 = Gewichtskraft der Masse,
= Gewichtskraft der Masse, = Normalkomponente der Gewichtskraft
= Normalkomponente der Gewichtskraft 
 = Normalkraft,
= Normalkraft, = Hangabtriebskomponente der Gewichtskraft
= Hangabtriebskomponente der Gewichtskraft 
 = Haftreibungskraft,
= Haftreibungskraft, = Neigungswinkel der schiefen Ebene,
= Neigungswinkel der schiefen Ebene, = Haftreibungs-Koeffizient,
= Haftreibungs-Koeffizient,
- (
 = Gleitreibungskoeffizient)
= Gleitreibungskoeffizient)
- (
 = Höhe der schiefen Ebene,
= Höhe der schiefen Ebene, = Basis der schiefen Ebene sowie
= Basis der schiefen Ebene sowie = Länge der schiefen Ebene.
= Länge der schiefen Ebene.
Die Gewichtskraft
 kann aufgeteilt werden in eine Komponente senkrecht zur schiefen Ebene (Normalkomponente
kann aufgeteilt werden in eine Komponente senkrecht zur schiefen Ebene (Normalkomponente  ) und eine Komponente parallel zur schiefen Ebene (Hangabtriebskomponente
) und eine Komponente parallel zur schiefen Ebene (Hangabtriebskomponente  ).
).An der Kontaktfläche zwischen Körper und schiefer Ebene wirken eine Normalkraft
 und eine Haftreibungskraft
und eine Haftreibungskraft 
Da der Körper in Ruhe ist, muss die Haftreibungskraft FR gerade gleich groß oder größer sein wie die Hangabtriebskomponente
 der Gewichtskraft:
der Gewichtskraft:Mit dem Haftreibungsgesetz:
ergibt sich als notwendige Bedingung:
Wenn der Neigungswinkel
 zu groß oder der Reibungskoeffizient
zu groß oder der Reibungskoeffizient  zu klein ist, so ist kein Gleichgewicht möglich der Körper rutscht.
zu klein ist, so ist kein Gleichgewicht möglich der Körper rutscht.Der Haftreibungskoeffizient
 (manchmal als
(manchmal als  bezeichnet) ist in jedem Fall größer als der Gleitreibungskoeffizient
bezeichnet) ist in jedem Fall größer als der Gleitreibungskoeffizient 
Zu beachten ist, dass:
bezeichnet wird.
Bewegung mit Luftwiderstand
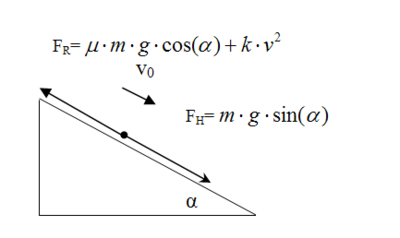
Im Folgenden soll die Luftwiderstandskraft
 bei der Bewegung des Körpers an der schiefen Ebene berücksichtigt werden. Im Gegensatz zu obigem Abschnitt ist der Körper nicht mehr in Ruhe. Wirksam ist der Luftwiderstand sowie die Gleitreibung. Die Konstante
bei der Bewegung des Körpers an der schiefen Ebene berücksichtigt werden. Im Gegensatz zu obigem Abschnitt ist der Körper nicht mehr in Ruhe. Wirksam ist der Luftwiderstand sowie die Gleitreibung. Die Konstante  ist von der Form des Körpers und der Dichte des strömenden Mediums (bspw.: Luft) abhängig. Es gilt:
ist von der Form des Körpers und der Dichte des strömenden Mediums (bspw.: Luft) abhängig. Es gilt:Hierbei ist:
 = der Widerstandsbeiwert,
= der Widerstandsbeiwert, = die Körperquerschnittsfläche,
= die Körperquerschnittsfläche, = die Dichte des strömenden Mediums sowie
= die Dichte des strömenden Mediums sowie = der Gleitreibungs-Koeffizient.
= der Gleitreibungs-Koeffizient.
Aus den Kraftansätzen entstehen recht komplexe Bewegungsgleichungen – diese Differenzialgleichungen sind jedoch lösbar.
Abwärtsbewegung
Aus dem Kraftansatz:
folgt die Differenzialgleichung:
mit:
Folgende Fälle sind zu unterscheiden:
- a)
Ansatz:Durch Einsetzen in die Differenzialgleichung erhält man unter Berücksichtigung von:
und durch Koeffizientenvergleich:
 und
und 
Als Lösung ergibt sich:
![\dot{\vec v} = \sqrt{\frac{c}k} \tanh \left[\frac{t \sqrt{c k}}m + \operatorname{Artanh}\left(\vec v_0 \sqrt{\frac{k}c} \right) \right]\, .](4/634ad1b42565f353949a93ed9b44aa74.png)
 ist die Endgeschwindigkeit.
ist die Endgeschwindigkeit.
 ist der Tangens Hyperbolicus.
ist der Tangens Hyperbolicus.
- b)
 bzw.
bzw. 
Unter Berücksichtigung von itanh ix = − tan x erhält man:
Zum Zeitpunkt
 kommt der Körper zur Ruhe.
kommt der Körper zur Ruhe.Für den Bremsweg
 gilt:
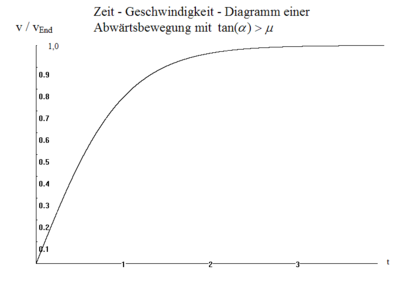
gilt:- c)
 bzw.
bzw. 

Die Geschwindigkeit nähert sich zwar hyperbelförmig der Ruhe, der Bremsweg ist aber unendlich lang.
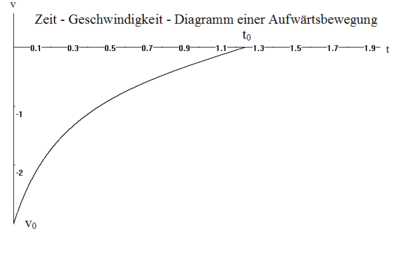
Aufwärtsbewegung
Aus dem Kraftansatz:
folgt die Differenzialgleichung:
mit:
Ansatz:
Durch Einsetzen in die Differenzialgleichung erhält man unter Berücksichtigung von:
und durch Koeffizientenvergleich erhält man:
 und
und 
Als Lösung ergibt sich:
zum Zeitpunkt:
kommt der Körper zur Ruhe, wobei
 negativ ist.
negativ ist.Für den Bremsweg
 gilt:
gilt:Weblinks
Wikimedia Foundation.















![\dot{\vec v} = - \sqrt{- \frac{c}k} \tan \left(\frac{\sqrt{- c k}}m \left(t - t_0 \right) \right); t \in \left[{0; t_0} \right]\, .](5/5352b0eec356cc851264d93261d6d4a1.png)

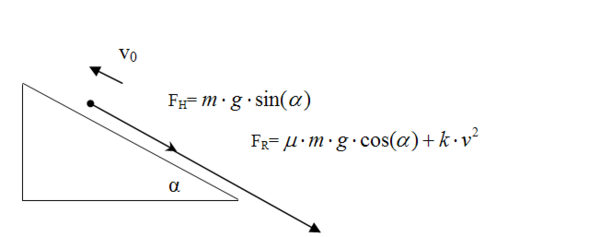






![\dot{\vec v} = \sqrt{\frac{c}k} \tan \left(\frac{{\sqrt{c k}}}m \left(t - t_0 \right) \right); t \in \left[{0; t_0} \right]](3/aa324604a08bebce6d7ae6cd166e5082.png)

![\vec s = \int\limits_0^{t_0} {\dot{\vec v} t\, \mathrm{d} t = - \frac{m}k \ln \left(\cos \left[\arctan \left(\left| \vec v_0 \right| \sqrt{\frac{k}c} \right) \right] \right)}\, .](c/02c27a32659306ae62ac5f0062a57656.png)