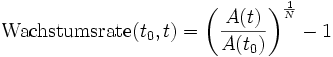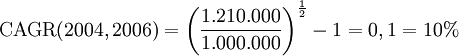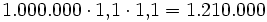Wachstumskonstante

Als Wachstumsrate bezeichnet man die durchschnittliche relative Zunahme einer Größe pro Zeiteinheit. Dabei wird ein exponentieller Vorgang angenommen. Statt der Wachstumsrate wird in der Mathematik meist mit der Wachstumskonstante λ gerechnet. Eine Wachstumsrate von 23 % also 0,23 pro Jahr entspricht dabei λ=1,23/Jahr.

Die Wachstumsrate wird durch die allgemeine Gleichung

$\mathrm{Wachstumsrate}(t_0,t) = \left( \frac{A(t)}{A(t_0)} \right)^\frac{1}{N} - 1$

ausgedrückt, wobei N=t-t₀ die Anzahl der Zeiteinheiten zwischen t₀ und t und A(t) die betrachtete Größe zum jeweiligen Zeitpunkt t darstellt.

Compound Annual Growth Rate

Eine spezielle Wachstumsrate ist die jährliche Wachstumsrate (engl. Compound Annual Growth Rate, abgekürzt CAGR). Sie stellt das durchschnittliche jährliche Wachstum einer zu betrachtenden Größe dar. Zur Berechnung wird der aktuelle Wert durch den Ausgangswert geteilt. Von dem Ergebnis wird die n-te Wurzel gezogen, wobei n = die Anzahl der Jahre ist, die betrachtet werden. Die Compound Annual Growth Rate stellt also den durchschnittlichen Prozentsatz dar, um den der Anfangswert einer Zeitreihe auf hypothetische Folgewerte für die Berichtsjahre wächst, bis der tatsächliche Endwert am Ende der Berichtsperiode erreicht ist. Tatsächliche Ausschläge der Folgejahre in der Zwischenzeit wirken sich dabei nicht aus.

In der Betriebswirtschaft und Volkswirtschaft ist die CAGR eine wesentliche Kennziffer zur Betrachtung von Investitionen, Marktentwicklungen, Umsätzen etc.

Die Formel für die CAGR ist dieselbe wie die der Wachstumsrate, wobei bei CAGR die Größe N als Anzahl von Jahren ausgedrückt wird.

Beispiel: Eine Firma erzielt im Jahr 2004 einen Umsatz von 1 Million €. Im Jahr 2006 beträgt der Umsatz 1,21 Millionen €. Die Anzahl der Zeiteinheiten N beträgt 2006 - 2004 = 2.

$\mathrm{CAGR}(2004,2006) = \left( \frac{1.210.000}{1.000.000} \right)^\frac{1}{2} - 1 = 0,1 = 10%$

Die jährliche Wachstumsrate beträgt 10 %. Wenn man daher den Ausgangswert zweimal mit 1,1 multipliziert erhält man den Endwert:

$1.000.000 \cdot 1{,}1 \cdot 1{,}1 = 1.210.000$

Verdopplungszeit

Die Zeitspanne, in der sich die Bevölkerung eines Landes verdoppelt, nennt man Verdopplungszeit. Sie entspricht dem Quotient aus der Zahl 70 und der Wachstumsrate des Landes.

Spezifische Wachstumsrate in der Biotechnologie

Bei exponentiellem Wachstum ist die Geschwindigkeit der Veränderung der Zellmasse (dX/dt) zu jedem Zeitpunkt proportional zur Zellmasse X. Die Proportionalitätskonstante wird als spezifische Wachstumsrate µ bezeichnet.

dX/dt = µ X