Wachstum

Verschiedene Arten von Wachstum.

• Exponentielles Wachstum
• Lineares Wachstum
• Kubisches Wachstum

Wachstum bezeichnet die Zunahme einer bestimmten Messgröße im Zeitverlauf. Das Gegenteil von Wachstum ist die Schrumpfung, also die Abnahme einer Messgröße. In diesem Zusammenhang fällt oft der von der mathematischen Modellierung abgeleitete und umgangssprachlich oft missverstandene Begriff Negativwachstum.

Mathematische Beschreibung

Wachstum ist das zeitliche Verhalten einer System-Messgröße. Zunächst wird zu einem bestimmten Zeitpunkt t₁ der Wert W₁ dieser Größe bestimmt. Zu einem späteren Zeitpunkt t₂ wird wieder der Wert dieser Größe, diesmal W₂, bestimmt.

Ist dieser zweite Wert größer als der erste, also W₂ > W₁, dann spricht man von positivem Wachstum. Das entspricht dem allgemeinen Sprachgebrauch.

Ist der zweite Wert jedoch kleiner als der erste, also W₂ < W₁, spricht man von negativem Wachstum.

Im Falle W₂ = W₁ spricht man von Nullwachstum.

Darstellung von Wachstumskurven

Bei zahlreichen Messpunkten werden diese zur Veranschaulichung in einem Diagramm dargestellt, meistens als geschlossener Kurvenzug. Dabei sollte aber nicht vergessen werden, dass das tatsächliche Verhalten des Systems zwischen den Messpunkten wegen der Zeitdiskretisierung nicht bekannt ist und höchstens durch ein mehr oder weniger genaues Modell beschreibbar ist. Bei bestimmten Wachstumsarten können auch mathematische Modelle (Funktionen) zur Beschreibung des Verhaltens in einem Funktionsgraph Verwendung finden.

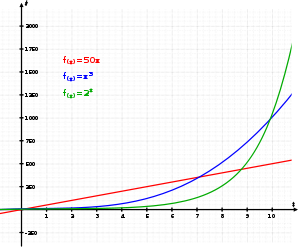
Wachstumsarten

linear

Ein Wachstum heißt linear, wenn die Änderungsrate k konstant ist.

Bei linearem Wachstum gilt für den Bestand B(t) nach t Zeitschritten :

• rekursive Darstellung:

B(t + 1) = B(t) + k mit Anfangsbestand B(0) und Änderungsrate k

• explizite Darstellung:

$B(t) = k \cdot t + B(0)$

• Differentialgleichung:

$\, B'(t) = k$

exponentiell

Ein Wachstum heißt exponentiell, wenn die Änderungsrate $k\cdot B(t)$ nicht konstant, sondern proportional zum Bestand $\, B(t)$ ist.

• rekursive Darstellung:

$B(t+1) = B(t)+k \cdot B(t)=(1+k) \cdot B(t)=a \cdot B(t)$

(a = 1 + k wird als Wachstumsfaktor bezeichnet)

• explizite Darstellung:

$B(t) = B(0) \cdot a^t = B(0) \cdot (1+k)^t = B(0) \cdot e^{\widehat{k} \cdot t}\,$, mit $\widehat{k} = \ln(1+k)$

• Differentialgleichung:

$B'(t) = \widehat{k} \cdot B(t)$

beschränkt

Ein Wachstum heißt beschränkt mit der Schranke (Kapazität) $\, S$, wenn die Änderungsrate B(t + 1) − B(t) bzw. $\,B'(t)$ nicht konstant, sondern proportional zum Sättigungsmanko $\, S - B(t)$ ist.

• rekursive Darstellung:

$B(t+1) = B(t)+k \cdot (S-B(t)) = (1-k) \cdot B(t) + k \cdot S = q \cdot B(t) + c$

• explizite Darstellung:

$B(t)= S - (S-B(0))\cdot q^t= S - (S - B(0)) \cdot (1-k)^t = S-(S-B(0)) \cdot e^{-\widehat{k} \cdot t}\,$ mit $\widehat{k} = -\ln(1-k)$

• Differentialgleichung:

$B'(t)=\widehat{k} \cdot (S - B(t)) = \widehat{k}\cdot S - \widehat{k}\cdot B(t) = \widehat{c} - \widehat{k} \cdot B(t)$

logistisch

Ein Wachstum heißt logistisch mit der Schranke $\,S$, wenn die Änderungsrate $\,B(t+1)-B (t)$ bzw.$\,B'(t)$ nicht konstant, sondern proportional zum Produkt aus Bestand und Sättigungsmanko $B (t) \cdot (S - B(t))$ ist.

• rekursive Darstellung:

$B(t+1) = B(t) + k \cdot B(t) \cdot (S - B(t)) = (1+k \cdot S) \cdot B(t) - k \cdot B(t)^2$

• explizite Darstellung:

$B(t) = \frac{B(0) \cdot S}{B(0)+(S-B(0)) \cdot e^{-k \cdot S \cdot t}}$

• Differentialgleichung:

$B'(t) = k \cdot B(t)\cdot (S - B(t)) = k \cdot S \cdot B(t) - k \cdot B(t)^2$

nach Zeitverlauf

Wachstum lässt sich nach der Art seiner Zeitverläufe charakterisieren, wie er im Graphen Messgröße x vs. Zeit t dargestellt ist.

• begrenzt oder unbegrenzt: Alle realen Wachstumsvorgänge sind letztlich begrenztes Wachstum, da die Ressourcen, aus welchen sich das Wachstum speist, nicht unbegrenzt vorliegen oder das Wachstum auf andere Weise schon vor dem Erschöpfen der Ressourcen begrenzt wird und einem dynamischen Gleichgewicht zustrebt (zum Beispiel beim Räuber-Beute-System). Unbegrenztes Wachstum ist damit ein mathematisches Artefakt. Begrenztes Wachstum führt aber nicht zwingend zu einer Wachstumsumkehr, sondern erlaubt während der Lebensdauer eines Systems innerhalb seiner Wachstumsgrenzen ein auf Dauer positives Wachstum. Das klassische Beispiel ist die Entropie in geschlossenen Systemen. Die maximale Entropie des Systems ist hier die Wachstumsgrenze.
• linear (konstant) oder exponentiell (beschleunigt oder verzögert = negativ beschleunigt) Der Radioaktive Zerfall ist ein Beispiel für exponentielles, verzögertes, negatives Wachstum.
• (scheinbar) kontinuierlich oder diskontinuierlich. (Beispiel: Die Längenzunahme des Menschen während der Wachstumsperiode erfolgt in Schüben.)

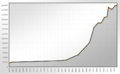
Das abgebildete logistische Wachstum ist als lineare Transformation des hyperbolischen Tangens darstellbar und beschreibt das begrenzte Wachstum einer Größe (z. B. Ressourcen-Konsum, Bevölkerungszuwachs usw.). Das Wachstum hat eine Sättigungsgrenze. Die Größe selbst nimmt aber theoretisch weiter unbegrenzt zu. Das Wachstum dieser Größe ist einer Sigmoid-Kurve mit einem glockenförmigen Verlauf. Die Größe selbst hat nun eine Sättigungsgrenze. Es gibt dann vier Abschnitte: (1) eine theoretisch unendlich lange Periode sehr geringen Wachstums, (2) eine kurze Periode ansteigenden hohen Wachstums, (3) eine kurze Periode sinkenden hohen Wachstums und schließlich wieder (4) eine theoretisch unendlich lange Periode sehr geringen Wachstums.

• 

  Hier beschreibt die logistische Funktion das Wachstum W(t). Der Bestand der wachsenden Größe nähme mit dem Zeitintegral der logistischen Kurve unbegrenzt zu. Häufiger beschreibt die logistische Funktion den Bestand B(t), der ein Maximum nicht überschreiten kann.

• 

  Bevölkerungsentwicklung von Augsburg als Beispiel für ein reales Wachstum, das dem Verlauf der logistischen Funktion nahe kommt.

• 

  Beispiel von Graphen für lineares positives negatives und Nullwachstum

• 

  Beispiel von Graphen für exponentielle positives oder negatives bzw. beschleunigtes oder verzögertes Wachstum

Wachstumsschwankungen

Dem Trend ist eine Schwankung zwischen mehreren Grenzwerten überlagert:

• Periodische Schwankungen (beispielsweise bei Systemen mit Rückkopplung) können ungedämpft, gedämpft oder aufschaukelnd sein.
• Aperiodische Schwankungen (Fluktuationen) können zufallsbedingt oder chaotisch sein.

Nach Einheiten der Messgröße

Raumdimensionen

Strecken 

Wachstum der Länge des Schienennetzes

Flächen 

Wachstum der versiegelten Flächen

Volumen 

Größerwerden eines Luftballons

Kombinationen daraus findet man beim Wachstum eines Organismus als Ganzes oder seiner Teile: Zellwachstum, Längenwachstum des Menschen; siehe auch Somatotropin (Wachstumshormon) und Kleinwuchs.

Anzahl

Zunahme der absoluten Menge oder des Prozentsatzes, Vermehrung: Bevölkerungswachstum, Bakterienkultur, Geldwachstum.

Das Infekt-Modell ist eine Rückkopplungsfunktion, die Ausbreitungsvorgänge (Krankheiten, Gerüchte, Witze …) in geschlossenen Populationen beschreibt (s. Bild begrenztes Wachstum). Siehe auch Feigenbaumdiagramm.

Wachstum eines Index

Wirtschaftswachstum beschreibt das Wachstum einer Volkswirtschaft. Parametrisiert wird dieses u. a. durch das Bruttoinlandsprodukt.

Wachstum beschreibt in der Betriebswirtschaftslehre das Wachstum von Kapazitäten. Parametrisiert wird dieses u.a. durch den Engpass an einem bestimmten Produktionsfaktor. Dieser hat in einem Operations Research System einen Schattenpreis.

Wachstum der Komplexität

Siehe dazu Internet, Informationsflut, Gehirn

Anwendungsgebiete

Biologisches Wachstum

In der Physiologie ist das Wachstum durch die Differenz zwischen anabolem Ansatz und katabolem Abbau definiert. Man spricht von Wachstum, wenn die Größe eines Organismus zunimmt, ohne dass sich dessen äußere Gestalt ausschlaggebend verändert.

Wachstum kommt zustande durch:

• Hyperplasie: die Anzahl der Zellen eines Organismus nimmt zu
• Hypertrophie: die Größe von Zellen nimmt zu
• die extrazelluläre Matrix gewinnt an Größe

Vergleiche auch Wachstumsstörung, Atrophie.

Menschliches Wachstum

Beim Menschen und anderen Individuen findet körperliches Wachstum lediglich in der Kindheit statt. Im Erwachsenenalter (Erwachsener) spricht man von Homöostase, wenn anabole und katabole Prozesse im Gleichgewicht stehen. Wird zu viel Energie zugeführt, wird diese in Form von Fett gespeichert, so dass zwar die Größe des lebenden Körpers weiter zunimmt, jedoch in unästhetischer Form (Zivilisationskrankeit Adipositas).

Wachstum von Arten

Die Evolutionstheorie (Darwin) untersucht die Entwicklung von Arten und stellt diese als Ergebnis von Wachstum der Art (Überproduktion von Nachkommen) und Selektion dar.

Wirtschaft

Unter Wirtschaftswachstum versteht man die Änderung des Bruttoinlandsprodukts (BIP) von einer Periode zur nächsten, siehe Hauptartikel Wirtschaftswachstum.

Siehe auch

• Diffusionsbegrenztes Wachstum (diffusion limited aggregation)
• Nullwachstum
• Enquete-Kommission Wachstum, Wohlstand, Lebensqualität – Wege zu nachhaltigem Wirtschaften und gesellschaftlichem Fortschritt in der Sozialen Marktwirtschaft

Literatur

• Rupert Riedl, Manuela Delpos (Hrsg.): Die Ursachen des Wachstums. 1996, ISBN 3-218-00628-7.
• Johannes M. Waidfeld: Wachstum, der Irrtum Wohlstand, eine gesellschaftliche Betrachtung. Fischer & Fischer Medien AG, Frankfurt 2005, ISBN 3-89950-076-8, http://www.waidfeld.de/
• Ernest Mandel: Marxistische Wirtschaftstheorie. Suhrkamp Verlag, Frankfurt 1968

Weblinks

 Wiktionary: Wachstum – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

 Wiktionary: wachsen – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

 Wikiquote: Wachstum – Zitate

• Analyse von Wachstumsvorgängen
• lineares, exponentielles, beschränktes und logistisches Wachstum