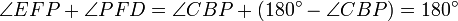Wallace-Gerade

Simson-Gerade

Liegen die Fußpunkte eines Punktes P auf die (eventuell verlängerten) Seiten eines Dreiecks 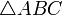$\triangle ABC$ auf einer gemeinsamen Geraden, so wird diese Gerade als simsonsche Gerade oder wallacesche Gerade und der Punkt P als ihr Pol bezeichnet. Dies ist genau dann der Fall, wenn P auf dem Umkreis von 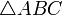$\triangle ABC$ liegt.

Die Simson-Gerade ist irrtümlicherweise nach dem Mathematiker Robert Simson benannt, in dessen Werk sich jedoch keine Arbeit zur Simson-Gerade finden lässt. In Wirklichkeit wurde sie 1797 von William Wallace entdeckt.^[1]

Weitere Eigenschaften

Parallele zur Simson-Gerade

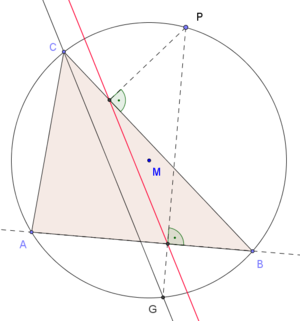
Simson-Gerade ist parallel zu GC Jede Simson-Gerade eines Dreieckes besitzt drei besondere Parallelen, die jeweils durch einen der drei Eckpunkte des Dreiecks verlaufen. Genauer gesagt gilt der folgende Satz: Gegeben sind ein Dreieck 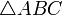$\triangle ABC$, ein Punkt P auf seinem Umkreis und die zugehörige Simson-Gerade. Ist G nun der Schnittpunkt des Lotes von P auf AB mit dem Umkreis, dann ist die Gerade CG parallel zur Simson-Gerade.[1]

Schnittwinkel zwischen Simson-Geraden

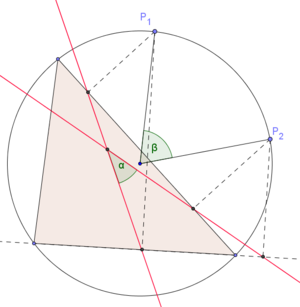
2α = β Betrachtet man bei einem Dreieck zwei unterschiedliche Punkte auf dessen Umkreis, so erhält man zwei verschiedene Simson-Geraden. Der Schnittwinkel dieser beiden Simson-Geraden ist genau halb so groß wie der Winkel, den die beiden Punkte mit dem Mittelpunkt des Umkreises bilden. Es seien P1 und P2 zwei Punkte auf dem Umkreis von 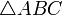$\triangle ABC$ mit Mittelpunkt M. Weiterhin sei α der Schnittwinkel der beiden zugehörigen Simson-Geraden und 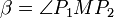$\beta=\angle P_1MP_2$. Dann gilt 2α = β.[1]

Simson-Gerade als Streckenhalbierende

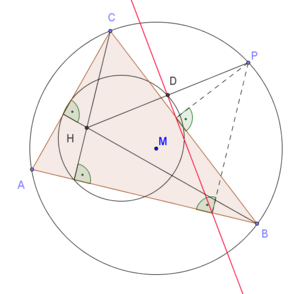
| HD | = | DP | Verbindet man den Höhenschnittpunkt eines Dreiecks mit einem Punkt auf dem Umkreis des Dreiecks, so wird diese Verbindungsstrecke von der zugehörigen Simson-Geraden halbiert. Gegeben sind ein Dreieck 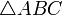$\triangle ABC$, ein Punkt P auf seinem Umkreis und die zugehörige Simson-Gerade. Ist H der Höhenschnittpunkt von 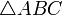$\triangle ABC$, dann schneidet die Simson-Gerade die Strecke 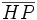$\overline{HP}$ in D und es gilt | HD | = | DP | . Außerdem liegt D auf dem Feuerbachkreis.[1] [2]

Geradenschar

Simson-Geraden als Tangenten einer Deltoide Lässt man den Simson-Pol P auf dem Kreis wandern, dann besitzt die so entstehende Geradenschar von Simson-Geraden eine Deltoide, auch als Steiner-Hypozykloide bezeichnet, als Hüllkurve. [1] [2]

Sonstiges

Besitzen zwei Dreiecke denselben Umkreis und ihre zugehörigen Simson-Geraden denselben Pol, so ist der Schnittwinkel der beiden Simson-Geraden unabhängig von der Wahl des Pols. Mit anderen Worten: Für alle Punkte P auf dem gemeinsamen Umkreis der beiden Dreiecke ergibt sich ein gleich großer Schnittwinkel der beiden zugehörigen Simson-Geraden.

Beweis

Bewiesen wird: Liegt P auf dem Umkreis von 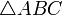$\triangle ABC$, so liegen die Fußpunkte auf einer gemeinsamen Geraden. Dazu zeigt man, dass 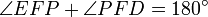$\angle EFP + \angle PFD = 180^\circ$ gilt.

Die Fußpunkte E und F liegen auf dem Thaleskreis über [PA]. Da Umfangswinkel (Peripheriewinkel) über demselben Kreisbogen gleich groß sind, folgt

$\angle EFP = \angle EAP = 180^\circ - \angle PAC$.

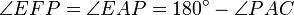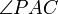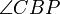Andererseits ist PBCA voraussetzungsgemäß ein Sehnenviereck. Die gegenüberliegenden Winkel $\angle PAC$ und $\angle CBP$ dieses Vierecks ergänzen sich daher zu 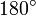$180^\circ$. Insgesamt ergibt sich also

$\angle EFP = \angle CBP$.

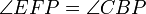Die Punkte D und F liegen auf dem Thaleskreis über [PB], sodass auch PBDF ein Sehnenviereck ist. Ähnlich wie vorher schließt man 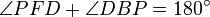$\angle PFD + \angle DBP = 180^\circ$. Wegen 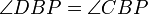$\angle DBP = \angle CBP$ erhält man daraus

$\angle PFD = 180^\circ - \angle CBP$.

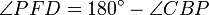Damit ist mit

$\angle EFP + \angle PFD = \angle CBP + (180^\circ - \angle CBP) = 180^\circ$

die Behauptung bewiesen.

Bemerkung: Der angegebene Beweis bezieht sich auf die in der Skizze dargestellte Lage der Höhenfußpunkte. Liegen diese anders, muss die Begründung entsprechend variiert werden.

Einzelnachweise

1. ↑ ^{a b c d e} Coxeter, H. S. M. and Greitzer, S. L. "Simson Lines." §2.5 in Geometry Revisited. Washington, DC: Math. Assoc. Amer., pp. 41, 1967.
2. ↑ ^{a b} Eric W. Weisstein: Simson-Gerade (engl.) auf MathWorld (englisch)

Literatur

• Max Koecher, Aloys Krieg: Ebene Geometrie, 3. Aufl., Springer-Verlag, Berlin 2007, ISBN 978-3-540-49327-3
• Coxeter, H. S. M., und S. L. Greitzer: Zeitlose Geometrie, Klett Stuttgart 1983
• Eric W. Weisstein: Simson-Gerade (engl.) auf MathWorld (englisch)

Weblinks

• Simsonsche Gerade - eine Visualisierung mit GeoGebra
• Simson-Gerade auf Matroids Matheplanet
• Simson-Gerade auf www.matheraetsel.de

• Simson-Gerade auf cut-the-knot (engl.)
• Artikel zur Simson-Gerade bei der MAA (engl.)