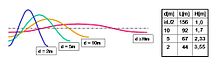
Wellentransformation

Die Transformation (Umformung) fortschreitender Schwerewellen (Wasserwellen) kann vielfältige Ursachen haben. Bei Wellentransformationen sind folgende Effekte zu unterscheiden:

• abnehmende Wassertiefe, vergl. Dispersion (Wasserwellen)
• Reibungseffekte am Meeresboden
• Refraktion
• Diffraktion
• Reflexion
• Wellenbrechen
• überlagerte Strömungen
  • konstante Strömungen
  • beschleunigte Strömungen.

Wellentransformation infolge abnehmender Wassertiefe

Wellenverformung gemäß linearer Wellentheorie für eine Welle der Periode = 10 s, Höhe = 1 m und der Länge L = 156 m; Annahme: Wahrung der Kontinuität.

Wellen mit Längen L (etwa) größer als der 2-fachen Wassertiefe d (L ≥ 2d) unterliegen einer veränderten Dispersion derart, dass die Wassertiefe als Randbedingung hinzu tritt. Während die Wellenfortschrittsgeschwindigkeit c und die Wellenlänge L mit abnehmender Wassertiefe ebenfalls geringer werden, wächst die Wellenhöhe H.

Wellentransformation infolge überlagerter Strömungen

In der Natur liegt im allgemeinen eine Wechselwirkung der Wellenkinematik mit einem weiteren Strömungsfeld vor, dessen Einfluss von keiner bekannten Wellentheorie erfasst wird. Derartig überlagerte Strömungen bewirken nicht nur eine Verformung der Wellen sondern haben u.a. infolge des Doppler-Effektes Einfluss auf die Frequenz und damit auch auf die Dispersion und Transformation der Wellen.

Doppler-Effekt infolge konstanter Strömungsgeschwindigkeit

Unbeschleunigte Strömungen stellen den Sonderfall dar. Unterliegt das Trägermedium der Wellen etwa einer konstanten Strömung, mit einer dem Wellenfortschritt gleich- oder entgegen gerichteten Komponente, so ist die Frequenz bzw. Periode gegenüber einem durch Strömung unbeeinflussten Medium verändert. Ist die Strömungskomponente u_M dem Wellenfortschritt gleichgerichtet, kommen an einem Messort pro Zeiteinheit mehr Wellen an. Dieses bedeutet, dass die Wellenlänge L_A, die bei fehlender Strömung vorhanden wäre, hier um das Verhältnis

$\frac{c_A-u_M}{c_A} \,$

verkürzt als L_B gemessen wird:

$L_B=L_A\cdot\frac{c_A-u_M}{c_A}=L_A\cdot \left(1-\frac{u_M}{c_A}\right) \,$

Für die Frequenz f_B am Messort ergibt sich daher:

$f_B=\frac{c_A}{L_B}=\frac{f_A}{{{1-\frac{u_M}{c_A}}}} \,$

Für eine entgegengesetzt gerichtete Strömungsgeschwindigkeit u_M, sind in den Klammern positive Vorzeichen zu verwenden.

Wellentransformation infolge beschleunigter Strömung

Beschleunigte Strömungen nahe der Wasseroberfläche (Triftströmungen) können auf meteorologische Einflüsse zurückgeführt werden. Durch die Tidebewegung verursachte beschleunigte Strömungen erstrecken sich in Flachmeeren oft über die gesamte Wassertiefe. Ähnliches gilt in Küstennähe für großräumige Rückströmungen (undertow), sog. Rippströmungen und für brandungserzeugte Rückströmungen (backwash). Die letzteren stellen eine wichtige Komponente des Brandungsprozesses dar, da ihr Einfluss auf die Phasengeschwindigkeit insbesondere als Ursache für eine deutliche Frequenz- bzw. Periodenänderung ausbrandender Wellen entlang eines Wellenstrahls angesehen werden kann. Werden unterschiedliche Phasengeschwindigkeiten c entlang eines Wellenstrahls auf eine konvektiv beschleunigte Bewegung des Trägermediums der Wellen zurückgeführt und zugleich Frequenzveränderungen entlang dem Wellenstrahl in Betracht gezogen, kann daraus gefolgert werden, dass an zwei Orten A und B unterschiedliche Wellenanzahlen pro Zeiteinheit vorhanden sind.

Nimmt infolge einer dem Wellenfortschritt entgegengerichteten Strömung die Phasengeschwindigkeit zwischen den Orten A und B von c_A auf c_B ab, so folgt daraus, dass am Ort B in der Zeiteinheit weniger Wellen ankommen, als wenn

$c_B = c_A = \text{konst}. \,$

Beschleunigte Strömung überlagert

Ist die Differenz der Phasengeschwindigkeiten

$\delta c = c_A - c_B \quad \text{bzw.} \quad c_B = c_A - \delta c$

vergrößert sich die Wellenlänge L_A = c_A / f_A auf dem Wege von A nach B um das Verhältnis

$\frac{c_A+\delta c}{c_A} \,$

auf

$L_B = L_A \cdot \frac{c_A + \delta c}{c_A} = \frac{L_A}{c_A} \cdot (c_A + \delta c) = \frac{1}{f_A} \cdot (c_A + \delta c) \,$

Damit ergibt sich die Frequenz am Ort B zu:

$f_B = \frac{c_B}{L_B} = f_A \cdot \frac{c_A - \delta c}{c_A + \delta c} = f_A \cdot \frac{c_B}{2c_A+c_B} < f_A \,$

Die Differenz der Frequenzen wird als Frequenzverschiebung definiert:

$\delta f=f_B-f_A=f_A \cdot \frac{2(c_B-c_A)}{2c_A-c_B} \,$

Demnach kann δf positiv oder negativ sein, je nachdem ob

$2 c_A > c_B > c_A \quad \text{oder} \quad 2c_A < c_B < c_A$