- Doppler'sches Prinzip
-
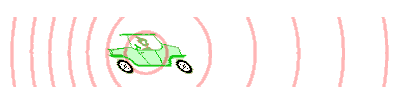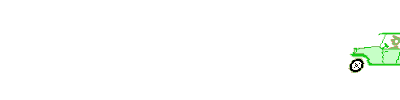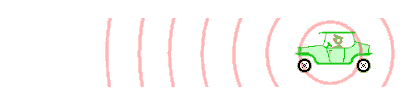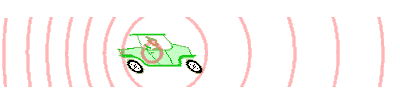
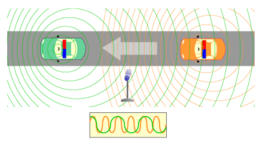
Als Dopplereffekt (auch Doppler-Effekt) bezeichnet man die Veränderung der wahrgenommenen oder gemessenen Frequenz von Wellen jeder Art, während sich die Quelle und der Beobachter einander nähern oder voneinander entfernen, sich also relativ zueinander bewegen.
Nähern sich Beobachter und Quelle einander, so erhöht sich die vom Beobachter wahrgenommene Frequenz, entfernen sie sich von einander, verringert sich die Frequenz. Bekanntes Beispiel ist die Tonhöhenänderung des Martinshorns eines Rettungswagens. Solange sich das Fahrzeug nähert, ist der wahrgenommene Ton höher als im Stand; wenn es sich entfernt, ist er tiefer.
Inhaltsverzeichnis
Entdeckung
Der Dopplereffekt wurde nach dem österreichischen Physiker und Mathematiker Christian Doppler benannt, der ihn 1842 voraussagte. Doppler wollte die unterschiedlichen Farben der Sterne durch ihre Eigenbewegung erklären. Auch wenn er damit falsch lag – die Farben entstehen hauptsächlich durch unterschiedliche Oberflächentemperatur der Sterne – war seine Berechnung im Prinzip richtig.
Ein Experiment zum Dopplereffekt mit Schallwellen wurde 1845 vom Physiker Christoph Buys-Ballot durchgeführt. Er postierte dazu mehrere Trompeter sowohl auf einem fahrenden Eisenbahnzug als auch neben der Bahnstrecke. Beim Vorbeifahren sollte jeweils einer von ihnen ein G spielen und die anderen die gehörte Tonhöhe bestimmen. Trotz Schwierigkeiten bei der Durchführung – das Geräusch der Lokomotive war sehr laut, die Musiker waren manchmal unaufmerksam – gelang es Buys-Ballot, den Dopplereffekt zu bestätigen. Armand Hippolyte Fizeau entdeckte den Effekt für Licht im Jahre 1848.
William Huggins wandte den Dopplereffekt auf Sternbewegungen an.
Begründung des Dopplereffektes
Bei der Erklärung des akustischen Dopplereffekts ist zu unterscheiden, ob sich die Schallquelle, der Beobachter, oder beide relativ zum Medium (der ruhenden Luft) bewegen.
Beobachter in Ruhe, Signalquelle bewegt
Als Beispiel soll angenommen werden, dass das Martinshorn des Krankenwagens Schallwellen mit einer Frequenz von 1000 Hertz aussendet. Dies bedeutet, dass genau 1/1000 Sekunde nach dem ersten Wellenberg ein zweiter Wellenberg nachfolgt. Die Wellen breiten sich mit der Schallgeschwindigkeit
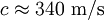 bei 20 °C aus. Solange der Krankenwagen steht, ist der Abstand der Wellenberge (also die Distanz, die der erste Wellenberg zurückgelegt hat, bis der zweite nachfolgt)
bei 20 °C aus. Solange der Krankenwagen steht, ist der Abstand der Wellenberge (also die Distanz, die der erste Wellenberg zurückgelegt hat, bis der zweite nachfolgt) 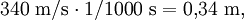 was man als Wellenlänge λ bezeichnet. Für einen Beobachter an der Straße kommen diese Wellenberge zwar je nach Entfernung etwas zeitverzögert an, die Zeit zwischen zwei Wellenbergen ändert sich aber nicht, und damit auch nicht die wahrgenommene Tonhöhe (Frequenz f). Wie man aus obigem Zahlenbeispiel sieht, gibt es einen Zusammenhang zwischen Schallgeschwindigkeit, Wellenlänge und Frequenz, die sich formelmäßig als
was man als Wellenlänge λ bezeichnet. Für einen Beobachter an der Straße kommen diese Wellenberge zwar je nach Entfernung etwas zeitverzögert an, die Zeit zwischen zwei Wellenbergen ändert sich aber nicht, und damit auch nicht die wahrgenommene Tonhöhe (Frequenz f). Wie man aus obigem Zahlenbeispiel sieht, gibt es einen Zusammenhang zwischen Schallgeschwindigkeit, Wellenlänge und Frequenz, die sich formelmäßig als 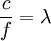 (oder gebräuchlicher äquivalent als
(oder gebräuchlicher äquivalent als 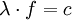 ) darstellen lässt.
) darstellen lässt.Die Situation ändert sich aber, wenn der Krankenwagen auf den Beobachter zufährt. Da sich der Wagen in der Zeit zwischen den beiden Wellenbergen weiterbewegt, verkürzt sich der Abstand zwischen ihnen (also die Wellenlänge) etwas, nämlich genau um den Weg, den der Wagen in der Zeit von 1/1000 Sekunde zurücklegt
(formelmäßig: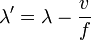 , wenn v die Geschwindigkeit des Wagens ist). Da sich beide Wellenberge mit derselben (Schall-)geschwindigkeit zum Beobachter bewegen, bleibt der verkürzte Abstand zwischen ihnen erhalten, und der zweite Wellenberg kommt nicht erst 1/1000 Sekunde nach dem ersten an, sondern schon ein wenig früher. Dadurch erscheint dem Beobachter die Frequenz (also die Tonhöhe) des Martinshornes höher.
, wenn v die Geschwindigkeit des Wagens ist). Da sich beide Wellenberge mit derselben (Schall-)geschwindigkeit zum Beobachter bewegen, bleibt der verkürzte Abstand zwischen ihnen erhalten, und der zweite Wellenberg kommt nicht erst 1/1000 Sekunde nach dem ersten an, sondern schon ein wenig früher. Dadurch erscheint dem Beobachter die Frequenz (also die Tonhöhe) des Martinshornes höher.Quantitativ erhält man die Frequenzänderung einfach durch Einsetzen der Beziehung
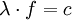 in obige Formel für λ'. Für die vom Beobachter wahrgenommene Frequenz f' ergibt sich so:
in obige Formel für λ'. Für die vom Beobachter wahrgenommene Frequenz f' ergibt sich so:- (1)
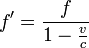
Dabei bedeuten f die Frequenz der Schallquelle, c die Ausbreitungsgeschwindigkeit des Schalls und v die Geschwindigkeit der Schallquelle (also des Krankenwagens).
Wenn der Krankenwagen am Beobachter vorbei gefahren ist, verhält es sich sinngemäß umgekehrt: der Abstand zwischen den Wellenbergen (Wellenlänge) vergrößert sich, und der Beobachter hört einen tieferen Ton. Rechnerisch gilt obige Formel genauso, man muss nur für v eine negative Geschwindigkeit einsetzen.
Beobachter bewegt, Signalquelle in Ruhe
Auch bei ruhender Schallquelle und bewegtem Beobachter tritt ein Dopplereffekt auf, allerdings ist hier die Ursache eine andere: wenn der Wagen ruht, ändert sich auch nichts am Abstand zwischen den Wellenbergen, die Wellenlänge bleibt also gleich. Allerdings kommen die Wellenberge schneller hintereinander bei dem Beobachter an, wenn sich dieser auf den Krankenwagen zubewegt: Da sie sich ihm mit der addierten Geschwindigkeit c + v statt nur mit c nähern, nimmt der zeitliche Abstand zwischen ihnen im Verhältnis dieser Geschwindigkeiten ab
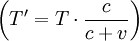 , und die Frequenz, die einfach der Kehrwert dieser Zeit ist, dementsprechend zu. Wenn man noch durchkürzt, ergibt sich:
, und die Frequenz, die einfach der Kehrwert dieser Zeit ist, dementsprechend zu. Wenn man noch durchkürzt, ergibt sich:- (2)
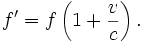
Auch hier wieder ergibt sich der Fall eines sich entfernenden Beobachters durch Einsetzen einer negativen Geschwindigkeit.
Wie man sieht, sind die Gleichungen (1) und (2) nicht identisch (nur im Grenzfall
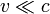 nähern sie sich einander an). Offensichtlich wird das im Extremfall: bewegt sich der Beobachter mit Schallgeschwindigkeit auf die Signalquelle zu, erreichen ihn die Wellenberge doppelt so schnell, und er hört einen Ton doppelter Frequenz. Bewegt sich hingegen die Signalquelle mit Schallgeschwindigkeit, wird der Abstand zwischen den Wellenbergen praktisch null, sie überlagern sich und es kommt zu einer extremen Verdichtung der Luft (siehe Schallmauerdurchbruch). Da so alle Wellenberge gleichzeitig beim Beobachter eintreffen, wäre das nach obiger Formel theoretisch eine unendliche Frequenz - praktisch hört man keinen Ton einer bestimmten Frequenz, sondern den Überschallknall.
nähern sie sich einander an). Offensichtlich wird das im Extremfall: bewegt sich der Beobachter mit Schallgeschwindigkeit auf die Signalquelle zu, erreichen ihn die Wellenberge doppelt so schnell, und er hört einen Ton doppelter Frequenz. Bewegt sich hingegen die Signalquelle mit Schallgeschwindigkeit, wird der Abstand zwischen den Wellenbergen praktisch null, sie überlagern sich und es kommt zu einer extremen Verdichtung der Luft (siehe Schallmauerdurchbruch). Da so alle Wellenberge gleichzeitig beim Beobachter eintreffen, wäre das nach obiger Formel theoretisch eine unendliche Frequenz - praktisch hört man keinen Ton einer bestimmten Frequenz, sondern den Überschallknall.Beobachter und Signalquelle bewegt
Durch Kombination der Gleichungen (1) und (2) kann man eine Gleichung herleiten, die die für den Beobachter wahrgenommene Frequenz f' beschreibt, wenn der Sender und der Empfänger in Bewegung sind.
Sender und Empfänger bewegen sich aufeinander zu:
- (3)
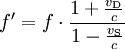
Sender und Empfänger bewegen sich voneinander weg:
- (4)
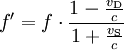
Dabei ist vD die Geschwindigkeit des Empfängers (Detektor) und vS die Geschwindigkeit des Senders der Schallwellen.
Allgemeines Dopplergesetz für Schallquellen
Allgemein lässt sich der Frequenzunterschied schreiben als:
- (5)
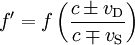
Dabei ist vD die Geschwindigkeit des Empfängers (Detektor) und vS die des Senders der Schallwellen, jeweils relativ zum Medium (z. B. der Luft). Das obere Operationszeichen gilt jeweils für Annäherung (Bewegung in Richtung des Senders bzw. Empfängers). Mit vD = 0 oder vS = 0 ergeben sich die oben genannten Spezialfälle. Weiter sieht man, dass sich der Effekt aufhebt (es also keine Tonhöhenänderung gibt), wenn vS = − vD. Dies entspricht dem Fall, wenn sich Sender und Empfänger beide in dieselbe Richtung mit derselben Geschwindigkeit relativ zum Medium bewegen. Üblicherweise tritt so ein Fall auf, wenn sich das Medium selbst bewegt, während Sender und Empfänger ruhen (Wind). Deswegen kommt es unabhängig von der Windstärke zu keinem Dopplereffekt.
Zu den Formeln ist noch zu sagen, dass sie unter der Annahme abgeleitet wurden, dass sich Quelle und Beobachter direkt aufeinander zubewegen. In realen Fällen fährt der Krankenwagen in einem bestimmten Mindestabstand an dem Beobachter vorbei. Das hat zur Folge, dass sich der Abstand zwischen Quelle und Beobachter nicht gleichmäßig ändert, und deswegen - besonders unmittelbar vor und nach dem Vorbeifahren - ein kontinuierlicher Übergang der Tonhöhe von höher zu tiefer zu hören ist.
Relativistischer Dopplereffekt
Longitudinaler Dopplereffekt
Bei elektromagnetischen Wellen im Vakuum (Optischer Dopplereffekt) gibt es kein Medium, deswegen hängt die beobachtete Frequenzänderung nur von der relativen Geschwindigkeit von Quelle und Beobachter ab; ob sich dabei die Quelle, der Beobachter oder beide bewegen, hat keinen Einfluss auf die Höhe der Frequenzänderung.
Aufgrund des Relativitätsprinzips darf sich jeder Beobachter als ruhend betrachten. Allerdings muss er dann bei der Berechnung des Dopplereffekts zusätzlich zu obigen Betrachtungen auch noch die Zeitdilatation der relativ zum Beobachter bewegten Quelle berücksichtigen. Somit erhält man für den relativistischen Dopplereffekt:
- (6)
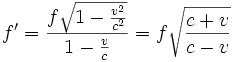 (Quelle und Beobachter nähern sich einander)
(Quelle und Beobachter nähern sich einander)
- (7)
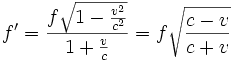 (Quelle und Beobachter entfernen sich voneinander)
(Quelle und Beobachter entfernen sich voneinander)
Bewegt sich die Lichtquelle durch ein Medium mit einer Brechzahl n > 1 (z.B. durch Wasser), so ist in diesem Medium die Lichtgeschwindigkeit c' kleiner als die Vakuum-Lichtgeschwindigkeit. In die Zeitdilatation geht aber weiterhin die Vakuumlichtgeschwindigkeit ein, so dass sich in diesem Fall ergibt:
- (8)
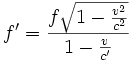
Diese Formel geht für
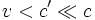 in die nichtrelativistische Formel über, selbst wenn v nicht wesentlich kleiner als c' ist.
in die nichtrelativistische Formel über, selbst wenn v nicht wesentlich kleiner als c' ist.Transversaler Dopplereffekt
Bewegt sich ein Objekt zu einem gewissen Zeitpunkt quer zum Beobachter, so kann man die Änderung des Abstandes zu diesem Zeitpunkt vernachlässigen; dementsprechend würde man hier auch keinen Dopplereffekt erwarten. Jedoch besagt die Relativitätstheorie, dass jedes Objekt aufgrund seiner Bewegung einer Zeitdilatation unterliegt, aufgrund der die Frequenz ebenfalls verringert wird. Diesen Effekt bezeichnet man als transversalen Dopplereffekt. Die Formel hierfür lautet
- (9)
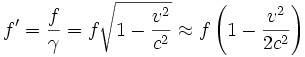
wobei c hier die Vakuum-Lichtgeschwindigkeit bezeichnet.
Der transversale Dopplereffekt kann bei nicht-relativistischen Geschwindigkeiten (also Geschwindigkeiten weit unter der Lichtgeschwindigkeit) allerdings vernachlässigt werden.
Dopplereffekt bei beliebigem Winkel
Der Dopplereffekt lässt sich ganz allgemein abhängig vom Winkel der Bewegungsrichtung zur Achse Quelle-Empfänger angeben. Die Frequenzänderung für beliebige Winkel α ergibt sich zu
- (10)
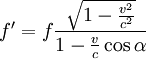 .
.
Wenn man für den Winkel α 0°, 90°, oder 180° einsetzt, dann erhält man die oben stehenden Gleichungen für longitudinalen und transversalen Dopplereffekt. Man erkennt außerdem, dass der Winkel, unter dem der Dopplereffekt verschwindet, von der Relativgeschwindigkeit abhängt, anders als beim Dopplereffekt für Schall, wo er immer 90° beträgt.
Anwendungen
Der Dopplereffekt tritt bei Echos von ausgesendeten akustischen und elektromagnetischen Signalen auf. Beim Doppler-Radar berechnet man die Annäherungsgeschwindigkeit eines Objekts aus der gemessenen Frequenzänderung. In der Medizin wird der akustische Dopplereffekt bei Ultraschalluntersuchungen ausgenutzt, um die Blutstromgeschwindigkeit darzustellen und zu messen. Dabei hat er sich als außerordentlich hilfreich erwiesen. Es gibt dabei einen:
- Farbdoppler:
- Rot: Fluss auf die Schallsonde zu
- Blau: Fluss von der Schallsonde weg
- pW-Doppler: gepulster Doppler (beispielsweise für Gefäßuntersuchungen)
- cW-Doppler: continuous wave Doppler (beispielsweise für Herzklappenmessungen)
In der Meteorologie wird das Dopplerradar zur Bestimmung von Rotationsbewegungen in Superzellen (Tornados) benutzt.
Das Militär und die Flugüberwachung nutzen den Dopplereffekt unter anderem beim Passiv-Radar und bei der Festzielunterdrückung.
Für Wasserwellen (Schwerewellen), deren Trägermedium einer konstanten Strömungsgeschwindigkeit unterliegt, siehe unter Wellentransformation.
Für die berührungslose Messung der Geschwindigkeitsverteilung von Fluiden (Flüssigkeiten und Gase) wird die Laserdoppler-Anemometrie (LDA) angewandt. Eine andere Anwendung, die Laserdoppler-Vibrometrie (LDV), betrifft die Messung der Schwingschnelle von Oberflächen. Hier wird die durch die Oberflächenbewegung hervorgerufene Frequenzverschiebung eines am Messpunkt reflektierten Laserstrahls zur Bestimmung der Schwingschnelle an diesem Messpunkt herangezogen.
Zur Geschwindigkeitsermittlung bei sog. Radarfallen im Straßenverkehr wird ein Dopplerradar benutzt.
Das mittlerweile abgeschaltete Satellitennavigations-System Transit nutzte den Dopplereffekt zur Positionsbestimmung. Aktiv eingesetzt wird er bei Argos, einem satellitengestützten System zur Positionsbestimmung. Bei modernen GNSS-Satelliten ist der Dopplereffekt zunächst störend. Er zwingt die Empfänger, einen größeren Frequenzbereich abzusuchen. Andererseits lassen sich aus der Frequenzverschiebung Zusatzinformationen gewinnen und so die Grobpositionierung beschleunigen. Das Verfahren heißt Doppler-Aiding. Siehe auch: Dopplersatellit.
Dopplerverschiebungen führen im Mobilfunk zu Pegeleinbrüchen, welche in dem Begriff Fast-Fading zusammengefasst sind.
Ein Synthetic Aperture Radar basiert maßgeblich auf der Zuordnung der Signale durch ihre Dopplerverschiebung.
In der Musik wird der Dopplereffekt zur Erzeugung von Klangeffekten verwendet, beispielsweise bei den rotierenden Lautsprechern eines Leslie-Kabinetts.
Bei der Mößbauer-Spektroskopie wird der Doppler-Effekt einer bewegten Gammastrahlungsquelle verwendet, um die Energie der Photonen dieser Quelle minimal zu verändern. Hierdurch können diese Photonen in Wechselwirkung mit den Kernhyperfeinniveaus eines entsprechenden Absorbers treten.
Beispiel
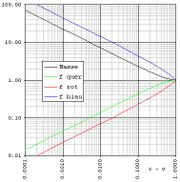
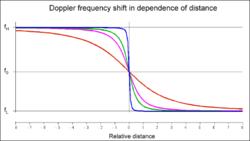
Ein ruhender Beobachter hört eine Schallquelle, die sich genau auf ihn zu bewegt, mit der Frequenz f´zu(v/c), siehe Gleichung (1), wenn sie sich von ihm entfernt, mit der Frequenz f´weg(v/c), siehe Gleichung (2). Bei Schallquellen spielt der relativistische transversale Dopplereffekt keine Rolle. Je weiter der Beobachter von der linearen Flugbahn entfernt ist, desto langsamer ändert sich die radiale Geschwindigkeitskomponente bei Annäherung. Die Schnelligkeit der Frequenzänderung hängt ab von der kürzesten Entfernung zwischen Beobachter und Signalquelle. Das Diagramm rechts zeigt die Frequenzabhängigkeit relativ zu einem im Ursprung ruhenden Beobachter. Die rote Linie entspricht der Frequenz, die er hört, wenn ihn die Signalquelle in großem Abstand passiert, blau der bei geringem Abstand. Maximal- und Minimal-Frequenzen liegen nicht symmetrisch zur Eigenfrequenz, da die Geschwindigkeit v nicht sehr viel kleiner ist als die Schallgeschwindigkeit c. Es gelten die Beziehungen (1) und (2).
Sind die Koordinaten der bewegten Signalquelle bekannt, kann man aus dem Frequenzverlauf den eigenen Standort ableiten (siehe z.B. Transit (Satellitensystem)).
Die Tonbeispiele geben die Tonhöhen, die ein ruhender Beobachter hört, wenn eine Signalquelle an ihm vorbeifliegt. Sie vernachlässigen den Effekt, dass die sich entfernende Quelle länger zu hören ist als die sich nähernde:
- Frequenz f0 = 400 Hz, relative Geschwindigkeit v/c = 0,1 (dann ist fzu_max = 440 Hz und fweg_min = 360 Hz):
- (1)
 Doppler-Beispiel 1?/i Langsam bewegte Signalquelle, die Beobachter in geringem Abstand passiert.
Doppler-Beispiel 1?/i Langsam bewegte Signalquelle, die Beobachter in geringem Abstand passiert. - (2)
 Doppler-Beispiel 2?/i: wie (1), aber Passieren der Signalquelle in größerem Abstand.
Doppler-Beispiel 2?/i: wie (1), aber Passieren der Signalquelle in größerem Abstand. - (3)
 Doppler-Beispiel 3?/i: wie (2), Abstand noch größer.
Doppler-Beispiel 3?/i: wie (2), Abstand noch größer.
Erhöht sich die relative Geschwindigkeit, verschieben sich die Frequenzen:
- Frequenz wie oben, aber v/c = 0,42 (dann ist fzu_max = 690 Hz, fweg_min = 280 Hz).
- (4)
 Doppler-Beispiel 2b?/i: Abstand wie (2).
Doppler-Beispiel 2b?/i: Abstand wie (2).
Siehe auch
- Dopplerverbreiterung
- Rotverschiebung in der Astronomie
Weblinks
- Facharbeiten zum Dopplereffekt von B. Fries und H. Richter (PDF)
- Vorlesungen der Universität Tübingen zum Doppler-Effekt
- Beispiele für verschiedene Geschwindigkeiten eines Objekts
- (1)
Wikimedia Foundation.