Wilcoxon signed-rank Test

Der Wilcoxon-Vorzeichen-Rang-Test ist ein statistischer Test für die Häufigkeitsverteilung gepaarter Stichproben. Im Anwendungsbereich ergänzt er den Vorzeichentest, da er nicht nur die Richtung der Differenzen, sondern auch die Stärke der Differenzen zwischen zwei gepaarten Stichproben berücksichtigt. Der hier vorgestellte Test ist unabhängig vom Verteilungstyp und wird daher als nichtparametrisch bezeichnet.

Dieser statistische Test wurde vom Chemiker und Statistiker Frank Wilcoxon (1892–1965) vorgeschlagen und durch das Lehrbuch von Sidney Siegel – Nonparametric Statistics for the Behavioural Sciences – populär gemacht.

Beispiel

Ein Beispiel für dessen Anwendung: Ein statistisch versierter Bauer möchte feststellen, ob Rinder Heu oder Stroh vorziehen. Er teilt eine Fläche in zwei Bereiche ein, zwischen denen die Tiere frei hin und her wechseln können. Im einen Bereich bietet er den fünf Rindern Stroh an, im anderen Heu. Jede halbe Stunde notiert er, wieviele Tiere sich in welchem Bereich aufhalten; er erhält N = 6 Paare von Stichproben.

Das Ergebnis seiner Beobachtungen ist eine Tabelle, und er berechnet auch die Differenzen aus den Werten:

Tiere beim Heu	Tiere beim Stroh	Differenz
4	1	+3
3	2	+1
2	3	-1
5	0	+5
5	0	+5
3	2	+1

Dann werden die Differenzen nach der Größe geordnet (das Vorzeichen wird dabei nicht berücksichtigt); und jeder Differenz wird ein Rang zugeordnet – die größte Differenz erhält den höchsten Rang. Sind mehrere Differenzen gleichrangig, wird jedem Wert der durchschnittliche Rang zugeordnet.

Differenz	Rang
+1	2
+1	2
-1	2
+3	4
+5	5.5
+5	5.5

Rang: Die drei 1er Werte müssten die Ränge 1 bis 3 belegen, da sie aber gleichwertig sind, wird der Mittelwert ihrer Ränge eingetragen, also (1+2+3)/3=2. Bei den 5er Werten ebenso: (5+6)/2=5.5

Die Rangsumme der positiven Differenzen beträgt

T⁺ = 2+2+4+5.5+5.5 = 19

Entweder verfügt man über eine Tabelle über diese T⁺- und N-Werte und kann so die Wahrscheinlichkeit einer solchen Beobachtung direkt bestimmen, oder man berechnet – als Näherung – daraus den normalverteilten z-Wert:

$z = \frac{T-\frac{N(N+1)}{4}}{\sqrt{\frac{N(N+1)(2N+1)}{24}}}$

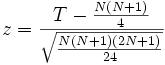
z	Signifikanz
> 1.65 oder < -1.65	signifikant mit p = 0.1
> 1.96 oder < -1.96	signifikant mit p = 0.05
> 2.58 oder < -2.58	signifikant mit p = 0.01
> 2.81 oder < -2.81	signifikant mit p = 0.005
> 3.29 oder < -3.29	signifikant mit p = 0.001

p mit 100 multipliziert gibt jeweils den Wert der Irrtumswahrscheinlichkeit – das heißt, die Wahrscheinlichkeit, dass eine Beobachtung durch zufällige Effekte zustande gekommen ist. Weitere Werte für z sind in der Standardnormalverteilungstabelle aufgelistet.

In diesem Beispiel ist z = 1.7821. Die Beobachtungen des Bauers sind also mit p < 0.1 und p > 0.05 vielleicht signifikant. Damit haben Rinder zu einem 10%-Signifikanzniveau eine Vorliebe für Heu. Der mittels der angegebenen Formel berechnete z-Wert ist aber nur eine Näherung und nur für einen großen Stichprobenumfang zuverlässig. Das Tabellenwerk aus dem Buch von Sidney Siegel enthält p-Werte für bis zu N = 15 Stichproben.

Vergleich mit dem Vorzeichentest

Fünf Stichproben tragen ein positives Vorzeichen (+), eine ein negatives (-). Gemäß der Tabelle der kritischen Werte (MacKinnon, 1964) kann man bei diesem Beispiel lediglich von p < 0.5 ausgehen (d.h. weniger als 50 Prozent Irrtumswahrscheinlichkeit). Hätten alle sechs Stichproben das gleiche Vorzeichen, läge p zwischen 0.02 und 0.1 - hier wurde also eindrücklich gezeigt, dass das Verfahren von Wilcoxon besonders bei kleineren Stichproben-Umfängen brauchbare Resultate liefert.

Literatur

• Siegel, Sidney. - Nichtparametrische statistische Methoden - Eschborn b. Frankfurt a. M. : Verlag Dietmar Klotz, 2001. ISBN 3-88074-102-6.
• Siegel, Sidney. - Nonparametric statistics for the behavioral sciences - New York [etc.] : McGraw-Hill, c. 1988 (vergriffen)