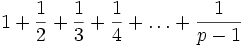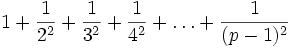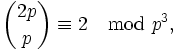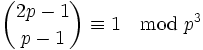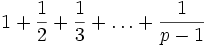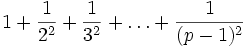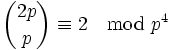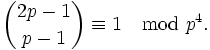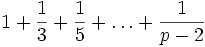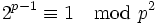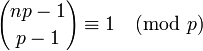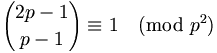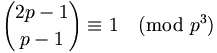Wolstenholme-Primzahl

Der Satz von Wolstenholme (nach Joseph Wolstenholme) ist eine Aussage aus dem mathematischen Teilgebiet der Zahlentheorie. In einer möglichen Form besagt er: Ist 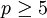$p\geq5$ eine Primzahl, so ist der Zähler der rationalen Zahl

$1+\frac12+\frac13+\frac14+\ldots+\frac1{p-1}$

durch p² teilbar.^[1]

Andere Formulierungen, Folgerungen

Der Satz ist äquivalent zu der Aussage, dass der Zähler von

$1+\frac1{2^2}+\frac1{3^2}+\frac1{4^2}+\ldots+\frac1{(p-1)^2}$

durch p teilbar ist.^[2]

Eine Folgerung aus dem Satz ist die Kongruenz

${2p\choose p}\equiv2\mod{p^3},$

die auch in der Form

${2p-1\choose p-1}\equiv1\mod{p^3}$

geschrieben werden kann.

Wolstenholme-Primzahlen

Eine Wolstenholme-Primzahl p ist eine Primzahl, die eine stärkere Fassung des Satzes von Wolstenholme erfüllt, genauer: die eine der folgenden äquivalenten Bedingungen erfüllt:^[3]

• Der Zähler von

$1+\frac12+\frac13+\dots+\frac1{p-1}$

ist durch p³ teilbar.

• Der Zähler von

$1+\frac1{2^2}+\frac1{3^2}+\dots+\frac1{(p-1)^2}$

ist durch p² teilbar.

• Es gilt die Kongruenz

${2p\choose p}\equiv2\mod{p^4}$

bzw. die Kongruenz

${2p-1\choose p-1}\equiv1\mod{p^4}.$

• Der Zähler der Bernoulli-Zahl B_{p − 3} ist durch p teilbar.

Die beiden bisher einzigen bekannten Wolstenholme-Primzahlen sind 16843 und 2124679. Jede weitere Wolstenholme-Primzahl müsste größer als 6,4·10⁸ sein.

Verwandter Begriff

Betrachtet man nur ungerade Nenner, also die Summe

$1+\frac13+\frac15+\dots+\frac1{p-2}$

für eine Primzahl 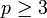$p\geq3$, so ist der Zähler genau dann durch p teilbar, wenn die stärkere Form

$2^{p-1}\equiv1\mod{p^2}$

des Satzes von Euler-Fermat gilt.^[4] Derartige Primzahlen heißen Wieferich-Primzahlen.

Geschichte

Aus dem Satz von Wilson (p ist genau dann eine Primzahl, wenn 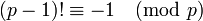$(p-1)! \equiv -1 \pmod p$ ist) folgt, dass für jede Primzahl p und jede natürliche Zahl n die Kongruenz

${{np-1}\choose{p-1}} \equiv 1 \pmod{p}$

erfüllt ist.

Charles Babbage bewies 1819, dass für jede Primzahl p>2 diese Kongruenz gilt:

${{2p-1}\choose{p-1}} \equiv 1 \pmod{p^2}$

Der Mathematiker Joseph Wolstenholme (1829-1891) bewies dann 1862, dass für jede Primzahl p>3 die folgende Kongruenz gilt:

${{2p-1}\choose{p-1}} \equiv 1 \pmod{p^3}$

Literatur

• G. H. Hardy, E. M. Wright, An Introduction to the Theory of Numbers, 4. Auflage, Oxford University Press, Oxford 1975. ISBN 0-19-853310-1
• J. Wolstenholme, On certain properties of prime numbers, Quart. J. Math. Oxford Ser. 5 (1862) 35–39

Quellen

1. ↑ Hardy-Wright, a.a.O., Theorem 115, S. 88
2. ↑ Hardy-Wright, a.a.O., Theorem 117, S. 90
3. ↑ A. Gardiner, Four problems on prime power divisibility. Am. Math. Mon. 95, No. 10 (1988) 926–931
4. ↑ Hardy-Wright, a.a.O., Theorem 132, S. 104

Weblinks

• The Prime Glossary: Wolstenholme prime (englisch)