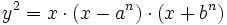Fermats letzter Satz

Pierre de Fermat.

Der große fermatsche Satz wurde im 17. Jahrhundert von Pierre de Fermat formuliert, aber erst 1993 von Wiles und Taylor bewiesen (1995 veröffentlicht). Er besagt, dass die n-te Potenz einer Zahl, wenn n > 2 ist, nicht in die Summe zweier Potenzen des gleichen Grades zerlegt werden kann; gemeint sind ganze Zahlen 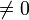$\neq 0$ und natürliche Potenzen. Formaler gesagt bedeutet dies:

Die Gleichung

aⁿ + bⁿ = cⁿ

besitzt für ganzzahlige 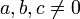$a,b,c \neq 0$ und natürliche Zahlen n > 2 keine Lösung.

Erstaunlich ist dieser Satz, weil es für 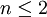$n\leq 2$ unendlich viele Lösungen der Gleichung gibt (für n = 2 sind dies die pythagoreischen Zahlentripel), und weil Fermat sogleich behauptet hatte, er wisse einen Beweis, den er allerdings nicht mitteilte und den weder Mathematiker noch Historiker bisher wiederfinden konnten. Der mehr als 350 Jahre später erbrachte Beweis verwendet Mittel, die Fermat keinesfalls zur Verfügung gestanden hatten.

Bezeichnungen

• Großer fermatscher Satz, daraus abgeleitet großer Fermat im Gegensatz zum kleinen fermatschen Satz bzw. kleinen Fermat
• Fermatsche Vermutung (vor dem mathematischen Beweis handelte es sich fast 400 Jahre lang nur um eine Vermutung, trotzdem wurde schon damals fälschlicherweise von Satz gesprochen)
• Höhere Abwandlungen des Satzes von Pythagoras
• Fermats letzter Satz bzw. Fermats letztes Theorem, abgeleitet aus der (schlechten) wörtlichen Übersetzung des englischen Fermat's Last Theorem

Ursprung

Im Jahr 1637 schrieb Fermat bei der Lektüre der ARITHMETICA von Diophantos neben den Satz des Pythagoras folgende Zeilen als Randbemerkung in seine Ausgabe dieses Buches:

„Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos eiusdem nominis fas est dividere. Cuius rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caperet.“

Auf deutsch:

„Es ist unmöglich, einen Kubus in zwei Kuben zu zerlegen, oder ein Biquadrat in zwei Biquadrate, oder allgemein irgendeine Potenz größer als die zweite in Potenzen gleichen Grades. Ich habe hierfür einen wahrhaft wunderbaren Beweis gefunden, doch ist der Rand hier zu schmal, um ihn zu fassen.“

Verbreitung

Nach dem Tode Fermats drohte sein geistiges Erbe verloren zu gehen, da er ein recht unangenehmer Korrespondenzpartner für seine Mathematikerkollegen gewesen war und auch nie Kontakte zur Pariser Mathematikerschule gepflegt hatte. Sein ältester Sohn Clément-Samuel verbrachte fünf Jahre auf die Entzifferung der Notizen und veröffentlichte anschließend eine eigene Ausgabe der Arithmetica, in der auch achtundvierzig der Bemerkungen seines Vaters angeführt waren. Die zweite dieser Randnotizen wurde dann in weiterer Folge als fermatsche Vermutung bekannt. Die Notizen enthielten zwar eine Reihe von fundamentalen mathematischen Sätzen, aber Beweise dazu oder auch nur einfache Erklärungen, wie Fermat zu diesen Resultaten gekommen war, fehlten völlig. Es war nun den nachfolgenden Mathematikern überlassen, diese aufzustellen.

Unsicherheit

In diesem Kontext entwickelte sich speziell der große fermatsche Satz in den folgenden Jahrhunderten zu einem Albtraum für viele Mathematiker – niemand konnte ihn beweisen oder widerlegen. Weil aber gerade Fermat selbst die Ansicht vertreten hatte, dass er einen wunderbaren Beweis gefunden habe, versuchten sich Generationen von Mathematikern – darunter auch die bedeutendsten ihrer Zeit – an der Findung des Beweises. Ebenso sollten sich auch die anderen Bemerkungen Fermats als schwierige, jahrelange Arbeit für seine Mathematikerkollegen erweisen. Die einzelnen Beweisführungen an sich hatten – sozusagen als Nebenprodukte – eine Vielzahl von fundamentalen Entdeckungen zur Folge.

Beweise für Spezialfälle des Satzes

Für spezielle Fälle des großen fermatschen Satzes konnten Beweise erbracht werden:

n = 3, n = 4 und Vielfache dieser Zahlen

Leonhard Euler entdeckte in der fermatschen Version der Arithmetica einen gut versteckten Beweis für den Fall n = 4. Im Jahr 1753 konnte er (mit Hilfe der imaginären Zahlen) die Behauptung auch für den Fall n = 3 bestätigen. Damit war die fermatsche Vermutung auch für alle n, die ein Vielfaches von 3 oder 4 sind (also 6, 9, 12, ... und 8, 12, 16, ...) bewiesen. Euler gelang es aber nicht, seine Beweismethode auf weitere Einzelfälle auszudehnen.

Primzahlen reichen aus

Bald darauf wurde klar, dass es ausreicht, den fermatschen Satz für alle Primzahlen größer 2 und die Zahl 4 zu beweisen – er lässt sich dann auf alle Vielfachen dieser Zahlen übertragen. Doch auch bei den Primzahlen hatte man es immer noch mit einer unendlichen Zahlenmenge zu tun und damit auch mit unendlich vielen zu beweisenden Fällen.

n = 5 und alle Sophie-Germain-Primzahlen

Im Jahre 1825 konnten Peter Gustav Lejeune-Dirichlet und Adrien-Marie Legendre den Satz für n = 5 beweisen. Sie stützten sich dabei auf die Vorarbeit von Sophie Germain. Germain meinte, dass die fermatsche Vermutung vermutlich für alle Sophie-Germain-Primzahlen gilt. „Vermutlich“ soll heißen, dass wenn es Lösungen gäbe, müssten a, b, oder c Vielfache von n sein; diese Bedingung ist auch als zweiter Fall bekannt. Bis zu den Arbeiten von Wiles und Taylor war jedoch weder für den ersten Fall (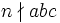$n\nmid abc$) noch für den zweiten Fall (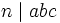$n\mid abc$) ein allgemeiner Beweis bekannt.

n = 7

1839 zeigte Gabriel Lamé, dass auch der Fall n = 7 Gültigkeit besitzt. Ebenso wie Augustin Louis Cauchy war Lamé noch im März 1847 überzeugt, den vollständigen Beweis für die fermatsche Vermutung innerhalb von Wochen der französischen Akademie der Wissenschaften vorlegen zu können.

Alle regulären Primzahlen

Diese Hoffnung wurde aber von Ernst Eduard Kummer zunichte gemacht, der einen grundlegenden Denkfehler beider Mathematiker entdeckte: Sie waren stillschweigend davon ausgegangen, dass in den von ihnen betrachteten Erweiterungen des Körpers der rationalen Zahlen (Kreisteilungskörpern der Ordnung p) für die jeweilige Fermatgleichung zum Exponent p (er entsteht durch Adjunktion der p-ten Einheitswurzeln) noch die eindeutige Primfaktorzerlegung gilt.

Kummer entwickelte eine Theorie, in der sich die eindeutige Primfaktorzerlegung retten ließ, indem man ganze Gruppen von Zahlen des Zahlkörpers (Ideale) zusammenfasst und die Arithmetik dieser neuen „idealen Zahlen“ untersucht. Er konnte damit den großen fermatschen Satz 1846 für reguläre Primzahlen beweisen; dabei heißt eine Primzahl p regulär, wenn keine der Bernoulli-Zahlen 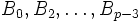$B_0,B_2,\ldots,B_{p-3}$ durch p teilbar ist. In diesem Fall ist die Klassenzahl (Anzahl der nicht äquivalenten Idealklassen) des Kreisteilungskörpers der Ordnung p durch p teilbar. Es ist nicht bekannt, ob es unendlich viele reguläre Primzahlen gibt.

Mit Hilfe des Computers und mit Weiterentwicklung der Methoden von Kummer gelang es Harry Vandiver schon Anfang der 1950er Jahre, den Satz für alle Primzahlen kleiner als 2000 zu beweisen. Die Grenze konnte mit Hilfe des Computers noch erheblich nach oben verschoben werden, einer Lösung der Vermutung kam man aber auf diesem Weg nicht näher, sie wurde nur plausibler.

Neuer Ansporn

Die Suche nach einem allgemeinen Beweis wurde zu Beginn des 20. Jahrhunderts durch das Testament des Darmstädter Mathematikers Paul Friedrich Wolfskehl auch materiell motiviert. Einer später erzählten Legende zufolge ist dessen Schicksal auf sehr seltsame Weise mit dem fermatschen Satz verbunden. Als seine Liebe zu einer Frau von dieser nicht erwidert wurde, fasste er den Entschluss sich selbst zu töten. Er setzte den Zeitpunkt seines Freitodes genau auf Mitternacht fest und wollte sich bis dorthin die Zeit vertreiben. Aus Zufall stolperte er über eine Arbeit über die fermatsche Behauptung und war von dieser derart gefesselt, dass er über ihr die Zeit vergaß. Wolfskehl überlebte aus diesem Grund diese Nacht, ließ von seinen Selbstmordgedanken ab und änderte aus Dank sein Testament.

Als er dann 1906 tatsächlich starb, hatte er darin festgelegt, dass er 100.000 Goldmark für denjenigen aussetzte, der zuerst einen vollständigen Beweis in einer Fachzeitschrift veröffentliche. Daraufhin wurde 1908 von der Königlichen Gesellschaft der Wissenschaften zu Göttingen der Wolfskehl-Preis ausgeschrieben. Der Einsendeschluss für dieses Unterfangen sollte der 23. September 2007 sein. Durch die Hyperinflation nach dem Ersten Weltkrieg wurde der Geldpreis aber stark entwertet. Im Jahr 1997 wurde der Preis (der noch umgerechnet 70.000 DM wert war) an Andrew Wiles ausbezahlt.

Fermats Beweis nur für den Spezialfall

Heute wird angenommen, dass Fermat einen Beweis für einen Spezialfall (n = 4) gefunden hatte, von dem er glaubte, ihn verallgemeinern zu können. Die von Wiles benutzten Theorien waren vor über dreihundert Jahren längst noch nicht entwickelt. Deshalb ist es heute unter Zahlentheoretikern strittig, ob es nicht doch einen elementareren Beweis gibt, den Fermat eventuell entdeckt haben könnte.

Der Beweis

1994 gelang es dem britischen Mathematiker Andrew Wiles zusammen mit seinem Schüler Richard Taylor, die fermatsche Vermutung zu beweisen (Lit.: Wiles, 1995). Der eigentliche Beweis besteht aus zwei Teilen:

• Sind a,b,c,n mit aⁿ + bⁿ = cⁿ ein Gegenbeispiel für den fermatschen Satz, so ist die elliptische Kurve

$y^2 = x \cdot (x - a^n) \cdot (x + b^n)$

nicht modular. Dies wurde 1986 von Gerhard Frey vermutet und über einen Beitrag von Jean-Pierre Serre 1990 durch Ken Ribet bewiesen.

• Alle elliptischen Kurven sind modular. Diese so genannte Taniyama-Shimura-Vermutung (nach Taniyama und Shimura, manchmal auch nach A. Weil benannt) wurde für eine große Klasse von elliptischen Kurven, die die Frey-Kurve umfasst, 1994 von A. Wiles und R. Taylor bewiesen.

Im 98-seitigen Beweis (ohne Appendix und Literaturverzeichnis) (Lit.: Wiles, 1995) nutzt Wiles viele Konstruktionen aus dem umfangreichen Gebäude der modernen Zahlentheorie. Aufgrund der langen Geschichte des Beweises und auch, weil Wiles völlig neue Zusammenhänge in der Zahlentheorie und zwischen Teilgebieten der Mathematik erschloss, gilt seine Arbeit unter Mathematikern als eine der bedeutendsten des 20. Jahrhunderts. Das Bemerkenswerteste an diesem Beweis ist wohl die Tatsache, dass ihn nur ein sehr geringer Anteil der Zahlentheoretiker vollständig versteht. Er ist ein Stück modernster algebraischer Zahlentheorie.

Siehe auch

• Kleiner fermatscher Satz
• Catalansche Vermutung
• Wall-Sun-Sun-Primzahl
• Wieferich-Primzahl
• Wolstenholme-Primzahl

Literatur

Originalarbeiten

• Andrew Wiles: Modular Elliptic Curves and Fermat's last theorem. Annals of Mathematics 142 (1995), 443–551
• Richard Taylor, Andrew Wiles: Ring-theoretic properties of certain Hecke algebras. Annals of Mathematics 142 (1995), 553–572.
• Kenneth A. Ribet: On modular representations of 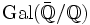$\mathrm{Gal}(\bar{\mathbb Q}/\mathbb Q)$ arising from modular forms. Inventiones Mathematicae 100 (1990), 431–476
• G. Frey: Links between stable elliptic curves and certain diophantine equations. Annales Universitatis Saraviensis. Series Mathematicae 1 (1986), 1–40

Übersichtsartikel und Historisches

• Paulo Ribenboim: 13 lectures on Fermat's last theorem, Springer, New York, 1979 (die wichtigsten Arbeiten vor Wiles)
• Paulo Ribenboim : Fermats last theorem for Amateurs, Springer 2000, ISBN 0-387-98508-5
• Simon Singh: Fermats letzter Satz – Die abenteuerliche Geschichte eines mathematischen Rätsels. ISBN 3-423-33052-X
• Die Königliche Gesellschaft der Wissenschaften: Bekanntmachung betr. die Wolfskehlsche Preisstiftung. Nachrichten von der Königlichen Gesellschaft der Wissenschaften zu Göttingen. Geschäftliche Mitteilungen 16:1 (1908), 103–104.
• Simon Singh und Kenneth Ribet: Die Lösung des Fermatschen Rätsels, Spektrum der Wissenschaft 1/98, Seite 96 ff. ISSN 0170-2971
• Kenneth A. Ribet: Galois Representations and Modular Forms, Bulletin of the AMS 32 (4/1995), 375–402
• Gerd Faltings: The Proof of Fermat's last theorem by R. Taylor and A. Wiles, Notices of the AMS 42 (7/1995), 743–746.
• Peter Roquette, Zum Fermat-Problem. Vortrag am Mathematischen Institut der Universität Heidelberg, 24. Januar 1998.
• Joseph Silverman, Gary Connell, Glen Stevens (Herausgeber): Modular Forms and Fermat's Last Theorem, Springer-Verlag 1997 (mathematisches Hintergrundmaterial zu und Darstellung von Wiles Beweis)