- Wurzel-Kriterium
-
Das Wurzelkriterium ist ein mathematisches Konvergenzkriterium, also ein Mittel zur Entscheidung, ob eine unendliche Reihe konvergent oder divergent ist.
Inhaltsverzeichnis
Formulierungen
Sei eine unendliche Reihe
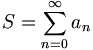 mit reellen oder komplexen Summanden an gegeben. Falls man nun
mit reellen oder komplexen Summanden an gegeben. Falls man nun![\limsup_{n\to\infty}\sqrt[n]{|a_{n}|}<1](/pictures/dewiki/48/038a1d7425ffb84b0d7471a7375e30ed.png) oder
oder![\sqrt[n]{|a_{n}|}\le C](/pictures/dewiki/51/36fe0caf3f7559aa2df316ca53dc7e24.png) für ein C<1 und fast alle Indizes n
für ein C<1 und fast alle Indizes n
nachweisen kann, so konvergiert die Reihe S, und das sogar absolut. Ist jedoch
![\limsup_{n\to\infty}\sqrt[n]{|a_{n}|}&gt; 1](/pictures/dewiki/100/d62e902004c7decacf1b6916d6ef33ba.png) oder
oder![\sqrt[n]{|a_n|} \ge 1](/pictures/dewiki/55/705bd861d174c96ad957d6a065e0c534.png) für unendlich viele Indizes n,
für unendlich viele Indizes n,
so divergiert die Reihe, da die Reihenglieder keine Nullfolge bilden. Im Fall
![\limsup_{n\to\infty}\sqrt[n]{|a_{n}|}= 1](/pictures/dewiki/97/aa0ca0ed560a7cded05400757768713b.png) und
und![\sqrt[n]{|a_n|} &lt; 1](/pictures/dewiki/54/636aa49992846f8cd0df9857b11af92c.png) für fast alle Indizes n
für fast alle Indizes n
lässt sich nichts über die Konvergenz der Reihe aussagen. So lässt sich beispielsweise mit dem Wurzelkriterium keine Aussage über die Konvergenz der allgemeinen harmonischen Reihe
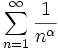 für
für 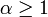 machen, da
machen, da![\limsup_{n\to\infty}\sqrt[n]{|a_n|}=\lim_{n\to\infty}\sqrt[n]{1/n^\alpha}=\left(\lim_{n\to\infty}\sqrt[n]{1/n}\right)^\alpha= 1](/pictures/dewiki/98/b491efbc2c69caa3da83d3d20a94a512.png) .
.
Für α = 1 ist die allgemeine harmonische Reihe divergent, für α > 1 konvergent; das Wurzelkriterium kann aber die beiden Fälle nicht unterscheiden.
Beweisskizze
Das Wurzelkriterium wurde erstmals von Augustin Louis Cauchy bewiesen. Es folgt mit dem Majorantenkriterium aus Eigenschaften der geometrischen Reihe:
- Denn gilt für alle
![n\in\mathbb N:\;\sqrt[n]{|a_{n}|}\le C&lt;1](/pictures/dewiki/98/b136073ee2e4385f018948476a375c39.png) , so ist das Majorantenkriterium
, so ist das Majorantenkriterium 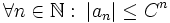 mit einer konvergenten geometrischen Reihe
mit einer konvergenten geometrischen Reihe 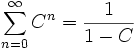 als Majorante erfüllt.
als Majorante erfüllt.
- Daran ändert sich auch nichts, falls dieses Kriterium für die ersten N Glieder der Reihe nicht
erfüllt ist.
- Gilt
![\limsup_{n\to\infty}\sqrt[n]{|a_{n}|}=C&lt;1](/pictures/dewiki/55/793caf61597dd2e7fbd209569413dd72.png) , so ist
, so ist ![\sqrt[n]{|a_{n}|}\le \frac{1+C}2&lt;1](/pictures/dewiki/100/d1d9fee2324e79aab03b5e210edbbbcc.png) für fast alle n erfüllt, nach Definition des größten Häufungspunktes, womit wieder eine Majorante konstruiert werden kann.
für fast alle n erfüllt, nach Definition des größten Häufungspunktes, womit wieder eine Majorante konstruiert werden kann.
Restgliedabschätzung
Ist die Reihe nach dem Wurzelkriterium konvergent, erhält man noch eine Fehlerabschätzung, d.h. eine Abschätzung des Restglieds der Summe nach N Summanden:
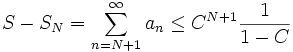 .
.
Das Wurzelkriterium ist schärfer als das Quotientenkriterium
Sei
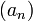 eine positive Folge und sei
eine positive Folge und sei![\alpha=\liminf \frac{a_{n+1}}{a_n} \quad , \quad \alpha'=\liminf \sqrt[n]{a_n} \quad , \quad
\beta'=\limsup \sqrt[n]{a_n} \quad , \quad \beta=\limsup \frac{a_{n+1}}{a_n}](/pictures/dewiki/55/70120c44e72c43e0b86ab4a815262f27.png) .
.
Liefert bei einer Reihe das
Quotientenkriterium eine Entscheidung (das heißt β < 1 im Falle der Konvergenz bzw. α > 1 im Falle der Divergenz)
so liefert auch das Wurzelkriterium eine Entscheidung (das heißt β' < 1 im Falle der Konvergenz bzw. α' > 1 im Falle der Divergenz).
Dies wird induziert durch die Ungleichungskette
Ist ohne Einschränkung
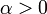 und
und 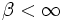 so gibt es zu jedem noch so kleinen (
so gibt es zu jedem noch so kleinen (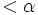 ) aber positivem
) aber positivem  eine Indexschranke
eine Indexschranke 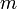 ab der gilt
ab der giltMultipliziert man die Ungleichung durch von
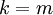 bis
bis 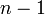 so erhält in der Mitte ein Teleskopprodukt.
so erhält in der Mitte ein Teleskopprodukt.Multipliziert man anschließend mit
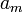 durch und zieht die
durch und zieht die 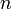 -te Wurzel so ist
-te Wurzel so istFür
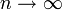 konvergiert die linke Seite gegen
konvergiert die linke Seite gegen 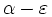 und die rechte Seite gegen
und die rechte Seite gegen 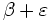 . Daher ist
. Daher ist![\alpha-\varepsilon\le \liminf \sqrt[n]{a_n}](/pictures/dewiki/53/56d67209f205e48d1c4c9858c460deb0.png) und
und ![\limsup \sqrt[n]{a_n}\le \beta+\varepsilon](/pictures/dewiki/57/9d1c88826f3affc96084f35590b54f54.png)
Das
 durfte anfangs beliebig gewählt klein gewählt werden daher
durfte anfangs beliebig gewählt klein gewählt werden daher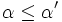 und
und 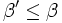
Sind beispielsweise die Reihenglieder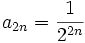 und
und 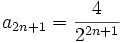 dann ist
dann ist 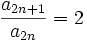 und
und 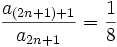 .
.Hier ist
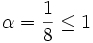 und
und 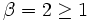 wonach das Quotientenkriterium keine Entscheidung liefert.
wonach das Quotientenkriterium keine Entscheidung liefert.Das Wurzelkriterium liefert hier aber eine Entscheidung weil
![\alpha'=\beta'=\lim \sqrt[n]{a_n}=\frac12](/pictures/dewiki/102/f99f4f0638da62ab637b6db01a23bdad.png) ist.
ist.Aus
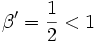 folgt die Konvergenz von
folgt die Konvergenz von 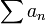 . Das Wurzelkriterium ist also echt schärfer als das Quotientenkriterium.[1]
. Das Wurzelkriterium ist also echt schärfer als das Quotientenkriterium.[1]Quellen
- ↑ Konrad Knopp. Theorie und Anwendung der unendlichen Reihen. 5. Auflage, Springer Verlag 1964, ISBN 3-540-03138-3. S 286, Satz 161
Wikimedia Foundation.

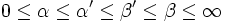
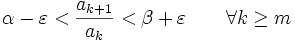
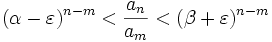
![\sqrt[n]{a_m}\,(\alpha-\varepsilon)^{1-\frac{m}{n}}&lt;\sqrt[n]{a_n}&lt;\sqrt[n]{a_m}\,(\beta+\varepsilon)^{1-\frac{m}{n}}](/pictures/dewiki/102/fede85b17fbfe9e907194b1a6e31a1d9.png)