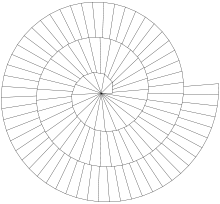
- Wurzelschnecke
-
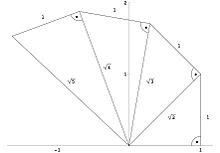
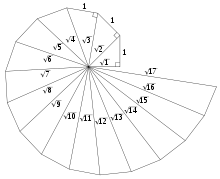
Die Wurzelschnecke oder Spirale des Theodorus ist eine Spirale, die von rechtwinkligen Dreiecken mit Seitenlängen 1,
 und
und  erzeugt wird.
erzeugt wird.Das erste Dreieck hat also die Seitenlängen 1,
 und
und  . Auf der Hypotenuse dieses Dreiecks wird das rechtwinklige Dreieck mit den Seitenlängen 1,
. Auf der Hypotenuse dieses Dreiecks wird das rechtwinklige Dreieck mit den Seitenlängen 1,  und
und  errichtet usw. Die aneinandergrenzenden Katheten bilden dann eine Spirale.
errichtet usw. Die aneinandergrenzenden Katheten bilden dann eine Spirale.Im Gegensatz zur Archimedischen oder Logarithmischen Spirale besteht die Wurzelschnecke aus Geradenstücken. Sie ist also nicht differenzierbar, lässt sich aber dafür exakt durch die abzählbar vielen Eckpunkte beschreiben.
1958 wurde von E. Teuffel bewiesen, dass sich niemals zwei der Hypotenusen decken werden, egal, wie weit man die Spirale zeichnet. Mit wachsender Windungszahl nähert sich die Wurzelschnecke asymptotisch einer Archimedischen Spirale an.
Weblink
Wikimedia Foundation.

 .
.