XTE

Querabweichung (engl. Cross Track Error, Abk.: XTE) beschreibt in der Navigation die Versetzung, gemessen senkrecht zur Verbindungsstrecke zwischen zwei Wegpunkten bzw. senkrecht zum Sollkurs. Eine weitere Bezeichnung ist auch Cross Track Distance (XTD).

Theorie

Eine Querabweichung entsteht, wenn die Strömungsrichtung des umgebenden Mediums (z.B. Luft oder Wasser) von der Wirkungsrichtung des Antriebes eines Fahr- oder Flugzeuges so abweicht, dass die Strömung nicht exakt von vorne oder von hinten wirkt.

Die mathematisch-physikalische Erklärung hierfür liegt in der Tatsache, dass die Wirkung zweier Kraftvektoren (hier: Antrieb und Strömung) auf das gleiche Objekt durch Vektoraddition einen neuen Gesamtkraftvektor bildet. Während die Gesamtbewegung des Objektes dem Gesamtkraftvektor folgt, resultiert die Querabweichung jedoch ausschließlich aus der Wirkung des Strömungsvektors. Wenn es sich beim Strömungsvektor um eine konstant wirkende Kraft handelt, steigt die Querabweichung mit der Zeit linear an. Es können erhebliche Abweichungen vom gewünschten Kurs entstehen.

Um einen Anstieg der Querabweichung zu vermeiden und diese möglichst bei Null zu halten, muss der Antriebsvektor so verändert werden, dass der aus der Addition von Antriebs- und Strömungsvektor resultierende Vektor dem gewünschten Steuerkurs entspricht. Dies wird erreicht, indem man den Strömungsvektor vom erwünschten Gesamtkraftvektor subtrahiert und als Ergebnis den benötigten Antriebsvektor erhält.

Beispiel: Ein Motor bewegt ein Boot mit 4 m/s nach Norden (0°). Die Strömung drückt mit 3 m/s von nach Osten (90°). Durch die Addition der Vektoren

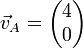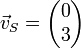$\vec v_A = \begin{pmatrix} 4 \\ 0 \end{pmatrix} \!\,$ und $\vec v_S = \begin{pmatrix} 0 \\ 3 \end{pmatrix} \!\,$ ergibt sich der Gesamtkraftvektor 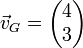$\vec v_G = \begin{pmatrix} 4 \\ 3 \end{pmatrix} \!\,$ für den tatsächlichen Kurs des Bootes, so dass das Boot nach dem Kosinussatz $\sqrt[2]{4^2 + 3^2}=\sqrt[2]{25}=5$ m/s Geschwindigkeit erreicht und dabei einen Kurs von 36,9°, also zwischen Nordost und Nordnordost beschreibt. Die Querabweichung hingegen beträgt nach einer Sekunde 3 Meter, nach 2 Sekunden 6 Meter usw. da für sie nur der Strömungsvektor relevant ist.

Da es nur in seltenen Fällen erwünscht ist, dass eine Strömung den Kurs bestimmt, muss der benötigte Antriebsvektor berechnet werden. Man subtrahiert wie folgt den Strömungsvektor vom gewünschten Gesamtkraftvektor:

$\vec v_G = \begin{pmatrix} 4 \\ 0 \end{pmatrix} \!\,-\vec v_S = \begin{pmatrix} 0 \\ 3 \end{pmatrix} \!\,=\vec v_A = \begin{pmatrix} 4 \\ -3 \end{pmatrix} \!\,$

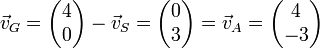
Nach dem Kosinussatz ergibt sich nun, dass der Motor mit 5 m/s in eine Richtung von 323,1° (360° - 36,9°) antreiben muss, um mit 4 m/s nach Norden zu fahren. Die so berechnete Richtung wird auch als Vorhaltewinkel bezeichnet.

Praktische Auswirkungen

Bei der Instrumentennavigation in der Luftfahrt, die mit Hilfe von Peilsendern durchgeführt wird, ist der Zielpunkt des Fluges bekannt, so dass man in einer Welt ohne Wind nur genau auf das Peilsignal zuhalten muss, um am gewünschten Ziel anzukommen. Durch die Auswirkungen eines Querwindes jedoch wird das Flugzeug von seinem gewünschten Kurs abgebracht, so dass der Pilot ständig die Richtung seines Flugzeuges ändern muss, um auf den Zielpunkt zuzufliegen. Die tatsächlich geflogene Strecke beschreibt hierdurch einen Bogen, der nicht nur den Treibstoffverbrauch erhöht, sondern auch eine mitunter gefährliche Abweichung vom geplanten Kurs sein kann.^[1] Es ist daher erstrebenswert, die Querabweichung jederzeit möglichst gering zu halten. Dies wird wie oben beschrieben erreicht, indem der vorherrschende Wind direkt in den Steuerkurs einbezogen wird. Ähnliches gilt auch in der Seefahrt.

Das Phänomen kann bei Fähren beobachtet werden, die einen Fluss überqueren. Die Fähre ist immer leicht schräg gegen die Strömung gestellt. Noch imposanter zeigt sich der Effekt bei Flugzeugen, die bei starkem Seitenwind landen. Vorhaltewinkel von 20° und mehr sind optisch gut als scheinbares "Schrägfliegen" zu beobachten.

Siehe auch

• Nautik
• Peilung
• Kurs (Navigation)

Quellen

1. ↑ Homing cross track error (eng.)