Relativistische Längenkontraktion

Die Lorentzkontraktion oder relativistische Längenkontraktion ist ein Phänomen der speziellen Relativitätstheorie. Für einen Beobachter sind Objekte umso kürzer, je schneller sie sich relativ zu ihm bewegen.

Ein solcher Effekt wurde ursprünglich als Ad-hoc-Hypothese in qualitativer Form von George Francis FitzGerald (1889) und in quantitativer Form von Hendrik Antoon Lorentz (1892) postuliert, um den negativen Ausgang des Michelson-Morley-Experiments zu erklären und dabei Idee eines ruhenden Äther zu retten (Fitzgerald-Lorentzsche Kontraktionshypothese). Albert Einstein hingegen gelang 1905 durch Reformulierung der Begriffe von Raum und Zeit und ohne einen Äther annehmen zu müssen, eine einfache Herleitung, welche dem Effekt den Ad-hoc-Charakter nahm und die Grundlage der modernen Erklärung bildet.

Erläuterung

Die Lorentzkontraktion besagt, dass eine Länge von verschiedenen Beobachtern unterschiedlich gemessen wird. Man betrachte zum Beispiel ein Raumschiff, das an der Erde mit einer konstanten Geschwindigkeit v vorbeifliegt. Der auf der Erde befindliche Beobachter wird im Folgenden als ruhender Beobachter bezeichnet, der Beobachter im Raumschiff als Reisender. Diese Begriffe sind allerdings nur als bequeme Bezeichnungen zu verstehen; aus Sicht des Reisenden ist der „ruhende“ Beobachter bewegt, während der Reisende selbst in seinem Raumschiff ruht. Der Reisende misst andere Entfernungen als der ruhende Beobachter:

$l=l_0 \cdot \sqrt{1-\frac{v^2}{c^2}}$.

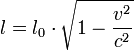Dabei bezeichnet l die Länge des Raumschiffs die der ruhende Beobachter misst, v ist die Geschwindigkeit des Raumschiffs, c ist die Lichtgeschwindigkeit, l₀ ist die Länge des Raumschiffes, die der mitreisende Beobachter misst. Dasselbe gilt auch umgekehrt: Fliegt der Reisende z.B. in Richtung Mond (der hier als unbewegt relativ zur Erde angenommen wird), dann gilt dieselbe Formel, wobei hier l₀ die Entfernung des Mondes zur Erde aus Sicht des auf der Erde ruhenden Beobachters, l hingegen die vom Reisenden bestimmte Entfernung.

Diese Kontraktion verkürzt also für den Reisenden Entfernungen, die er mit einem Raumschiff zurückzulegen hat. Für den ruhenden Beobachter bewegt sich das Raumschiff. Für ihn ändern sich die von dem Reisenden zurückzulegenden Entfernungen nicht, der Effekt der Längenkontraktion beschränkt sich für ihn auf das relativ zu ihm bewegte System, das Raumschiff. Das Raumschiff ist für den ruhenden Beobachter verkürzt.

Da für den Reisenden die zurückgelegte Strecke kürzer, der Betrag der Relativgeschwindigkeit v (Reisegeschwindigkeit) jedoch für beide Beobachter gleich ist, benötigt der Reisende aus seiner Sicht auch weniger Zeit, um diese Entfernung zurückzulegen, als aus Sicht des ruhenden Beobachters. Dies ist kein Widerspruch, da aufgrund der Zeitdilatation die Uhr des Reisenden aus Sicht des ruhenden Beobachters in der Tat langsamer läuft. Beide Beobachter stimmen also in ihrer Beobachtung überein, dass der Reisende weniger Zeit benötigt, als für die vom ruhenden Beobachter bestimmte Entfernung nötig wäre. Nur den Grund für diesen Unterschied geben sie unterschiedlich an: Der ruhende Beobachter schreibt den Effekt der durch die Zeitdilatation verlangsamten Eigenzeit des Reisenden zu, während der Reisende selbst die durch Lorentz-Kontraktion verkürzte Reisestrecke dafür verantwortlich macht.

Das „Garagen-Paradoxon“

Aus der Sicht der Garage

Aus der Sicht des Autos

Auf der Lorentz-Kontraktion beruht auch die Aussage, dass ein sehr schnell bewegtes Auto in eine viel zu kleine Garage passt. Andererseits hat sich für den Fahrer des Autos die Länge seines Autos nicht verändert, für ihn sind die Entfernungen verkürzt, die es zurückzulegen hat, insbesondere auch die Länge der Garage. Aus seiner Sicht passt das Auto also erst recht nicht in die Garage.

Die Auflösung des scheinbaren Paradoxons ergibt sich aus der Relativität der Gleichzeitigkeit. Um dies zu sehen, nehmen wir einmal an, die Garage habe auf beiden Seiten ein Tor, so dass das Auto bei geöffneten Toren hindurchfahren kann. Wenn nun das Auto kürzer ist als die Garage, können beide Tore gleichzeitig geschlossen werden, wenn das Auto sich darin befindet. Ist das Auto länger als die Garage, so ist dies natürlich nicht möglich, da das Auto auf mindestens einer Seite über die Garage hinausragt.

Um zu beweisen, dass das Auto in der Tat in die Garage passt, schließt der ruhende Beobachter beide Tore, sobald das Auto vollständig in der Garage ist, und öffnet die Tore gleich wieder, bevor das Auto das andere Garagentor erreicht hat (so dass das Auto nicht gegen das zweite Garagentor fährt). Aus seiner Sicht erfolgen also die wesentlichen Ereignisse in folgender Reihenfolge:

1. Das hintere Ende des Autos passiert das hintere Tor (das Auto befindet sich nun vollständig in der längeren Garage).
2. Beide Garagentore werden gleichzeitig geschlossen und sofort wieder geöffnet.
3. Das vordere Ende des Autos passiert das vordere Tor (das Auto beginnt also jetzt, die Garage wieder zu verlassen).

Da sich die Garagentore aber in Bewegungsrichtung des Autos an verschiedenen Orten befinden, ist aus Sicht des Autofahrers die Zeit des zuerst erreichten Garagentors gegenüber der des weiter vorne liegenden zweiten Garagentors verspätet. Aus seiner Sicht passiert also folgendes:

1. Das Tor an der Ausfahrt der Garage schließt sich und öffnet sich wieder, kurz bevor das Auto dieses Tor erreicht.
2. Anschließend passiert das vordere Ende des Autos das vordere Tor der (viel zu kurzen) Garage. Nun ragt das Auto auf beiden Seiten aus der Garage heraus.
3. Das hintere Ende des Autos passiert das hintere Tor.
4. Anschließend schließt sich das hintere Tor und öffnet sich sofort wieder.

Da aus Sicht des Autofahrers die beiden Tore niemals gleichzeitig geschlossen waren, konnte sein zu langes Auto die Garage passieren, ohne mit einem der Garagentore zusammenzustoßen.

Die optische Wahrnehmung der Lorentzkontraktion

Für den ruhenden Beobachter ist die Lorentzkontraktion als solche nicht erkennbar. Statt eines gestauchten Objektes sieht der Beobachter das ursprüngliche Objekt gedreht. Der scheinbare Drehwinkel ist von der Geschwindigkeit des Körpers abhängig.

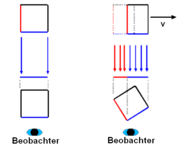
Der Grund für diesen Effekt lässt sich leicht an der nebenstehenden Grafik erläutern:

Lorentzkontraktion: optische Wahrnehmung als Drehung

Der betrachtete Körper ist hier vereinfacht als Würfel in der Draufsicht dargestellt, der ruhende Beobachter ist durch ein Auge symbolisiert. Die blaue Seite des Würfels befindet sich der Einfachheit wegen genau senkrecht zu Sichtlinie des Beobachters. Befindet sich nun der Körper in Ruhe, so sieht der Beobachter nur die Seite, die zu ihm zeigt (im Bild blau dargestellt)

Befindet sich der Körper allerdings in Bewegung (der Einfachheit wegen genau senkrecht zur Sichtlinie des Beobachters), so können auch die Lichtstrahlen, die von der roten Seite ausgehen, das Auge des Beobachters erreichen. Während die rote Seite bei einem ruhenden Körper unsichtbar ist, wird bei einem bewegten Körper mit zunehmender Geschwindigkeit immer mehr davon sichtbar.

Das sichtbare Bild eines Körpers wird durch die Lichtstrahlen bestimmt, die das Auge gleichzeitig erreichen. Während der Lichtstrahl vom hintersten Punkt der roten Seite auf dem Weg zum Beobachter an den weiter vorne liegenden Punkten vorbeikommt, hat sich der Körper schon ein Stück weiterbewegt. Somit kommen alle Lichtstrahlen von weiter vorne liegenden Punkten, die zur gleichen Zeit beim Auge eintreffen, in Bewegungsrichtung des Körpers versetzt beim Beobachter an – der Beobachter sieht also auch die rote Seite, allerdings gestaucht. Zugleich erscheint auch die blaue Seite gestaucht, da sie ja eine Lorentzkontraktion erfährt. Insgesamt ergibt sich für den Beobachter der gleiche optische Eindruck, den auch ein gedrehter Körper hervorruft. Der scheinbare Drehwinkel $\varphi$ ist hierbei nur von der relativen Geschwindigkeit v des Körpers senkrecht zur Sichtlinie des Beobachters abhängig: $\sin{\varphi} = \frac{v}{c}$

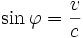
Einzelnachweise

• George Francis FitzGerald: The Ether and the Earth's Atmosphere. In: Science. 13, 1889, S. 390. doi:10.1126/science.ns-13.328.390

• Hendrik Antoon Lorentz: Die relative Bewegung der Erde und des Äthers. In: Abhandlungen über Theoretische Physik, S. 443-447, Leipzig: B.G. Teubner 1892/1907

• Albert Einstein: Zur Elektrodynamik bewegter Körper. In: Annalen der Physik. 322, Nr. 10, 1905, S. 891-921

Siehe auch

• Bellsches Raumschiffparadoxon
• Maßstabsparadoxon
• Geschichte der speziellen Relativitätstheorie

Weblinks

• http://itp.nat.uni-magdeburg.de/~kassner/srt/crashcourse/laengenkontraktion.html
• Beiträge zur Visualisierung der Längenkontraktion von der Universität Tübingen