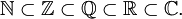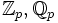- Zahlenraum
-
Eine Zahlenmenge ist eine genau definierte Menge von Zahlen. In der Regel werden unter diesem Begriff nicht nur die Elemente einer Menge verstanden, sondern auch die verschiedenen mathematischen Operationen, die man in diesen Mengen uneingeschränkt durchführen kann.
Dieser Artikel liefert einen Überblick über die gängigen Zahlenmengen, die in der Mathematik betrachtet werden.
Inhaltsverzeichnis
Übliche Zahlenmengen
Die Zahlenmengen wurden früher mit aufrecht stehenden fett gedruckten Großbuchstaben (also N, Z, Q, R, C, H usw.) bezeichnet. Um diese an der Tafel darzustellen, gingen Mathematiker dazu über, die Großbuchstaben mit doppelten Kreidestrichen darzustellen. Diese Darstellung wiederum fand dann Eingang in gedruckte Darstellungen. Heute ist in gedruckten mathematischen Lehrbüchern sowohl die Fettdruck- als auch die Doppelstrich-Variante verbreitet.
Natürliche Zahlen
Symbol:
 oder N
oder NNatürliche Zahlen werden sowohl verwendet, um die Anzahl von Dingen zu beschreiben, als auch, um Dinge zu ordnen. Die Menge umfasst die Zahlen 1, 2, 3, 4, 5, 6 usw. Zuweilen wird ihnen auch noch die neutrale Zahl 0 zugerechnet, manche Lehrbücher notieren diesen Zahlbereich dann als ℕ0. Addition und Multiplikation sind uneingeschränkt möglich.
In den natürlichen Zahlen 3 + 4 = 7, aber 3 - 4 ist in ℕ nicht wohldefiniert.
Eine wichtige Teilmenge der natürlichen Zahlen ist die Menge der Primzahlen, die manchmal mit
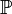 bezeichnet wird.
bezeichnet wird.Ganze Zahlen
Symbol:
 oder Z
oder ZDiese Zahlen erweitern die natürlichen Zahlen um negative ganze Zahlen. Mit ihnen ist es möglich, uneingeschränkt zu subtrahieren.
Beispiel: 3 - 4 = -1
Die Menge umfasst die Zahlen ... -3, -2, -1, 0, 1, 2, 3 ...
Rationale Zahlen
Symbol:
 oder Q
oder QDie rationalen Zahlen umfassen die Menge aller Bruchzahlen. Eine Bruchzahl ist der Quotient zweier ganzer Zahlen, wobei die Einschränkung gilt, dass der Divisor (=Nenner) nicht 0 sein darf. Mit der Erweiterung auf die rationalen Zahlen sind alle vier Grundrechenarten inklusive der Division ausführbar.
Beispiele:
 ,
, 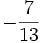 ,
, 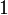 ,
, 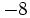
Reelle Zahlen
Symbol:
 oder R
oder RDie reellen Zahlen bilden eine Synthese aus den rationalen Zahlen und den so genannten irrationalen Zahlen - unendliche, nicht periodische und demzufolge nicht als Bruch darstellbare Zahlen. Das Ziehen der Wurzel bei positivem Radikand kann nun eindeutig durchgeführt werden.
Komplexe Zahlen
Symbol:
 oder C
oder CDie komplexen Zahlen sind der algebraische Abschluss der reellen Zahlen. Dies bedeutet, dass jedes Polynom eine Nullstelle hat. Es gibt folglich eine (nicht-reelle) Zahl
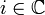 mit i2 + 1 = 0, die imaginäre Einheit. Komplexe Zahlen bestehen aus einem reellen und einem imaginären Teil. Um komplexe Zahlen zu multiplizieren benutzt man oft die Gaußsche Zahlenebene und die Polarform.
mit i2 + 1 = 0, die imaginäre Einheit. Komplexe Zahlen bestehen aus einem reellen und einem imaginären Teil. Um komplexe Zahlen zu multiplizieren benutzt man oft die Gaußsche Zahlenebene und die Polarform.Beispiele:
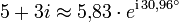
- 4 - 5i
Vergleich der Zahlenbereiche
Die genannten Zahlenbereiche sind Zahlbereichserweiterungen des jeweils vorhergehenden. Da jede Zahlenmenge eine echte Untermenge der erweiterten Zahlenmenge ist, spricht man hier von einer Inklusion.
Hyperkomplexe Zahlen
Das Konstruktionsverfahren zur Erzeugung der komplexen Zahlen kann verallgemeinert werden und liefert u.a. die folgenden Zahlbereiche.
Quaternionen oder Hamilton-Zahlen
Symbol:
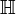 oder H
oder HDiese Zahlen, die durch die Elemente des Quaternionenrings dargestellt werden, sind die Erweiterung der komplexen Zahlen. Sie bilden in ihrer algebraischen Struktur nur einen Schiefkörper, da sie nicht kommutativ sind. Ihre Darstellung erfolgt in Form von drei Imaginärteilen.
Beispiele: 5 + 3i + 9j + 4k, -8 + 6i - 3j + 9k
Die komplexen Zahlen können auf viele verschiedene Arten als Teilmenge der Quaternionen aufgefasst werden: Ist I = xi + yj + zk mit x2 + y2 + z2 = 1, so ist
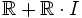 ein Körper, der isomorph zu den komplexen Zahlen ist. Alle diese so erhaltenen Teilkörper von
ein Körper, der isomorph zu den komplexen Zahlen ist. Alle diese so erhaltenen Teilkörper von  sind zueinander konjugiert.
sind zueinander konjugiert.Oktaven oder Oktonionen oder Cayley-Zahlen
Symbol:
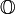 oder O
oder ODie Oktaven stellen eine achtdimensionale Erweiterung der reellen Zahlen (eine zweidimensionale Erweiterung des Quaternionenrings) dar. Ihre Multiplikation ist nicht mehr assoziativ, sondern nur noch alternativ. Sie sind der höchstdimensionale Zahlenbereich, in dem Division möglich ist, sie bilden eine Divisionsalgebra.
Beispiel: 7 + 8i + 3j - 12k + 4E - 8I - 9J + 12K
Da
 ,
,  ,
, 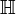 ,
, 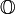 die einzigen normierten Divisionsalgebren sind, werden sie ebenfalls als Zahlen bezeichnet, obschon etwa bei
die einzigen normierten Divisionsalgebren sind, werden sie ebenfalls als Zahlen bezeichnet, obschon etwa bei 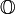 nicht einmal mehr die Assoziativität gilt.
nicht einmal mehr die Assoziativität gilt.Hyperrationale Zahlen
Die Konstruktionsverfahren zur Erzeugung der reellen Zahlen können verallgemeinert werden und liefern u.a.:
p-adische Zahlen Qp Hyperreelle Zahlen *R Surreale Zahlen Sω Weitere algebraische Strukturen, die manchmal Zahlen genannt werden
Sedenionen 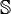
Restklassenkörper Z/pZ, p Primzahl Weblinks
- http://www.henked.de/begriffe/zahlenmengen.htm
- Skript zum Aufbau der Zahlbereiche (im PDF-Format, deutsch)
ZahlenbereicheNatürliche Zahlen
 | Ganze Zahlen
| Ganze Zahlen  | Rationale Zahlen
| Rationale Zahlen  | Reelle Zahlen
| Reelle Zahlen  | Komplexe Zahlen
| Komplexe Zahlen  | Quaternionen
| Quaternionen 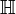 | Oktaven
| Oktaven 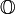
Wikimedia Foundation.

![\sqrt[]{2}, \sqrt[3]{17}](/pictures/dewiki/56/825986aba73430e824ac68167c15d153.png) ,
,