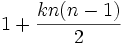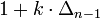Zentrierte Polygonale Zahl

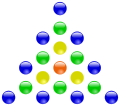
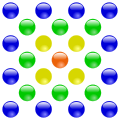
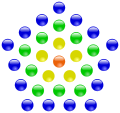
Eine zentrierte Polygonalzahl ist eine Zahl, zu der sich ein regelmäßiges Polygon (Vieleck) in einem bestimmten Muster und mit einer entsprechenden Zahl an Steinen legen lässt. Das Legemuster beginnt mit einem einzelnen Stein im Mittelpunkt des Polygons. Um diesen Zentrumsstein werden weitere Polygone gelegt, wobei sich deren Seitenlängen von innen nach außen jeweils um eins erhöhen. Abhängig von der Anzahl der Seiten spricht man beispielsweise von zentrierten Dreieckszahlen, zentrierten Quadratzahlen, zentrierten Fünfeckszahlen, zentrierten Sechseckszahlen, u.s.w. Die folgenden Bilder zeigen einige Beispiele.

Die 19 ist die vierte zentrierte Dreieckszahl.

Die 25 ist die vierte zentrierte Quadratzahl.

Die 31 ist die vierte zentrierte Fünfeckszahl.

Die 37 ist die vierte zentrierte Sechseckszahl.

Aufgrund ihrer Verwandtschaft mit einer geometrischen Figur zählen die zentrierten Polygonalzahlen zur Klasse der figurierten Zahlen. Eine andere Art, Zahlen auf Polygone zurückzuführen, stellen die (dezentralen) Polygonalzahlen dar.

Berechnung

Die n-te zentrierte k-Eckszahl berechnet sich nach der Formel

$1 + \frac{kn(n-1)}{2}$

Alternativ kann man die n-te zentrierte k-Eckszahl auch mit Hilfe der (n − 1)-ten Dreieckszahl Δ_{n − 1} nach der Formel

$1 + k \cdot \Delta_{n-1}$

berechnen.