Polygonalzahl

Eine Polygonalzahl ist ein Zahl, zu der es ein regelmäßiges Polygon (Vieleck) gibt, das sich mit einer entsprechenden Zahl an Steinen legen lässt. Beispielsweise ist die 16 eine Polygonalzahl, da sich ein Quadrat aus 16 Steinen legen lässt. Zu den Polygonalzahl zählen unter anderem die Dreiecks- und Quadratzahlen.

Die Polygonalzahl zählen zu den figurierten Zahlen. Eine andere Art, Zahlen auf Polygone zurückzuführen, stellen die zentrierten Polygonalzahlen dar.

Die Polygonalzahl lassen sich durch eine einfache Rechenvorschrift erzeugen. Man wählt dazu eine natürliche Zahl d als Differenz. Die erste Zahl ist jeweils die 1 und alle nachfolgenden Polygonalzahl entstehen, indem man jeweils die Differenz zur vorhergehenden hinzuaddiert. Die folgenden Beispiele zeigen dies.

Dreieckszahlen

Die Differenz 1 führt zu den Summen $1 + 2 + 3 + 4 + \ldots$, aus denen man die Dreieckszahlen $1, 3, 6, 10, \ldots$ erhält.

Quadratzahlen

Die Differenz 2 führt zu den Summen $1 + 3 + 5 + 7 + \ldots$, aus denen man die Quadratzahlen $1, 4, 9, 16, \ldots$ erhält.

Fünfeckszahlen

Die Differenz 3 führt zu den Summen $1 + 4 + 7 + 10 + \ldots$, aus denen man die Fünfeckszahlen $1, 5, 12, 22, \ldots$ erhält.

Sechseckszahlen

Die Differenz 4 führt zu den Summen $1 + 5 + 9 + 13 + \ldots$, aus denen man die Sechseckszahlen $1, 6, 15, 28, \ldots$ erhält.

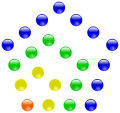
Die einzelnen Summanden sind jeweils die Folgenglieder einer arithmetischen Folge mit dem Anfangsglied 1 und der jeweiligen Differenz (vgl. Differenzenfolge). Dieser Aufbau der Polygonalzahl spiegelt sich auch in den entsprechenden Polygonen wider:

• 

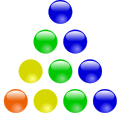
  Die 10 ist die vierte Dreieckszahl.

• 

  Die 16 ist die vierte Quadratzahl.

• 

  Die 22 ist die vierte Fünfeckszahl.

• 

  Die 28 ist die vierte Sechseckszahl.

Gelegentlich wird per Definition auch die 0 als 0-te Dreieckszahl, Quadratzahl, … eingeführt. Nach dieser Konvention lautet die Folge der Dreieckszahlen beispielsweise $0, 1, 3, 6, 10, \ldots$.

Berechnung

Die jeweils n-te k-Eckszahl lässt sich mit der Formel

${(k-2)n^2-(k-4)n}\over 2$

berechnen.

Liegt eine beliebige k-Eckszahl x vor, dann berechnet sich das zugehörige n nach der Formel

$n = \frac{\sqrt{8(k-2)x+(k-4)^2}+k-4}{2(k-2)}.$

Summe der Kehrwerte

Die Summe der Kehrwerte jeweils aller k-Eckszahlen ist konvergent.^[1] Es gilt:

$\sum_{n=1}^{\infty} \frac{2}{(k-2)n^2-(k-4)n} = \frac{2\ln{(2)} + \psi{(\frac{1}{k-2})} + \psi{(\frac{k}{2k-2})} + 2\gamma}{k-2}$

(vgl. ln , γ, ψ)

Anwendungen

Nach dem fermatschen Polygonalzahlensatz lässt sich jede Zahl als Summe von höchstens k k-Eckszahlen darstellen.

Literatur

• James Mitchell (Hrsg.): A Dictionary of the Mathematical and Physical Sciences, according to the latest Improvements and Discoveries. G. & W. S. Whittaker, London 1823, online.
• Constance Reid: From Zero to Infinity. What Makes Numbers Interesting. 4th edition. Mathematical Association of America, Washington DC 1992, ISBN 0-88385-505-4, Kapitel 5, online.
• Lawrence Downey, Boon W. Ong, James A. Sellers: Beyond the Basel Problem: Sums of Reciprocals of Figurate Numbers. online (PDF; 93 KB).

Weblinks

• Eric W. Weisstein: Polygonal Number. In: MathWorld. (englisch)
• Polygonalzahl bei PlanetMath (englisch)

Einzelnachweise

1. ↑ Siehe Artikel von Downey, Ong, Sellers.