Zentrierte Dreieckszahl

19 Kugeln in Form ineinandergeschachtelter Dreiecke

Eine zentrierte Dreieckszahl ist ein Zahl, die sich nach der Formel

$\frac{3n^2 + 3n + 2}{2}$

aus einer natürlichen Zahl n berechnen lässt. Die ersten zentrierten Dreieckszahlen sind

1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166, … (Folge A005448 in OEIS)

Die zentrierten Dreieckszahlen gehören wie die zentrierten Quadratzahlen sowie die zentrierten Fünf- und Sechseckszahlen zu den zentrierten Polygonalzahlen, also zu den ebenen figurierten Zahlen

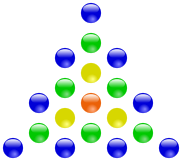
Die zentrierten Dreieckszahlen beziffern nämlich die Anzahl von Steinchen, um ein Dreieck nach folgender Vorschrift zu legen: Es befindet sich ein Steinchen im Zentrum und um dieses werden in dreiecksförmigen Schichten weitere Steinchen angeordnet. Die Anzahl der Steinchen in einer solchen Anordnung mit n Schichten wird als n-te zentrierte Dreieckszahl bezeichnet.

Für $n\geq 3$ lässt sich jede zentrierte Dreieckszahl als die Summe dreier aufeinander folgender normaler Dreieckszahlen darstellen. Des Weiteren gilt, dass eine Ganzzahldivision einer beliebigen Dreieckszahl ZD_n durch 3 immer den Rest 1 ergibt und als Quotient die vorhergehende Dreieckszahl ZD_{n − 1}.

Die Summe der ersten n Dreieckszahlen ($n\ge 2$) ergibt die magische Konstante (Zeilensumme) eines magischen Quadrates der Zahlen 1 bis n².

Zentrierte Dreiecksprimzahlen

Eine zentrierte Dreieckszahl, die eine Primzahl ist, wird als zentrierte Dreiecksprimzahl bezeichnet. Die ersten zentrierten Dreiecksprimzahlen lauten:

19, 31, 109, 199, 409, ... (Folge A125602 in OEIS)

Siehe auch

• Polygonalzahl

Quellen

• Lancelot Hogben: Mathematik für alle. Eine Einführung in die Wissenschaft der Zahlen und Figuren. Neu überarbeitete Ausgabe. Pawlak, Herrsching 1985, ISBN 3-88199-208-1, S. 151ff.
• Eric W. Weisstein: centered triangular number. In: MathWorld. (englisch)