Zentrierte Quadratzahl

25 Kugeln in Form ineinandergeschachtelter Quadrate

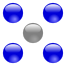
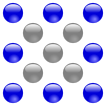
Eine zentrierte Quadratzahl ist ein Zahl, die die Summe zweier aufeinanderfolgender Quadratzahlen ist. Beispielsweise ist $13 = 4 + 9 = 2 2 + 3 2$ eine zentrierte Quadratzahl. Die ersten zentrierten Quadratzahlen sind

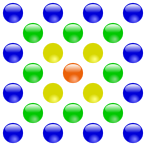
1, 5, 13, 25, 41, 61, 85, 113, 145, 181, 221, … (Folge A001844 in OEIS)

Eine zentrierte Quadratzahl beziffert eine Anzahl von Steinen, so dass ein Stein in der Mitte so von weiteren Steinen umgeben ist, dass diese ein Quadrat bilden.


1 Stein	5 Steine	13 Steine	25 Steine

Die $n$ -te zentrierte Quadratzahl $Z Q n$ berechnet sich nach der Formel

Z Q n = 2 n 2 + 2 n + 1

Inhaltsverzeichnis

1 Beziehungen zu anderen figurierten Zahlen
- 1.1 Dreieckszahlen
- 1.2 Quadratzahlen
2 Sonstiges
- 2.1 Abwandlungen und Verallgemeinungen
3 Siehe auch
4 Weblinks

Beziehungen zu anderen figurierten Zahlen

Dreieckszahlen

Die $n$ -te zentrierte Quadratzahl ist eine ungerade Zahl, die um eins größer ist als das Vierfache der $n$ -ten Dreieckszahl.

$ZQ_n = 1 + 4\Delta_n = 1 + 4\cdot \frac{n\cdot (n+1)}{2}$

Jede $n$ -te zentrierte Quadratzahl lässt sich als Summe von Dreieckszahlen erzeugen:

$ZQ_n = \Delta_{n-1} + 2\Delta_n + \Delta_{n+1}= \frac{(n-1)n}{2} + 2\cdot \frac{n(n+1)}{2} + \frac{(n+1)(n+2)}{2}$

Quadratzahlen

Jede zentrierte Quadratzahl ist die Summe zweier aufeinanderfolgender (dezentraler) Quadratzahlen. Dies wird offensichtlich, wenn man die Berechnungsformel für die zentrierten Quadratzahlen umstellt.

2 n 2 + 2 n + 1 = n 2 + (n + 1) 2

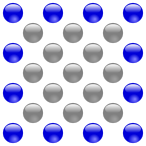
Auch an dem einer zentrierten Quadratzahl zugrundeliegenden Muster lässt sich dieser Sachverhalt erkennen:

Centered square number 13 as sum of two square numbers.svg

Sonstiges

Im Vergleich zu den Quadratzahlen, die stets zusammengesetzt sind, gibt es in der Folge der Zentrierten Quadratzahlen auch einige Primzahlen. Die ersten primen zentrierten Quadratzahlen sind

5, 13, 41, 61, 113, 181, 313, 421, 613, 761, 1013, … (Folge A027862 in OEIS).

Abwandlungen und Verallgemeinungen

Die dezentralen Quadrat- und Sechseckszahlen bzw. die Polygonalzahlen.
Oktaederzahlen sind die Summen der ersten zentrierten Quadratzahlen (sh. Figurierte Zahl).

Siehe auch

Weblinks

Eric W. Weisstein: Zentrierte Quadratzahl. In: MathWorld. (englisch)

Kategorie:

Figurierte Zahl

Wikimedia Foundation.

Игры ⚽ Нужна курсовая?

Schlagen Sie auch in anderen Wörterbüchern nach:

Quadratzahl — 16 Kugeln bilden ein Quadrat. Eine Quadratzahl ist eine Zahl, die durch die Multiplikation einer ganzen Zahl mit sich selbst entsteht. Beispielsweise ist eine Quadratzahl. Die ersten Quadratzahlen sind 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, …… … Deutsch Wikipedia
Zentrierte Polygonale Zahl — Eine zentrierte Polygonalzahl ist eine Zahl, zu der sich ein regelmäßiges Polygon (Vieleck) in einem bestimmten Muster und mit einer entsprechenden Zahl an Steinen legen lässt. Das Legemuster beginnt mit einem einzelnen Stein im Mittelpunkt des… … Deutsch Wikipedia
Zentrierte Polygonalzahl — Eine zentrierte Polygonalzahl ist eine Zahl, zu der sich ein regelmäßiges Polygon (Vieleck) in einem bestimmten Muster und mit einer entsprechenden Zahl an Steinen legen lässt. Das Legemuster beginnt mit einem einzelnen Stein im Mittelpunkt des… … Deutsch Wikipedia
Zentrierte Sechseckzahl — 37 Kugeln in Form ineinandergeschachtelter Sechsecke Eine zentrierte Sechseckszahl oder Hexzahl ist ein Zahl, die sich nach der Formel 3n2 + 3n + 1 aus einer natürlichen Zahl n berechnen lässt. Die ersten zentrierten Sechseckszahlen sind 1, 7, 19 … Deutsch Wikipedia
Dreieckszahl — Ein Dreieck aus zehn Steinen Eine Dreieckszahl ist eine Zahl, die der Summe aller Zahlen von 1 bis zu einer Obergrenze n entspricht. Beispielsweise ist die 10 eine Dreieckszahl, da 1 + 2 + 3 + 4 = 10 ist. Die ersten Dreieckszahlen sind 0, 1, 3, 6 … Deutsch Wikipedia
Figurat — Figurierte Zahlen sind Klassen von Zahlen, die sich auf geometrische Figuren beziehen. Legt man regelmäßige Figuren aus Spielsteinen und zählt die Steine, erhält man figurierte Zahlen. Beispiele für figurierte Zahlen sind die Quadratzahlen,… … Deutsch Wikipedia
Figurierte Zahl — Figurierte Zahlen sind Klassen von Zahlen, die sich auf geometrische Figuren beziehen. Legt man regelmäßige Figuren aus Spielsteinen und zählt die Steine, erhält man figurierte Zahlen. Beispiele für figurierte Zahlen sind die Quadratzahlen,… … Deutsch Wikipedia
Bäckerdutzend — beim Pferderennen im Santa Anita Park fehlt eine Startbox mit der Zahl 13 Ein Fahrstuhl in Buenos Aires ohne 13. Stock. Dreizehn i … Deutsch Wikipedia
Nombre Carré Centré — Un nombre carré centré est un nombre figuré centré qui peut être représenté par un carré ayant un point en son centre et d autres points placés autour du centre à une certaine distance (associée à la norme 1.) comme dans l exemple suivant :… … Wikipédia en Français
Nombre carre centre — Nombre carré centré Un nombre carré centré est un nombre figuré centré qui peut être représenté par un carré ayant un point en son centre et d autres points placés autour du centre à une certaine distance (associée à la norme 1.) comme dans l… … Wikipédia en Français

Academic dictionaries and encyclopedias

Zentrierte Quadratzahl

Inhaltsverzeichnis