Quadratzahl

16 Kugeln bilden ein Quadrat.

Eine Quadratzahl ist eine Zahl, die durch die Multiplikation einer ganzen Zahl mit sich selbst entsteht. Beispielsweise ist $144 = 12 \cdot 12$ eine Quadratzahl. Die ersten Quadratzahlen sind

0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, … (Folge A000290 in OEIS)

Bei einigen Autoren ist die Null keine Quadratzahl, sodass die Zahlenfolge erst mit der Eins beginnt.

Die Bezeichnung Quadratzahl leitet sich von der geometrischen Figur des Quadrats her. Die Anzahl der Steine, die man zum Legen eines Quadrats benötigt, ist immer eine Quadratzahl. So lässt sich beispielsweise ein Quadrat mit der Seitenlänge 4 mit Hilfe von 16 Steinen legen.

Aufgrund dieser Verwandtschaft mit einer geometrischen Figur zählen die Quadratzahlen zu den figurierten Zahlen, zu denen auch die Dreieckszahlen und Kubikzahlen gehören. Diese Begriffe waren schon den griechischen Mathematikern der Antike bekannt.^[1]

Eigenschaften

Gerade Quadratzahlen sind das Quadrat gerader Zahlen, während ungerade Quadratzahlen das Quadrat ungerader Zahlen sind.

Formeln zum Generieren von Quadratzahlen

Jede Quadratzahl n² ist die Summe der ersten n ungeraden natürlichen Zahlen.

$\begin{align} &1 &= 1 &=1^2\\ &1 + 3 &= 4 &= 2^2\\ &1 + 3 + 5 &= 9 &= 3^2\\ &1 + 3 + 5 + 7 &= 16 &= 4^2\\ & & \vdots & \end{align}$

Diese Gesetzmäßigkeit wird durch die folgenden Bilder veranschaulicht.

$0 + \color{blue}1 \color{black}= 1$	$1 + \color{blue}3 \color{black}= 4$	$4 + \color{blue}5 \color{black}= 9$	$9 + \color{blue}7 \color{black}= 16$

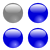
Von links nach rechts sind hier die ersten vier Quadratzahlen durch die entsprechende Anzahl an Kugeln dargestellt. Die blauen Kugeln zeigen jeweils den Unterschied zur vorhergehenden Quadratzahl an. Da von links nach rechts immer eine Reihe und eine Zeile hinzukommt, erhöht sich die Anzahl der blauen Kugeln jeweils um 2. Beginnend mit der 1 ganz links durchlaufen die blauen Kugeln so alle ungeraden Zahlen.

Das Bildungsgesetz lässt sich auch direkt mit Hilfe der ersten binomischen Formel beweisen. Dazu werden die entsprechenden Summen durch die Formel

$n^2 = \sum^n_{i=1} (2i-1) = 1 + 3 + 5 + \dots + (2n-1)$

dargestellt. Durch vollständige Induktion lässt sich deren Gültigkeit zeigen. Der Induktionsanfang

$1^2 = \sum^1_{i=1} 2i -1 = 2 \cdot 1 - 1 = 1$

für n = 1 ist offensichtlich richtig. Unter der Annahme, dass

$n^2 = \sum^n_{i=1} (2i-1)$

gilt, ist dann auch der Induktionsschluss

$\begin{align} (n+1)^2 &= n^2 + 2n + 1\\ &= \bigl( \sum^n_{i=1} (2i-1) \bigr) + 2n + 1\\ &= \bigl( \sum^n_{i=1} (2i-1) \bigr) + 2(n + 1) - 1\\ &= \sum^{n+1}_{i=1} (2i-1) \end{align}$

gültig.

Trick zum Berechnen von Fünfer-Quadratzahlen im Kopf

Das Quadrat von Zahlen, die auf 5 enden, lässt sich leicht im Kopf berechnen. Man multipliziert die Zahl ohne die Einerziffer 5 (z. B. bei 45 die 4) mit ihrem Nachfolger (hier 4+1 = 5) und hängt an das Produkt (hier 4·5 = 20) die Ziffern 2 und 5 an (Endergebnis 2025).

$\underline{1}5^2 = \underline{2}25$

$\underline{2}5^2 = \underline{6}25$

$\underline{3}5^2 = \underline{12}25$

$\underline{4}5^2 = [4 \cdot (4+1)]25 = \underline{20}25$

$[a]5^2 = [a \cdot (a+1)]25$

Beweis: Eine Fünferzahl lässt sich darstellen als $10 \cdot k+5, k \in \mathbb{N}$. Ihr Quadrat ist somit $(10 \cdot k+5)^2 = 100k^2+100k+25 = 100 \cdot k(k+1)+25$.

Beziehungen zu anderen figurierten Zahlen

Dreieckszahlen

10 + 15 = 25

Jede Quadratzahl lässt sich als Summe zweier aufeinanderfolgender Dreieckszahlen darstellen. Das nebenstehende Bild zeigt beispielhaft, wie sich die Quadratzahl 25 als Summe der Dreieckszahlen Δ₄ = 10 und Δ₅ = 15 ergibt.

Dieses Phänomen lässt sich auch durch eine Formel beschreiben.

$\begin{align} n^2 &= \frac{n(n-1)}{2} + \frac{(n+1)n}{2}\\ &= \Delta_{n-1} + \Delta_n\\ \end{align}$

Zentrierte Quadratzahlen

Neben dem den Quadratzahlen zugrundeliegenden Muster gibt es noch ein zweites Muster, um ein Quadrat zu legen. Dabei werden um einen Stein in der Mitte des Quadrats weitere Quadrate gelegt. Die für diese Muster notwendige Anzahl an Steinen entspricht jeweils einer zentrierten Quadratzahl. Jede zentrierte Quadratzahl ist die Summe zweier aufeinanderfolgender Quadratzahlen, wie sich an deren geometrischen Muster erkennen lässt.

Auch die Formel für zentrierte Quadratzahlen lässt sich mit Hilfe der ersten binomischen Formel so umstellen, dass die beiden Quadratzahlen sichtbar werden.

$\begin{align} 2n^2 + 2n + 1 &= n^2 + (n^2 + 2n + 1) \\ &=n^2 + (n+1)^2 \end{align}$

Pyramidenzahlen

Die Summe der ersten n Quadratzahlen ergibt die n-te Pyramidenzahl.

$\sum^n_{i=1} (i^2) = 1^2 + 2^2 + 3^2 + \dots + n^2 = \frac{n(n+1)(2n+1)}{6}$

Das folgende Bild veranschaulicht diese Beziehung am Beispiel der vierten Pyramidenzahl.

Endziffern von Quadratzahlen

Quadratzahlen enden nie mit einer der Ziffern 2, 3, 7 oder 8, da kein Quadrat einer einstelligen Zahl mit einer dieser Ziffern endet.

Ist y die letzte Ziffer einer beliebigen Zahl $a = 10 \cdot x + y$, dann gilt für deren Quadrat

$a^2 = 100 \cdot x^2 + 20 \cdot xy + y^2$

Die letzte Ziffer von a² ist somit identisch mit der letzten Ziffer von y². Unter den ersten Quadratzahlen 0, 1, 4, 9, 16, 25, 36, 49, 64 und 81 findet sich jedoch keine Zahl, die auf 2, 3, 7 oder 8 endet.

Teileranzahl

Nur Quadratzahlen haben eine ungerade Anzahl von Teilern. Beweis: Ist a < n ein Teiler der Quadratzahl n², dann gibt es einen zweiten Teiler b > n mit $a \cdot b = n^2$. Die Menge aller a und b enthält eine geradzahlige Anzahl von Elementen. Neben den Elementen dieser Menge ist nur noch n ein Teiler von n². Die Teilermenge hat deshalb eine ungerade Anzahl von Elementen.

Reihe der Kehrwerte

→ Hauptartikel: Basler Problem

Die Summe der Kehrwerte aller Quadratzahlen ist

$\sum_{n=1}^{\infty} \frac{1}{n^2} = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \dots = \frac{\pi^2}{6}$ .

Es war lange Zeit nicht bekannt, ob diese Reihe konvergiert. Erst Leonhard Euler fand im Jahr 1735 den Wert der Reihe.

Siehe auch

• Vier-Quadrate-Satz

Weblinks

 Commons: Square numbers – Sammlung von Bildern, Videos und Audiodateien

Einzelnachweise

1. ↑ Helmuth Gericke: Mathematik in Antike, Orient und Abendland. Marix Verlag, Wiesbaden 2005, ISBN 3-937715-71-1, S. 142–143