- Disjunkte Wege
-
Wege, Pfade, Zyklen und Kreise sind Begriffe der Graphentheorie und beschreiben im Allgemeinen eine spezielle, zusammenhängende Folge von Knoten in einem Graphen. Da die Begriffe eng miteinander verwandt sind, werden sie in diesem Übersichtsartikel zusammen dargestellt.
Inhaltsverzeichnis
Definitionen
Gerichtete und ungerichtete Wege
Sei G = (V,E) ein (gerichteter) (Multi-)Graph und
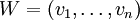 eine Folge von Knoten aus V mit der Eigenschaft, dass für alle i aus
eine Folge von Knoten aus V mit der Eigenschaft, dass für alle i aus 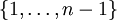 gilt:
gilt:- Die Menge {vi,vi + 1} ist Element von E, falls G ein ungerichteter Graph ohne Mehrfachkanten ist.
- Das Paar (vi,vi + 1) ist Element von E, falls G ein gerichteter Graph ohne Mehrfachkanten ist.
- E({vi,vi + 1}) > 0, falls G ein ungerichteter Graph mit Mehrfachkanten ist.
- E({vi,vi + 1}) > 0, falls G ein gerichteter Graph mit Mehrfachkanten ist.
Das heißt vi und vi + 1 sind durch eine Kante verbunden. Dann bezeichnet man W als ungerichteten Weg in G, falls G ungerichtet ist, und als gerichteten Weg in G, falls G gerichtet ist. Eine andere Bezeichnung für Weg ist Kantenfolge. Den Knoten v1 nennt man Startknoten von W und den Knoten vn Endknoten von W. Einen besonderen Weg stellt der Eulersche Weg dar.
Pfade, Zyklen und Kreise
Einen Weg W bezeichnet man als
- Pfad, falls alle Knoten in der Folge W voneinander verschieden sind, das heißt falls für alle i und j aus
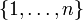 gilt, dass
gilt, dass 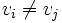 , falls
, falls 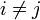 .
. - Zyklus, falls Start- und Endknoten von W identisch sind, das heißt falls v1 = vn.
- Kreis, falls nur Start- und Endknoten von W identisch sind, das heißt falls v1 = vn und
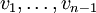 einen Pfad bilden, also für alle i und j aus
einen Pfad bilden, also für alle i und j aus 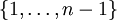 gilt, dass
gilt, dass 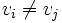 , falls
, falls 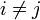 .
.
Bemerkung: Jeder Kreis, Zyklus oder Pfad in einem Graphen G ist also auch ein Weg und jeder Kreis ist auch ein Zyklus in G. Wege, Pfade, Zyklen und Kreise definiert man alternativ auch über Kantenzüge oder Teilgraphen. Gibt es einen Weg von Knoten u zu Knoten v in G, so heißt v von u aus erreichbar (Erreichbarkeitsproblem in Graphen).
In ungerichteten Wegen und Pfaden bezeichnet man den Startknoten meist ebenfalls als Endknoten. In Zyklen und Kreisen verwendet man die Bezeichnungen Startknoten und Endknoten meist nicht.
Graphen mit Zyklen heißen zyklisch. Graphen ohne Zyklen heißen azyklisch. Ein Zyklus oder Kreis heißt trivial, wenn er weniger als drei Knoten enthält. Triviale Kreise oder Zyklen werden meist nicht betrachtet. Ein Kreis, der genau drei Knoten enthält nennt man oft Dreieck. Einen Graphen ohne Dreieck nennt man dann dreiecksfrei.
A-B-Weg, v-w-Weg, a-B-Fächer
Sind A und B Teilmengen von V, so bezeichnet man einen Weg als A-B-Weg, falls der Startknoten in A und der Endknoten in B liegt. Statt von einem {v}-{w}-Weg spricht man auch von einem v-w-Weg. Eine Menge von a-B-Wegen nennt man einen a-B-Fächer, wenn die Wege paarweise nur den Knoten a gemeinsam haben.
Kreuzungsfrei, knotendisjunkt, kantendisjunkt
Zwei Wege
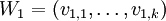 und
und 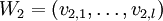 heißen kreuzungsfrei, knotendisjunkt oder einfach nur disjunkt, falls es kein Paar (i,j) mit i aus
heißen kreuzungsfrei, knotendisjunkt oder einfach nur disjunkt, falls es kein Paar (i,j) mit i aus 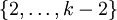 und j aus
und j aus 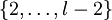 gibt, so dass v1,i = v2,j, das heißt, wenn sie keine inneren Knoten gemeinsam haben. Eine Menge von Wegen nennt man kreuzungsfrei, knotendisjunkt oder disjunkt, wenn die Wege paarweise disjunkt sind. Zwei Wege
gibt, so dass v1,i = v2,j, das heißt, wenn sie keine inneren Knoten gemeinsam haben. Eine Menge von Wegen nennt man kreuzungsfrei, knotendisjunkt oder disjunkt, wenn die Wege paarweise disjunkt sind. Zwei Wege 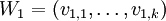 und
und 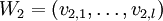 heißen kantendisjunkt, falls es kein Paar (i,j) mit i aus
heißen kantendisjunkt, falls es kein Paar (i,j) mit i aus 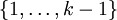 und j aus
und j aus 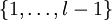 gibt, so dass v1,i = v2,j und v1,i + 1 = v2,j + 1. Eine Menge von Wegen nennt man kantendisjunkt, wenn die Wege paarweise kantendisjunkt sind.
gibt, so dass v1,i = v2,j und v1,i + 1 = v2,j + 1. Eine Menge von Wegen nennt man kantendisjunkt, wenn die Wege paarweise kantendisjunkt sind.Länge eines Weges (Zyklus, Kreises), Abstand
In Graphen ohne Gewichte auf den Kanten bezeichnet man mit n − 1 die Länge eines Weges (oder Pfades) und mit n die Länge eines Zyklus (oder Kreises)
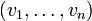 . Anschaulich zählt man also die Anzahl zugehöriger Kanten.
. Anschaulich zählt man also die Anzahl zugehöriger Kanten.In kantengewichteten Graphen bezeichnet man als Länge eines Weges die Summe der Kantengewichte aller zugehörigen Kanten.
Als einen kürzesten Weg von einem Knoten s zu einem Knoten t in einem Graphen bezeichnet man einen Weg von s nach t, dessen Länge minimal ist. Die Länge eines kürzesten Weges nennt man dann Abstand oder Distanz von s nach t. Falls kein Weg zwischen zwei Knoten existiert, so setzt man den Abstand auf unendlich.
Man beachte, dass in gerichteten Graphen der Abstand von der Richtung des Weges abhängt. Insbesondere kann es sein, dass nur in eine Richtung ein gerichteter Weg existiert.
Durchmesser und Taillenweite
Den größten Abstand zwischen zwei Knoten in einem Graphen G nennt man Durchmesser von G. Als Taillenweite eines Graphen bezeichnet man die Länge eines kürzesten nicht trivialen Kreises. Falls der Graph keinen Kreis besitzt, so setzt man die Taillenweite auf unendlich.
Distanzgraph
Der Distanzgraph zu einem Graphen G = (V,E) bezeichnet den vollständigen (das heißt je zwei Knoten sind durch eine Kante verbunden, ggf. in gerichteten Graphen in beide Richtungen, wobei es aber keine Schleifen gibt) kantengewichteten Graphen auf der Knotenmenge V, der jeder Kante als Kantengewicht den Abstand zwischen den beiden Knoten in G zuordnet.
Wichtige Algorithmen
Der Algorithmus von Dijkstra findet einen kürzesten Pfad zwischen zwei beliebigen Knoten in einem (kantengewichteten) Graphen. Mit seiner Hilfe lässt sich auch der Distanzgraph bestimmen, indem man ihm ausgehend von jedem Knoten den Abstand zu jedem anderen bestimmt. Für jeden Knoten ist dabei nur ein Aufruf des Algorithmus von Dijkstra nötig, da dieser auch den Abstand von einem Knoten zu allen anderen Knoten bestimmen kann.
Weitere Algorithmen zum Finden von kürzesten Pfaden sind der Algorithmus von Floyd und Warshall, der Algorithmus von Bellman und Ford und der Algorithmus von Johnsons, welcher Bellman-Ford mit Dijkstras Algorithmus kombiniert.
Der Distanzgraph ist für das Problem des Handlungsreisenden interessant, da dieser metrisch ist, weshalb verschiedene Approximationsalgorithmen die optimale Lösung dieses Problems approximieren können.
Siehe auch
Wikimedia Foundation.
