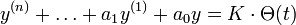Übergangsfunktion

Die Sprungantwort oder Übergangsfunktion ist das Ausgangssignal eines eindimensionalen, linearen, zeitinvarianten Systems, dem am Eingang die Heaviside-Funktion (auch Sprungfunktion genannt) zugeführt wird. Da die Sprungantwort über die Laplacetransformation mit der Übertragungsfunktion verbunden ist, kann die Übertragungsfunktion (näherungsweise) aus der Sprungantwort ermittelt werden. Im Vergleich zur Impulsantwort ist dabei vorteilhaft, dass ein Sprung als Eingangsgröße bei einem realen Aufbau in der Regel einfacher als ein Impuls zu verwirklichen ist. Damit ist die Sprungantwort eine wichtige Kenngröße des Systemverhaltens.

Mathematische Beschreibung

Ein System sei durch die Differentialgleichung

$y^{(n)} + \ldots + a_{1}y^{(1)} + a_{0}y = K\cdot \Theta(t)$

mit Θ(t) = 1 für 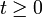$t \ge 0$ und Θ(t) = 0 für t < 0 beschrieben.

Die Sprungantwort a(t) lässt sich auch als Faltung der Sprungfunktion σ mit der Impulsantwort h berechnen: $a(t) = (h*\sigma)(t) = \int\limits_{ - \infty }^\infty {h(\tau )\sigma (t - \tau )} d\tau = \int\limits_{ - \infty }^t {h(\tau )} d\tau$

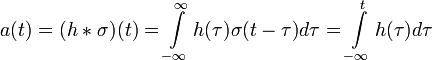
Die Sprungantwort ist somit das zeitliche Integral der Impulsantwort.

Im diskreten: $a[t] = (h*\sigma)[t] = \sum^\infty_{k=-\infty } h[n-k]\sigma[k] = \sigma[n] \sum^\infty_{k=0} h[n-k]$

Beispiel

Sprungantwort eines RC-Systems (Tiefpass)

Die Sprungfunktion eignet sich für ein System als Testsignal. Wenn am Eingang einer elektronischen Schaltung eine Sprungfunktion mit der Höhe 2V anlegt wird, dann kann man am Ausgang des Übertragungsgliedes ebenfalls eine Veränderung der Spannung feststellen. Den zeitlichen Verlauf dieser Spannung nennt man Sprungantwort, es ist also die Antwort des Systems auf die angelegte Sprungfunktion. Auf dem Bild sieht man, wie das Ausgangssignal sich langsam dem Wert am Eingang annähert. Wenn die Sprungantwort so aussieht wie auf dem Bild, lässt sich auf ein System mit einem Speicher schließen. Der Speicher ist in diesem Fall ein Kondensator. Dieser wird durch die 2V am Eingang über den Widerstand geladen, bis die Eingangsspannung erreicht ist. Das System verhält sich wie ein PT1-Glied.

Siehe auch

• Überschwingen

Literatur

• R. Parthier: Messtechnik – Grundlagen und Anwendungen der elektrischen Messtechnik für alle technischen Fachrichtungen und Wirtschaftsingenieure (4. Auflage – vieweg Verlag), ISBN 978-3-8348-0336-8