Regelungstechnik

Regelungstechnik ist eine Ingenieurwissenschaft, die alle in der Technik vorkommenden Regelungs-Vorgänge behandelt. Sie tangiert oder ist Bestandteil zahlreicher anderer Wissenschaften wie Kybernetik, Robotik, Automatisierungstechnik, Prozessinformatik, Verfahrenstechnik, Kontrolltheorie, Medizintechnik, Messtechnik, Fertigungstechnik aber auch Wasserwirtschaft, Biologie und Soziologie und andere.

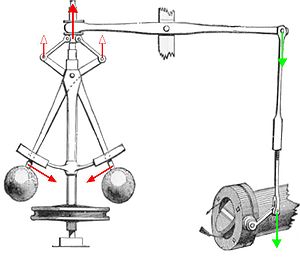Regelung der Drehzahl einer Dampfmaschine (nicht gezeichnet) mit einem Fliehkraftregler
rechts: Stellglied (Drosselklappe in der Dampfzuleitung)
links: Messglied und Regler als Einheit (Fliehkraftpendel auf einer Drehzahl-Messwelle)
Mitte: Rückkopplung (Hebel und Stange) = Gegenkopplung (kleinere Drehzahl vergrößert die Drosselöffnung), Sollwert-Veränderung durch Längenänderung der Stange

Fachlich anspruchsvolle Anwendungen sind beispielsweise Autopiloten in der Luftfahrt, Schifffahrt und Raumfahrt oder Antiblockiersystem und Tempomat in der Kraftfahrzeugtechnik. Bekannte Anwendungen im Haushalt findet man von der Heizungsregelung bis zum einfachen Zweipunktregler im Kühlschrank, Bügeleisen und Wasserkocher.

Die Regelungstechnik befasst sich mit der gezielten Beeinflussung von physikalischen, chemischen, biologischen oder anderen Größen in Geräten, Anlagen, Fahrzeugen mittels des Prinzips der Rückkopplung, so dass das Verhalten dieser Größen einem gewünschten Verhalten möglichst nahe kommt. Die Regelungstechnik stützt sich stark auf die Denkweisen und Methoden der Systemtheorie mit mathematischen Übertragungsmodellen.

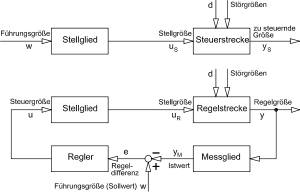
Mit Hilfe des Blockschaltbildes wird eine von allen physikalischen Details abstrahierte einheitliche Form der mathematischen Modelle der Regelkreiskomponenten dargestellt. Dazu gehören die Modell-Beschreibungen als Differenzialgleichung, der Übertragungsfunktion, der Zustandsraumdarstellung und der zeitdiskreten Numerischen Mathematik.

Im Gegensatz zur Steuerungstechnik, bei der der Datenfluss stets vorwärts gerichtet ist, besteht eine Regelung aus einem vorwärts gerichteten Zweig (Führungsgröße + Regler + Regelstrecke + Regelgröße) und einem rückwärts gerichteten Zweig (Rückführung der Regelgröße mit Messglied), die einen Kreis des Signalflusses bilden. Die zurückgeführte Regelgröße bildet mit der Führungsgröße eine Regeldifferenz, die auf den Regler wirkt.

Weil die Anwendung der Regelungstechnik ohne Kenntnisse der Steuerungstechnik und der Messtechnik nicht möglich ist, hat sich aus den Anfangsbuchstaben dieser Techniken dafür ein neuer Fachbegriff etabliert - MSR-Technik als Fachbereich.

Tabellarischer Zusammenhang der regelungstechnischen Artikel

Der Artikel Regelungstechnik steht als Überbegriff für alle regelungstechnischen Verfahren, Beschreibungen und Anwendungen.

Der elementare Systembegriff ist das dynamische System mit verteilten und / oder konzentrierten Energiespeichern (Feder-Masse-System, elektrisches RCL-System). Ein solches System hat für ein gegebenes Eingangssignal je nach Art der Anzahl der Systemspeicher, je nach deren Zustand (Anfangswerte) und Koeffizienten ein bestimmtes Zeitverhalten der Systemausgangsgröße.

Ist das dynamische System eine Regelstrecke, dann bestimmt der gewählte Regler mit Hilfe des zurückgeführten System-Ausgangssignals auf den Regelstrecken-Eingang und des Soll-Ist-Vergleiches das Systemverhalten des Regelkreises.

Die mathematische Beschreibung der Regelkreiskomponenten ist meist Bestandteil des Fachgebietes der Systemtheorie (Ingenieurwissenschaften). In diesem Fachgebiet wird die Systembeschreibung, die Systemanalyse, die Systemsynthese, die Erstellung des mathematischen Modells und die Berechnung in verschiedensten mathematischen Darstellungsformen behandelt.

Einzelne System-Beschreibungsformen wie die Differenzialgleichung, die Zustandsraumdarstellung, die Übertragungsfunktion und die zeitdiskrete numerische Darstellung stellen sich je nach gewünschter Ausführlichkeit als umfangreiche mathematische Teilgebiete dar.

Die nachfolgende Tabelle zeigt die wichtigsten Fachkapitel der Hauptartikel der Regelungstechnik und die im engen Zusammenhang stehenden Hauptartikel der Systembeschreibungen:

Artikel der $\underline {Regelungstechnik} \,$			Artikel der $\Longleftrightarrow \quad \underline {Systembeschreibungen} \,$
$\downarrow$ Artikel Regelstrecke	$\downarrow$ Artikel Regler	$\downarrow$ Artikel Regelkreis	$\downarrow$ Artikel Zustandsraum- darstellung	$\downarrow$ Artikel Systemtheorie (Ingenieurwissensch.)	$\downarrow$ Artikel Übertragungsfunktion (Laplacetransformation)
$\downarrow$ Kapitel Charakterisierung Regelstrecke	$\downarrow$ Kapitel Stetige Regler	$\downarrow$ Kapilel Einschleifiger Regelkreis	$\downarrow$ Kapitel Grundlagen Zustandsraum	$\downarrow$ Kapitel Dynamische Systeme	$\downarrow$ Kapitel Darstellungsformen Übertragungsfunktion
$\downarrow$ Kapitel Lineare Regelstrecken	$\downarrow$ Kapitel Zustandsregler	$\downarrow$ Kapilel Stabilität Regelkreis	$\downarrow$ Kapitel Zustandsraum- modell	$\downarrow$ Kapitel Lineare Prozesse im Zeitbereich	$\downarrow$ Kapitel Polynom- Darstellung
$\downarrow$ Kapitel Nichtlineare Übertragungssysteme	$\downarrow$ Kapitel Regler für Mehr- größensysteme	$\downarrow$ Kapilel Bewertung Stabilitätsverfahren	$\downarrow$ Kapitel Normalformen Zustandsraum	$\downarrow$ Kapitel Zeitverhalten element. Übertragungsglieder	$\downarrow$ Kapitel Pol-Nullstellen- Darstellung
$\downarrow$ Kapitel Testsignale	$\downarrow$ Kapitel Nichtlineare Regler	$\downarrow$ Kapilel Reglerentwurf LZI-Systeme	$\downarrow$ Kapitel Steuerbarkeit und Beobachtbarkeit	$\downarrow$ Kapitel Mathemaische Modelle	$\downarrow$ Kapitel Zeitkonstanten- Darstellung
$\downarrow$ Kapitel Experimentelle Systemidentifikation	$\downarrow$ Kapitel Unstetige Regler	$\downarrow$ Kapilel Reglerentwurf Totzeitregelstrecken	$\downarrow$ Kapitel Regelung Zustandsraum	$\downarrow$ Kapitel Gewöhnliche Differenzialgleichungen	$\downarrow$ Kapitel Partialbruch- Darstellung
$\downarrow$ Kapitel Stabilität Streckenglieder	$\downarrow$ Kapitel Realisierung von Reglern	$\downarrow$ Kapilel Regelung Zustandsraum	$\downarrow$ Kapitel Mathematisches Konzentrat	$\downarrow$ Kapitel Übertragungsfunktion	$\downarrow$ Kapitel Pole- Nullstellen- Zeitverhalten
$\downarrow$ Kapitel Regelstrecke Zustandsraum	$\downarrow$ Kapitel	$\downarrow$ Kapilel Regelkreis unstetige Regler	$\downarrow$ Kapitel	$\downarrow$ Kapitel Numerische Berechnung	$\downarrow$ Kapitel
$\downarrow$ Kapitel Mehrgrößensysteme	$\downarrow$ Kapitel	$\downarrow$ Kapilel Erweiterte Regelkreisstrukturen	$\downarrow$ Kapitel	$\downarrow$ Kapitel	$\downarrow$ Kapitel

Geschichte der Regelungstechnik

Das Regelungsprinzip ist keine Erfindung des Menschen, sondern ein Naturphänomen!

• Beispiel Erdklima

Erdgeschichtlich gesehen, ist die globale Luft-Durchschnittstemperatur in Erdbodennähe (Meereshöhe) seit vielen millionen Jahren relativ konstant. Das Regelungsprinzip für den schmalen Temperaturbereich als Klima-Voraussetzung des höher entwickelten biologischen Lebens kommt in der Natur zur Anwendung, wenn z.B. durch eine steigende Lufttemperatur die globale Wasser-Oberflächentemperatur der Weltmeere steigt und durch Wasserdampf mit Wolkenbildung die Sonneneinstrahlung reduziert. Dabei greifen zahlreiche langfristige und kurzfristige Störgrößen zur Klimaveränderung ein:

• Langfristige Störgrößen:

Abstand Erde-Mond vergrößert sich (Gezeitenänderung), Meeresströme ändern ihre Richtung, Erdkontinentalplatten wandern (Kontinentaldrift), Erdmagnet-Pole wandern.

• Erdgeschichtlich kurzfristige Störgrößen:

Starker Vulkanismus führt zur Abkühlung, große Meteoriteneinschläge führen zu Abkühlung oder im Extremfall zur Erdoberflächenverbrennung, Perioden geringer Sonnenaktivitäten (Sonnenflecken) bewirken eine leichte Abkühlungen (Kleine Eiszeit umstritten!).

Biologisch: Algenwachstum und Eisendüngung (als Kohlenstoffbindung zur Kohlendioxyd-Reduzierung: umstritten!) , Abholzung der Wälder, Verbrennen fossiler Brennstoffe und erhöhter Methanausstoß (Siehe Alkane) führen zum Treibhauseffekt.

• Beispiel: Biologische Systeme und Geologie

Die Gaia-Hypothese wurde von der Mikrobiologin Lynn Margulis und dem Chemiker, Biophysiker und Mediziner James Lovelock Mitte der 1960er-Jahre entwickelt. Sie besagt, dass die Erde und ihre gesamte Biosphäre wie ein Lebewesen betrachtet werden kann.

• Beispiel: 'Regelungsvorgänge der lebenden Natur

Bei Tieren als Warmblüter: geregelte Körpertemperatur und geregelter Blutdruck, Pupillenöffnung reagiert auf Lichteinfall, aufrechter Gang bei Zweibeinern.

Das Hase-Fuchs-Population-Modell (siehe Räuber-Beute-Beziehung und Lotka-Volterra-Regeln) als Beispiel für das biologisches Gleichgewicht regelt eine Führungsgröße als Funktion der unterschiedlichen Nahrungsangebote auf eine annähernd feste Hase-Fuchs-Verhältniszahl.

Störgrößen: Veränderte Geländeeigenschaften, Klima, Krankheit, Mensch.

Tabelle der historischen Ereignisse der Regelungstechnik:

Jahr	Forscher Mathematiker	Historische Ereignisse der Regelungstechnik
300 v. C	Ktesibios aus Alexandria Schüler ?: Philon von Byzanz	Wasserkanäle, Kombinierte Saug- und Druckpumpe, Wasserorgel, Wasserstandsregler (siehe Schwimmschalter)
1. Jahrhundert	Heron von Alexandria	Heronsbrunnen Füllstandsregelung
ca. 1770	Leonhard Euler	Differential- und Integralrechnung u. a. mit Differenzengleichungen, Wegbereiter der numerischen Berechnung Eulersches Polygonzugverfahren, Euler-Gleichungen.
ca. 1780	Pierre-Simon Laplace	Systembeschreibungen mit Hilfe der Laplace-Transformation Laplace-Gleichung, Laplace-Operator.
1782	James Watt	Beginn der Industriellen Revolution Konstruktion einer Dampfmaschine
1788	James Watt	Fliehkraftregler für Windmühlen und Dampfmaschinen
1868	James Clerk Maxwell	Systembeschreibung verschiedener Regler durch Differentialgleichungen
1895	Adolf Hurwitz	Stabilitätskriterium in Abhängigkeit des Nennerpolynoms, Hurwitzpolynom
1922	Nicolas Minorsky	Schiffsteuerung mit PID-Regelung bei US-Navy
1932	Harry Nyquist	Stabilitätskriterium basierend auf der Ortskurve des Frequenzgangs
1938	Hendrik Wade Bode	Frequenzganganalyse (Bodediagramm)
1942	Ziegler / Nichols	Einstellregeln für P-, PI- und PID-Regler
1942	Norbert Wiener	Modelle der Prädiktion (Vorhersage) Modelle der Flugbahn von Flugzeugen Automatische Zielsteuerung 1947 Schöpfer des Begriffs "Kybernetik"
1948	Walter Richard Evans	Wurzelortskurve
1960	Rudolf Kálmán	Kalman-Filter, Zustandsraumdarstellung
1962	Richard Bellman	Optimalitätsprinzip von Bellman Dynamische Programmierung, Bellman-Algorithmus

Einführung

oben: Steuerung, Wirkungskette zwischen Führungsgröße und zu steuernder Größe
unten: Regelung, geschlossener Wirkungskreis

Aufgabe

Die Regelungstechnik behandelt und löst die Aufgabe, in technischen Systemen (Geräte, Apparate, Maschinen, Anlagen und biologische Systeme) vorkommende, prinzipiell veränderliche (dynamische) Größen automatisch konstant (oder gezielt veränderlich) zu halten, das heißt Störeinflüsse auszugleichen. Solche Regelgrößen sind meist physikalischer (zum Beispiel Temperatur, Druck, Drehzahl und vieles andere), selten chemischer (zum Beispiel pH-Wert im Abwasser) oder biologischer (zum Beispiel Glucose-Konzentration im Blut) Natur.

Grundprinzip

Das Grundprinzip besteht darin, den Wert der Regelgröße zu messen (Ist-Wert) und abhängig von seiner Abweichung zum Soll-Wert mittels der in der Regel bereits vorhandenen Möglichkeit seiner Beeinflussung (Steuerung) automatisch (mit dem Stellglied) korrigierend einzugreifen. Durch die Rückkopplung der Regelgröße über Messglied und Regler zur Steuergröße entsteht ein geschlossener Wirkungskreis (Regelkreis, siehe Abbildung). Der geschlossene Kreis ist das eindeutige Unterscheidungsmerkmal einer Regelung von einer Steuerung.

Die meisten Regelungen werden verwendet, um den Einfluss von Störungen, die innerhalb des Systems (Regelstrecke) stattfinden, zu kompensieren. Die Regelgröße soll den vorgegebenen festen Sollwert einhalten: Festwert- oder Störgrößenregelung.

Soll die Regelgröße zusätzlich gezielt verändert werden, so handelt es sich um eine Folge- oder Nachlaufregelung. Der variable Sollwert wird Führungsgröße genannt. Wenn keine Störungen zu kompensieren sind, kann die Führungsgröße lediglich die Eingangsgröße einer Steuerung sein.

Bei einer Steuerung gibt es anstatt eines geschlossenen Kreises nur eine Wirkungslinie: vom Eingang des Stellglieds zum Ausgang (zu steuerndende Größe) der Steuerstrecke. Ein Regelkreis entsteht daraus allenfalls dann, wenn eine bedienende Person die Aufgabe des Reglers übernimmt, wenn “von Hand geregelt” wird (sowohl mit fixem Sollwert als auch mit variabler Führungsgröße).

Ältestes technisches Beispiel ist die Regelung auf fixe Drehzahl einer Dampfmaschine durch James Watt mit Hilfe des Fliehkraftreglers (siehe Abbildung).

Praktische und theoretische Regelungstechnik

Regelungen befinden sich in vielen technischen Produkten und Prozessen. Es lassen sich Standard-Regler bauen, die grundsätzlich in verschiedensten Bereichen der Technik eingesetzt werden können. Ihr Einsatz ist aber ohne Kenntnis des dynamischen Verhaltens der technischen Systeme nur mit eingeschränktem Erfolg möglich. Am Anfang wurde die Anpassung durch Ausprobieren mit nicht sicherem und nicht optimalem Erfolg vorgenommen.

Besseren Erfolg hatte man, als es gelang, das im Wesentlichen von den Verzögerungen in der Regelstrecke bestimmte komplexe dynamische System Regelkreis mit Hilfe von Differentialgleichungen quantitativ zu beschreiben. Methoden zum Lösen der Differentialgleichungen waren zu erlernen. Die Regelungstechnik etablierte sich infolgedessen als eigenständige Disziplin der Ingenieurwissenschaften. Mathematiker, aber auch Regelungstechniker selbst fanden mathematische Formen der Darstellung, mit deren Hilfe die Leistungsfähigkeit eines Regler-Entwurfs theoretisch vorhersagbar oder eine Regelung optimierbar ist. Die Regelungstechnik ist wie ihr Untersuchungsgegenstand spartenübergreifend und verlangt von den in ihr Tätigen Wissen in der gesamten Technik, der Physik und vertiefte mathematische Kenntnisse.

Durch den Einbezug der in natürlichen Systemen vorhandenen Regelungen entstand in den 40er Jahren des 20. Jahrhunderts die noch breiter greifende Wissenschaft Kybernetik, deren Begründer Norbert Wiener war. Die moderne Theorie der Regelungen (oder der Regelungstechnik) hat sich als Kontrolltheorie formal zu einer mathematischen Disziplin gewandelt.

Geschichte

Ausgeführte Regelungen

Das Prinzip der Regelung wurde schon von Mechanikern in der Antike angewendet. Nachgewiesen sind Einrichtungen zur Regelung von Flüssigkeits-Niveaus, die Ktesibios aus Alexandria und sein Schüler Philon von Byzanz erfanden. Ktesibios regelte den Wasserstand in einem Behälter, aus dem eine Einlaufwasseruhr mit Wasser versorgt wurde.^[1][2] Der Wasserzufluß von konstanter Höhe herab ist gleichmäßig und erhöht die Genauigkeit der Uhr. Von Phylon ist eine Öllampe bekannt geworden (siehe Abbildung), in der das Öl automatisch auf gleichem Niveau gehalten wurde. Das konstante Ölniveau verbesserte den gleichmäßigen Brand der Flamme, ein Luxus, auf den man verzichten könnte und bei heutigen Öllampen auch verzichtet. Der Aufwand war aber klein, obwohl es sich um eine vollwertige Regelung handelte.

Danach wurde das Prinzip der Regelung erst wieder in der Neuzeit aufgegriffen. Im 17. Jahrhundert entstand die erste Temperaturregelung, die der Niederländer Cornelis Jacobszoon Drebbel in einem Brutkasten für Hühnereier entwarf.^[3] 1681 erfand der Franzose Denis Papin eine einfache Druckregelung für einen Dampfkochtopf durch Einbau eines Überdruckventils.

Der erste in Serie hergestellte Regler war der Fliehkraftregler, dessen Erfindung James Watt fälschlicherweise zugeschrieben wird (siehe Abbildung, oben). Der Fliehkraftregler wurde vorher schon an Windmühlen verwendet. Watt hat die 1769 von Thomas Newcomen erfundene Dampfmaschine im Jahr 1786 mit einem solchen Regler ausgerüstet. Für die neue Dampftechnik kam auch die aus der Antike bekannte Wasserstandsregelung mit Schwimmer durch den Russen Ivan Polzunov zur Anwendung. Der Schwimmer beeinflusste über ein Gestänge das Wasser-Einlassventil des Dampfkessels.

Die Technik der selbsttätigen Regelung blieb lange Zeit auf die Anwendung in Kraftmaschinen beschränkt. Eine erste Ausweitung erstreckte sich auf die Regelung von Größen in verfahrenstechnischen Prozessen, vor allem von Temperaturen, Drücken und Massenströmen. Nach dem zweiten Weltkrieg entstanden die vereinheitlichten, vielfach einstellbaren elektrischen, hydraulischen und pneumatischen PID-Regler. Die pneumatischen PID-Regler werden in der Verfahrenstechnik bevorzugt, da von ihrer Hilfsenergiequelle Luftdruck keine Brandgefahr ausgeht.

In der jüngsten Vergangenheit hat sich die Anwendung der Regelungstechnik auf alle Gebiete der Technik ausgedehnt. Anstöße gaben die Ausweitung der Automatisierung, zum Beispiel mit Hilfe von Robotern, und die neue Weltraumtechnik. Die Regelungstechnik ist inzwischen eine Symbiose mit der Informationstechnik (sowohl Hard- als auch Software) eingegangen.

Theorie der Regelungstechnik

Die quantitative (mathematische) Beschreibung der einzelnen dynamischen Elemente und ihres Zusammenschlusses im Regelkreis wird benötigt, um eine Regelung optimal auslegen zu können. Alle Elemente, vor allem die Regelstrecke, verzögern die Wirkung zwischen ihrem Eingang und ihrem Ausgang, weshalb jede Regelung infolge der Rückführung prinzipiell unstabil sein kann, und die Regelgröße fortwährend zwischen ihrem maximal möglichen und ihrem minimal möglichen Wert schwankt. Die Regelung ist optimal, wenn eine Regelabweichung möglichst schnell beseitigt wird, ohne dass unstabiles Schwingen entsteht.

Die mathematische (theoretische) Behandlung der Regelungstechnik begann bereits anhand der Drehzahlreglung mit Fliehkraftregler. Am Ende des 19. Jahrhunderts beschrieben Maxwell und der russische Ingenieur Wischnegradsky erstmalig solche dynamischen Systeme mit Differentialgleichungen.^[4] Damit war der Grundstein für die eigenständige Disziplin Regelungstechnik gelegt. Schon kurz danach, am Anfang des 20. Jahrhunderts, bediente man sich auch für Technische Systeme der allgemeinen Laplacetransformation^[4] und ihrer inversen Rücktransformation zwischen Zeitbereich und Frequenzbereich, um den großen Rechenaufwand für direktes Lösen der Differentialgleichungen zu vermeiden. Im Frequenzbereich bestehen leicht lösbare gewöhnliche algebraische Gleichungen.

Die Anwendung der speziellen Fouriertransformation auf die Differentialgleichungen führt zum Frequenzgang, der schon vorher in der Nachrichtentechnik verwendet wurde, um die Übertragung ungedämpfter elektromagnetischer Schwingungen zu beschreiben.^[4] Er wird als Bode-Diagramm oder als Ortskurve dargestellt. Etwa 1928 erkannte Nyquist, dass aus der Ortskurve des Frequenzgangs des aufgeschnittenen Kreises eines elektronischen Verstärkers oder einer Regelanalage ein Stabilitätskriterium für den geschlossenen Kreis entnommen werden kann.^[5] Die Kurve muss einen bestimmten Verlauf nehmen.

Die mit der Laplacetransformation erhältliche Übertragungsfunktion wurde für das Wurzelortskurvenverfahren (root locus method ^[6]) bedeutsam. Mit dem Frequenzgangverfahren und diesem Verfahren als zweite allgemeine Methode zur Beschreibung und Bearbeitung linearer Regelungen ^[7] waren im Wesentlichen alle mathematischen Hilfen gefunden, die zur Behandlung linearer zeitinvarianter Regelungssysteme verwendet werden können.

Die folgende erhebliche Ausweitung der Regelungstechnik bezog nichtlineare Systeme und Regelkreise mit mehreren Regelgrößen und mehreren Schleifen ein. Neue Güte-Kriterien mussten erfüllt werden, zum Beispiel die Bahnoptimierung bezüglich Zeit und Treibstoffverbrauch in der Raumfahrt.^[4] Entsprechende und zahlreiche neue mathematische Hilfsmittel wurden gefunden. Die sogenannte moderne Regelungstheorie, zu deren Entwicklung Kálmán maßgeblich beitrug,^[8] begann in den 70er Jahren des letzten Jahrhunderts. Durch Anwendung des Modells Zustandsraum lassen sich die Systeme hier auch im Zeitbereich mit erträglichem Aufwand behandeln.

Mit der modernen Regelungstheorie begann eine verallgemeinerte, das heißt eine mehr mathematisch betonte Betrachtung, deren Bindung an die Regelungstechnik lockerer wurde. Es entstand die Kontrolltheorie als mathematische Disziplin. Ihre Verallgemeinerung und entsprechende Einordnung ist noch undeutlich. In der Literatur wird sie noch vorwiegend als Theorie der Regelung (oder der Regelungstechnik) bezeichnet. Die neuen mathematischen Mittel zur Beschreibung und theoretischen Behandlung werden mit entsprechenden technischen Entwürfen sehr hoher Komplexität und schwierigen Bedingungen (keine Linearität, keine Invarianz und ähnlichem) zunächst veranschaulicht. Die erfolgreiche Erprobung geschieht parallel dazu. Die Mehrzahl installierter Regelungen kann aber mit den bisherigen Methoden behandelt werden. Sie sind oft mit dem standardisierten PID-Regler ausgerüstet.

Bis zum Ende des 2. Weltkrieges entwickelten sich Theorie und Praxis der Regelungssysteme in den USA und Westeuropa anders als in Russland. Während im Westen die Theorie rückgekoppelter Systeme vorwiegend im Frequenzbereich, vor allem von Bode und Nyquist, entwickelt wurde, entstanden in der ehemaligen UdSSR durch die Nachfolger von Wischnegradsky verbesserte Lösungen im Zeitbereich. Die Trennung in Ost und West wurde wenigstens außerhalb militärischer und Weltraum-technischer Anwendungen nach dem 2. Weltkrieg beendet. Im September 1956 wurde die International Federation of Automatic Control (IFAC) gegründet.

In den 80er Jahren erfuhr die Regelungstechnik mit der Einführung des digitalen Rechners einen erneuten Entwicklungsschub. Dieses neue Werkzeug ermöglichte es, wesentlich größere und komplexere mathematische Modelle des Regelkreises als bisher in kurzer Zeit zu überblicken. Seitdem entstanden entsprechend komplexere und präzisere Regelungen.

Lehre und Forschung in Regelungstechnik an einer Universität begannen erst in den 40er Jahren des vorigen Jahrhunderts. Nyquist, Bode und die anderen frühen Förderer wirkten alle in der Industrie. Das erste Institut für Regelungstechnik im deutsch-sprachigen Raum wurde 1955 von Heinrich Kindler an der Technischen Hochschule Dresden (TH Dresden, später TU Dresden) gegründet.^[9]

Einfache Beispiele einer Regelung

Das Grundprinzip beim Regeln ist allgemein gültig. Es ist nicht an die reale Ausprägung der Regelstrecke und der dieser zum Regeln zugefügten Funktionselemente gebunden. Der Regelkreis kann abstrakt als Blockschaltbild dargestellt werden, in dem nur die Funktionselemente als Kästchen und die Funktionsgrößen als Linien erscheinen, die die Kästchen verbinden.

Ein einfaches, anschauliches Beispiel für eine Standard-Regelung ist die bereits oben abgebildete, von James Watt verwendete Drehzahlregelung an einer Dampfmaschine.

Einfache Raumtemperatur-Regelung

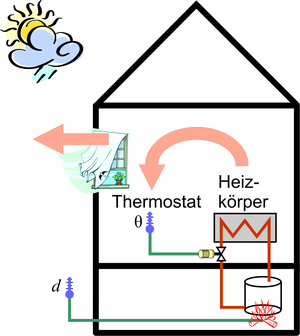
Die Regelung einer Raumtemperatur mit Hilfe eines an einem Heizkörper angebrachten Thermostatventils ist ebenfalls ein einfaches, anschauliches Beispiel einer einfachen Regelung. Ziel ist das automatische Halten der Raumtemperatur (Regelgröße) auf einem gewünschten Wert (Sollwert), obwohl durch gelegentliches Öffnen der Fenster und Änderungen der Außentemperatur eine variable Wärmemenge aus dem Raum abgeführt wird.

Ein Thermostatventil ist entgegen seiner umgangssprachlichen Bezeichnung mehr als ein Ventil. Es ist Messglied, Regler und Stellglied zugleich. An ihm wird die gewünschte Solltemperatur (Sollwert) des Raumes eingestellt. Das Ventil verändert den Warmwasserstrom durch den Heizkörper und damit die Raumtemperatur. Die Flüssigkeit im Sensor (Dehnstoffelement) dehnt sich bei Erwärmung aus und stellt einen veränderten Istwert dar. Durch diese Dehnung wird die Ventilöffnung direkt verkleinert, wodurch sich der Warmwasserstrom durch den Heizkörper verringert. Nach einer Verzögerung sinkt die Temperatur im Raum.

Regelung der Raumtemperatur θ mit Thermostatventil am Heizkörper

Bezeichnung	Zeichen im Beispiel	Zeichen nach DIN	Bedeutung im Beispiel (Raumtemperatur-Regelung mit Thermostatventil)
Regelstrecke			Zimmer und Heizkörper
Störgrößen	d	z	Außentemperatur, Fenster-Stellung (geschlossen bis offen) und anderes
Regelgröße	y	x	Raumtemperatur
Messglied			Dehnstoffelement im Thermostatventil
Messgröße	yM	yM	Ausdehnung des Dehnstoffelementes
Istwert der Regelgröße			zum Beispiel 22 °C, dem eine bestimmte Ausdehnung des Dehnstoffelementes entspricht
Führungsgröße	w	w	Position des Bodens des Dehnstoffelementes, die mit Drehknopf (mit °C skalierter Skala) am Thermostatventil eingestellt wird
Sollwert der Regelgröße			zum Beispiel 20 °C, zur entsprechenden Ausdehnung des Dehnstoffelementes gehört die entsprechend eingestellte Position seines Bodens
Regelabweichung	e = w − y	e = w − x	z. B. 2K
Regler			Dehnstoffelement
Steuergröße	u	y	Position des Übertragungsstiftes am Dehnstoffelement (Übertragung auf das Ventil)
Stellglied			Ventil im Thermostatventil
Stellgröße	uR	uR	Stellung des Ventils (geschlossen bis offen)

Blockschaltbild eines Standardregelkreises

Raumtemperatur-Regelung mit Störgrößenaufschaltung

Die Regelung der Raumtemperatur wirkt besser, wenn zum Beispiel ein Absinken der Außentemperatur bereits durch Erhöhen der Vorlauftemperatur des Warmwassers berücksichtigt wird. Diese verbesserte Regelung kompensiert das Absinken schneller, als wenn sie erst die Änderung der Zimmertemperatur abwarten würde. Sie ist auch wirksamer, weil sie durch Veränderung der Vorlauftemperatur eine zusätzliche Stellgröße benutzt. Eine solche Maßnahme heißt Störgrößenaufschaltung, die möglich ist, wenn eine Störgröße (im Beispiel die Außentemperatur) bekannt und messbar ist. Die Kenntnis des dynamischen Zusammenhangs zwischen dieser Störgröße und der Regelgröße ist ebenfalls nötig.

Schritte beim Lösen einer Regelungs-Aufgabe

Die folgende Aufstellung enthält Einzelschritte, die bei der Entstehung einer Regelung prinzipiell gemacht werden.^[10] Die Reihenfolge ist weniger streng. Die Schritte zwischen Aufgabenstellung und Inbetriebnahme werden unter Anwendung inzwischen vorliegender Ergebnisse meistens wiederholt vorgenommen.

• Formulierung der Aufgabe: Oftmals ist die zu lösende Regelungs-Aufgabe Teil eines größeren Automatisierungsvorhabens. Aus diesem ist die Einzelaufgabe herauszulösen, Randbedingungen durch die Einbettung aber zu erkennen. Anforderungen an Genauigkeit, Geschwindigkeit und anderes sind zu übernehmen oder zu formulieren.
• Wahl eines Stellgliedes und einer Messeinrichtung: Im zu regelnden System findet meistens ein Energie- oder/und Masse-Fluss statt, für dessen Beeinflussung ein entsprechendes Stellglied schon vorhanden oder vorgegeben ist. Beispielsweise wird die Wärme/Wasser-Menge bei einer Raumheizung mittels Ventilen an den Radiatoren verändert - sowohl ohne als auch mit automatischer Regelung der Raumtemperatur. Ist das vorgegebene dynamische System aber neu, kann sich die Frage stellen, wie es beeinflussbar ist und wie die Regelgröße gemessen werden kann.

Auf die weiteren Einzelschritte wird anschließend tiefer eingegangen. Die Beschreibung ist beispielhaft für einfache Regelungen, bei der nur eine Regelgröße, nur ein Regelkreis und nur ein Stellglied vorhanden sind. Ein weiteres Kriterium für Einfachheit ist die Zeitinvarianz des betroffenen Systems, was heißt, dass es sein Verhalten über lange Zeit nicht ändert. Die Nennung der verwendeten mathematischen Werkzeuge steht im Vordergrund, die Durchführung der mathematischen Arbeit wird aber nur angedeutet.

• Beschreibung des Systems und der zum Regeln gebrauchten Teile, Analyse
• Entwurf der Regelung, Synthese
• Korrektur der dynamischen Eigenschaften der Regelung
• Prüfung des Ergebnisses durch Simulation
• Bau und Inbetriebnahme der Regelung

Eigenschaften des Systems und der zum Regeln gebrauchten Teile

Um eine Regelung zu erstellen, ist die möglichst gute Kenntnis aller beteiligten Teile im Regelkreis erforderlich. Sich diese Kenntnis zu verschaffen und sie in mathematischer Sprache auszudrücken, wird in der regelungstechnischen Literatur oft - aber nicht generell - unter dem Begriff Regelungs-Analyse zusammengefasst. Der Gebrauch dieses Begriffs schließt alle Teile ein, obwohl wenigstens über den gewählten Regler ausreichende Kenntnis vorhanden ist. Die Untersuchung zum Zwecke der Verbesserung einer entworfenen oder vorhandenen Regelung wird in der regelungstechnischen Literatur auch oft - aber auch nicht generell - als Analyse bezeichnet (siehe weiter unten: Analyse des Regelkreises).

Mathematische Beschreibung: Differentialgleichungen und Linearität

Dynamische Systeme sind verbal sehr ungenügend zu beschreiben. Ihre Größen sind Funktionen der Zeit, denen sich nur in mathematischer Beschreibung folgen lässt, wie es in der Systemtheorie geschieht. Für ein dynamisches System ist anzugeben, wie sich eine Größe durch den Einfluss einer anderen Größe zeitverzögert verändert. Der dafür verwendbare Teil der mathematischen Sprache sind die Differentialgleichungen.

Die Übertragungsfunktion in einem linearen System (Abhängigkeit einer Ausgangsgröße von einer Eingangsgröße ^[11]), kann auf einfache Weise mit einer linearen gewöhnlichen Differentialgleichung angegeben werden. Die Linearität des Systems (der Regelstrecke) ist Kennzeichen der einfachen, klassischen Regelungstechnik. Bei Verwendung digitaler Regler (älterer Ausdruck Abtastregler) werden Differenzengleichungen anstatt Differentialgleichungen benutzt. Solche Regler sind zeitdiskrete Systeme im Gegensatz zu den häufigeren zeitkontinuierlichen Systemen.

Nichtlinearität bedeutet, dass die mathematische Beschreibung weniger einfach ist. Wenn die Regelstrecke nichtlineares Verhalten aufweist, kann man sich behelfen, indem man den benutzten Teil der Übertragungsfunktion näherungsweise als linear ansieht. Die Beschreibung nichtlinearer Regelstrecken erfolgt prinzipiell mit nichtlinearen Differentialgleichungen, die nur mit höherem Aufwand lösbar sind.

Mathematisches Modell der Regelstrecke

Von den im Regelkreis enthaltenen Teilen ist die Regelstrecke das am stärksten dynamisch geprägte System. Seine Abbildung in einem mathematischen Modell gilt beispielhaft für alle anderen Teile im Regelkreis.

Modell ist ein anderes Wort für die Beschreibung einer Realität. Es wird in der Regelungstechnik häufig gebraucht, wobei meistens die mathematische Beschreibung gemeint ist. Es ist wie jede Beschreibung eine Näherung an die Realität, hier an das dynamische Verhalten der Regelstrecke.

Die im Modell der Regelstrecke veränderlichen Größen werden formal nicht als physikalische, chemische oder andere reale Größen sondern nur als Eingangs-, Stör- oder Ausgangsgrößen behandelt. Der reale Charakter tritt in der Rechenphase, in der man sie zur einfacheren Handhabung (auf ihre Dimensionen muss nicht geachtet werden) als relative, auf ihre mittleren Funktionswerte bezogene Größen benutzt, nicht in Erscheinung. Ungeachtet dessen muss das Modell natürlich die Abhängigkeit der Ausgangs- von der Eingangsgröße in möglichst guter Näherung an die der realen Größen beschreiben.

Wenn die Regelstrecke bereits existiert (und für Untersuchungen zur Verfügung steht), kann das Übertragungsverhalten experimentell ermittelt werden. Die Eingangsgröße wird entweder sprungartig oder sinusförmig verändert und der Verlauf der Ausgangsgröße aufgezeichnet. Wenn eine Störgröße herausstellbar ist und gezielt verändert werden kann, wird das Übertragungsverhalten zwischen ihr und der Ausgangsgröße ebenfalls aufgenommen, wodurch die Regelstrecke insgesamt besser erfasst wird. Den Experimenten schließt sich das Aufstellen der mathematischen Gleichungen an, wobei Vereinfachungen vorgenommen werden müssen, um zu einem beherrschbaren Satz von Gleichungen zu kommen. Dies auf Experimenten beruhende, sogenannte experimentelle Modellierung hat auch die Bezeichnungen White-Box-Modellierung und strukturelle Modellbildung.

Das andere Extrem ist die theoretische Modellbildung. Hierbei werden die Gleichungen allein durch Anwendung der physikalischen Gesetze auf die Vorgänge in der Regelstrecke entwickelt, weil die Regelstrecke experimentell nicht zugänglich ist oder noch nicht existiert. Das gewonnene Modell ist weniger sicher, sowohl prinzipiell als auch quantitativ (Übertragungsfaktoren und Zeitkonstanten). Andere Bezeichnung des Vorgangs sind Black-Box-Modellierung und pragmatische Modellbildung.

Mit Grey-Box-Modellierung wird ausgedrückt, dass Ergebnisse aus Experimenten und aus theoretischen physikalischen Überlegungen zu einem Modell führen.

Mathematische Modelle der zum Regeln gebrauchten Teile

Bei Stellgliedern ist es oft nicht leicht, lineares Verhalten zu erreichen. Hingegen ist das Messglied meistens unproblematisch. Sein Modell ist lediglich eine lineare Funktion (P-Glied), zeitliche Verzögerungen sind in der Regel vernachlässigbar.

Der Regler selbst wird als dynamisches System so gestaltet, dass die Regelaufgabe - wie gewollt und wie unter den vorhandenen physikalischen Bedingungen möglich - erfüllt wird. Ein klassischer Regler ist der PID-Regler, in dem drei der elementaren Übertragungsglieder einstellbar enthalten sind: Proportionalglied (P-Glied), Integralglied (I-Glied) und Differentialglied (D-Glied).

Elementare Übertragungsglieder

Die drei im PID-Regler enthaltenen Übertragungsglieder ergeben zusammen mit den beiden Verzögerungsgliedern PT₁ und PT₂ und dem Totzeitglied PT_t die sechs elementaren Übertragungsglieder, die in vielfältiger Kombination auch die Regelstrecke beschreiben. In der Regelstrecke überwiegt Proportionalität in Kombination mit Zeitverzögerung (PT-Glieder), Integration (I-Glied) kommt öfters, Differentiation (D-Glied) aber kaum vor.

Es ist üblich, elementare Übertragungsglieder mit der graphischen Darstellung der Sprungantwort^[12] symbolisch zu kennzeichnen. Diese Symbole werden in die entsprechenden Übertragungs-Blöcke ausführlicher Blockschaltbilder (ausführlicher als im Prinzip-Blockschaltbild des Regelkreises) eingetragen.

Entwurf einer Regelung

Hauptartikel: Regler

Der Entwurf einer Reglung - die Verbindung eines Reglers mit der Regelstrecke zu einem geschlossenen Kreis - ist die eigentliche Aufgabe der Regelungstechnik. In der regelungstechnischen Literatur wird für diesen Prozess oft, aber nicht generell der Begriff Regelungs-Synthese gebraucht.

Gute Kenntnis des dynamischen Verhaltens aller Teile des Kreises kann bereits zu einem ausreichenden Ergebnis führen. Da die Kenntnisse aber oft lückenhaft sind, und weil die Anforderungen an die Güte einer Regelung für den Entwurf zum Teil konträre Bedingungen darstellen, ist der Entwurf nicht eine einfache und einmalige Synthese. Mit Kriterien der Stabilität des Kreises und einer möglichst hohen Güte, mit der die Regelgröße kontrolliert wird, schließen sich in der Regel weitere theoretische Schritte an, die sowohl Synthese, aber auch Analyse (des Verhaltens im Kreis) sind. Theoretisch entworfene Regelungen werden oft anhand eines (elektronischen) Modells überprüft. Letztlich müssen Nachbesserungen bei der Inbetriebnahme vorgenommen werden.

Angegeben wird nur eine Übersicht der Entwurfs-Verfahren.

Konträre Anforderungen

Mit einer Regelung ist das Stabilitätsproblem untrennbar verbunden. Es ist der Preis, den man dafür bezahlen muss, dass eine Regelung mehr kann als eine Steuerung, nämlich ein in nicht genauer Weise veränderliches System gezielt zu beeinflussen.^[13] In einem geschlossenen Wirkkreis können die Größen prinzipiell um einen mittleren Wert hin- und herpendeln. Ursache sind die so gut wie immer vorhandenen Übertragungsglieder mit Zeitverzögerung. Eine Regelung ist stabil, wenn entstehende Schwingungen abklingen und mit der Zeit verschwinden, sie ist dann im mindesten Maße gedämpft, die Verstärkung im Regler (P-Glied) ist nicht zu hoch eingestellt.

Vorhandene Stabilität heißt allein nicht, dass die anfängliche Schwingweite (Überschwingen nach einer Störung) innerhalb der Anforderungen liegt.

Konträr zum Erfolg, den man mit einer bestimmten Dämpfung erreicht, ist die Forderung, dass eine Regelung schnell sein soll. Bei notwendig hoher Dämpfung kann es vorkommen, dass der Sollwert nach einer Störung nur kriechend wieder erreicht wird, was mit den Anforderungen nicht vereinbar sein kann.

Verlangt wird auch eine genügende stationäre Genauigkeit: Die nach dem Abklingen des Einschwingvorganges sich einstellende Differenz zwischen Soll- und Istwert der Regelgröße soll unterhalb eines Grenzwertes liegen.

Die mathematische Behandlung ist nur mit erhöhtem Aufwand möglich, wenn der Arbeitsbereich des realen Systems verlassen wird. Es ist beispielsweise sinnvoll, darauf zu achten, dass beim Regeln nicht Stellgrößen-Werte jenseits von “ganz offen” erwartet werden.

Die Stabilität des Regelkreises ist unbedingt zu gewährleisten. Bei der mathematischen Behandlung werden verschiedene Stabilitätskriterien angewendet, mit denen sich eine Auslegung der Regelung finden lässt, die vermutlich stabil ist.

Die zueinander konträren Anforderungen müssen in der Regel in einer Kompromiss-Lösung beschnitten werden. Sie sind Gegenstand von verschiedenen Gütekriterien, mit deren Hilfe ihre quantitative Benennung möglich ist.

Heuristische Einstellregeln für einfache Regelungen

Hauptartikel: Faustformelverfahren (Automatisierungstechnik)

In der Mitte des 20. Jahrhunderts begann die serienmäßige Herstellung von PID-Reglern und damit eine Standardisierung für die Ausführung von Regelungen mittlerer Schwierigkeit und Güte. Mit PID-Reglern und Anwendung der dafür erarbeiteten Regeln für die Einstellung ihrer Parameter (Verstärkung und Zeitkonstanten) lassen sich auch heute noch die meisten Regelungen verwirklichen. Die anspruchsvolle Modellbildung und die mathematische Behandlung sind schwierigeren Regelstrecken und Fällen mit hoher Güte-Anforderung vorbehalten.

Die Anwendung der Faustformelverfahren genannten Einstellregeln ist eine heuristische (dennoch systematische) Methode zum Auslegen einer stabilen und nicht zu langsamen Regelung. Die verschiedenen Verfahren unterscheiden sich hinsichtlich der Grundannahmen, die bezüglich der zu regelnden Strecke getroffen werden. Es müssen nur einige wenige Kennwerte der Regelstrecke, die aus einfachen Versuchen ermittelt werden können, bekannt sein.

Das Verfahren nach Ziegler und Nichols ist für stark verzögernde Regelstrecken, wie sie z. B. in der Verfahrenstechnik auftreten, gut geeignet. Die Einstellregeln nach Chien, Hrones und Reswick sind eine Weiterentwicklung dieses Verfahrens. Die T-Summen-Regel ist für Regelstrecken mit Tiefpassverhalten besser geeignet.

Linearer Entwurf

Von Entwurf wird gesprochen, wenn eine Regelung nicht einfach mit PID-Regler und einfachen Einstellregeln verwirklicht werden kann. Er ist linear, wenn alle im nötigen mathematischen Systemmodell enthaltenen Zusammenhänge linear sind. Das Modell beruht auf Annahmen und Näherungen, die bezüglich der realen Teile im Regelkreis (vor allem der Regelstrecke) vorgenommen werden. Deshalb ist die damit erreichte Güte theoretisch garantiert, aber nur beschränkt auf die Praxis übertragbar. Sie wird in der Praxis gut erreicht, wenn nur geringe Abweichungen vom Arbeitspunkt auftreten.

Die linearen mathematischen Modelle und ihre Lösungs-Methoden sind für zeitkontinuierliche und für zeitdiskrete Regelungen mehrheitlich verschieden.

Entwurf zeitkontinuierlicher Regelungen

Es existieren zahlreiche Entwurfsverfahren, von denen im Folgenden eine Auswahl angegeben wird. In der Regel ist keines der bekannten Verfahren vollständig. Während eines erfolgreichen Entwurfs werden oft mehrere Verfahren kombiniert oder nacheinander angewendet.

• Das Frequenzkennlinienverfahren ist das klassische Entwurfsverfahren. Es wurde in den 30er Jahren des 20. Jahrhunderts von Hendrik Wade Bode ausgearbeitet.^[14] Die Differentialgleichungen werden im Frequenzbereich gelöst. Dieser Umweg erleichtert nicht nur ihre Lösung. Das Übertragungsverhalten ist auch aus den Darstellungen im Frequenzbereich besser erkennbar. Die Darstellungen sind die Ortskurve des Frequenzgangs und die Frequenzgangkennlinien im Bode-Diagramm. Beispielsweise wird wie folgt verfahren: Ausgehend von den Dynamikforderungen an den geschlossenen Regelkreis werden Bedingungen an die Frequenzgangkennlinien der offenen Kette aufgestellt, die durch eine geeignete Wahl des Reglers erfüllt werden müssen.^[15] Die Stabilität wird mit dem Nyquist-Kriterium untersucht.^[16]

• Beim Wurzelortskurvenverfahren werden die Differentialgleichungen auch im Frequenzbereich gelöst. Es eignet sich nicht bei Regelstrecken mit Totzeit, ist aber mit Vorteil bei prinzipiell instabilen Regelstrecken anwendbar. Zusätzliche Untersuchungen , zum Beispiel mit dem Nyquist-Kriterium sind nicht erforderlich.^[17] Untersucht wird die offene Kette. Ihre zielgerichtete Veränderung - das heist des Verstärkungsfaktors des Reglers - erfüllt die Güteforderungen, die an den geschlossenen Kreis gestellt werden.^[18]

Beide bisher genannten Verfahren sind nicht streng systematisch, es sind typische Ingenieurmethoden, nämlich zielgerichtete Probierverfahren.^[19]

• Die Optimalregler-Verfahren verwenden mathematische Optimierungstheorie, um den Regler so zu bestimmen, dass ein Gütekriterium an die Bewegung des Ausganges und die erforderliche Stellenergie erfüllt ist. Das Verfahren ist für Mehrgrößensysteme geeignet. Dazu wird als Gütekriterium ein Funktional formuliert, in das der Regelfehler und die Stellgröße eingehen. Ziel der Optimierung ist die Minimierung des Gütefunktionals, so dass der integrale Regelfehler und die erforderliche Stellenergie minimal sind. Die Gewichtung von Regelfehler und Stellenergie kann durch Wichtungsmatrizen beeinflusst werden. Häufig wird ein quadratisches Gütekriterium verwendet, man spricht dann von einem LQ-Regler (von engl. linear quadratic regulator). Da zum Entwurf eine Riccatigleichung bzw. -differentialgleichung zu lösen ist, ist auch der Begriff Riccatiregler gebräuchlich.

• Beim Reglerentwurf zur Polvorgabe (engl. pole placement) geht man typischerweise von einer Darstellung im Zustandsraum aus. Die Güteforderungen aus dem Zeitbereich werden in die Lage der Eigenwerte übersetzt. Dann werden die Reglerparameter so bestimmt, dass die Eigenwerte des Regelkreises durch eine statische Rückführung die gewünschten Werte annehmen. Für Eingrößensysteme existieren unter üblicherweise vorhandenen Voraussetzungen (Steuerbarkeit) eindeutige Lösungen. Für ein Mehrgrößensysteme existieren üblicherweise unendlich viele Lösungen.^[20] Verfahren wie Modale Regelung^[20] oder die Entkopplung nach Falb-Wolowich^[21] schaffen Zusatzbedingungen, so dass wieder eindeutige Lösungen angegeben werden können. Falls die Strecke nicht steuerbar ist, gibt es einzelne feste Eigenwerte, die nicht verändert werden können.

• Die Zustandsrückführung erfordert die Kenntnis des Zustandes zu jedem Zeitpunkt. Unter bestimmten Voraussetzungen kann eine Zustandsrückführung durch eine Ausgangsrückführung ersetzt werden, ohne die Lage der erreichten Eigenwerte zu verändern. Ist die Regelstrecke beobachtbar, so kann der Zustandsvektor durch Einsatz eines Beobachters aus den Ausgangsgrößen rekonstruiert werden. Das Separationstheorem sichert dabei, dass (bei korrekter Streckenbeschreibung) Beobachterpole zu den Reglerpolen hinzutreten, diese aber nicht verschieben. Damit ist ein entkoppelter Entwurf von Regler und Beobachter möglich.

• In der robusten Regelung steht die Tatsache im Vordergrund, dass das mathematische Modell der Regelstrecke nur eine vereinfachte Näherung der realen Regelstrecke ist. In der robusten Regelung werden Regelungsverfahren entwickelt, die trotz Modellunsicherheiten die Stabilität (robuste Stabilität) bzw. eine Mindestgüte garantieren. Die Garantie gilt unter der Voraussetzung, dass der Modellfehler innerhalb einer analytischen Grenze bleibt.

Zeitdiskrete Regelung

In der zeitdiskreten Regelung, auch digitale Regelung oder Abtastregelung genannt, werden die Regelgröße und die Sollgröße in festen, gleichmäßigen Zeitabständen abgetastet und in digitale Zahlenwerte umgewandelt, also quantisiert. Der Regler berechnet aus diesen quantisierten Größen in jedem Zeitschritt die Stellgröße, die zum Abtastzeitpunkt ausgegeben und in ein Analogsignal umgewandelt wird. Ein Halteglied sichert, dass der Stellwert während des gesamten Zeitintervalls bis zum nächsten Abtastschritt anliegt. Die Quantisierung der Größen führt außerdem auf ein wertediskretes Signal. In der Regel wird die Quantisierung jedoch so fein gewählt, dass die Auswirkungen auf die Kreisdynamik vernachlässigt werden können.

Eine Vorgehensweise zum Entwurf zeitdiskreter Regler ist der Entwurf eines zeitkontinuierlichen Reglers und seiner Approximation durch einen zeitdiskreten Regler. Als Kriterium zur Approximation kann der Differentialquotient, das Integral oder das Pol/Nullstellen-Bild dienen. Diese Herangehensweise funktioniert besonders gut bei starker Überabtastung der Regelstrecke (z. B. das 20-fache der Grenzfrequenz).

Die meisten Prinzipien und Entwurfsverfahren der zeitkontinuierlichen Regelung haben eine sinngemäße Entsprechung in der zeitdiskreten Regelung. Zur mathematischen Behandlung von Abtastregelungen im Frequenzbereich wird dabei die z-Transformation eingesetzt.

Das Wurzelortskurvenverfahren hat eine direkte Entsprechung im zeitdiskreten Bereich, ebenso der Optimalreglerentwurf (LQ-Regler).

Zur Polzuweisung für zeitkontinuierliche Systeme existiert ein sinngemäßes Verfahren für zeitdiskrete Systeme.

Eine Besonderheit ist der Regler mit endlicher Einstellzeit, der es ermöglicht, den Sollwert nach einer endlichen Zahl n von Zeitschritten zu erreichen. Dabei ist n die dynamische Ordnung der Regelstrecke. Dieses verblüffende Ergebnis ist mathematisch durch das Cayley-Hamilton Theorem begründet.

Nichtlinearer Reglerentwurf

Die Methode der harmonischen Balance ist eine Methode zur Analyse nichtlinearer Regelkreise. Sie nutzt eine Beschreibung der nichtlinearen offenen Kette im Frequenzbereich, die auf der Beschreibungsfunktion der offenen Kette beruht. Dabei wird angenommen, dass die nichtlineare offene Kette aus der Reihenschaltung eines linearen und eines nichtlinearen Systems besteht. Die Beschreibungsfunktion hat eine zum Frequenzgang linearer Systeme analoge Bedeutung. Sie gibt an, wie harmonische Schwingungen übertragen werden. Auf Basis dieser Beschreibungsform kann ein Reglerentwurf,^[22][23] durchgeführt werden, obwohl die Methode der harmonischen Balance keine Synthesemethode ist.

Die Methode der globalen Linearisierung,^[24][23] (auch differentialgeometrische Methode oder exakte Linearisierung genannt) basiert auf der Idee, die Nichtlinearität in der Regelstrecke durch geeignete Vorfilter und Rückführungen zu kompensieren. Anschließend wird für das linearisierte System anhand linearer Reglerentwurfsmethoden das dynamische Verhalten an die Güteforderungen angepasst. Der nichtlineare Entwurf wird somit auf linearen Entwurf zurückgeführt.

Die Flachheitsbasierte Regelung ^[25][26] stützt sich auf den Begriff der Flachheit (engl. flatness), der eine Erweiterung des Begriffs der Steuerbarkeit für nichtlineare Systeme ist. Er erlaubt den systematischen Entwurf von Vorsteuerungen für flache nichtlineare Systeme durch Systeminversion. Meist wird die Steuerung durch eine Regelung zur Störunterdrückung ergänzt.

Die Idee des Gain scheduling basiert auf der Annahme, dass das nichtlineare System in jedem Betriebspunkt linearisiert werden kann. Für jeden Betriebspunkt wird ein Regler fester Struktur entworfen, dessen Parameter vom Betriebspunkt abhängen. Bei der Realisierung werden die Parameter in Abhängigkeit vom Betriebspunkt eingestellt. Eine spezielle Klasse nichtlinearer System, sind lineare Systeme, deren Systemmatrizen explizit von Parametern θ abhängen. Diese Systeme werden als linear parameter-varying (LPV) Systeme bezeichnet. Im LPV-gain scheduling werden die Reglerparameter explizit von θ abhängig gemacht.

Ein nichtlineares Regelungsverfahren, das mit schaltenden Reglern arbeitet, ist Sliding mode control.

Weitergehende Regelungskonzepte

In zahlreichen Anwendungsgebieten (z. B. Flugregelung) bleibt die Struktur des Modells über den gesamten Arbeitsbereich gültig, es ändern sich jedoch einzelne Parameter. Beispiele sind die Änderung der Dichte von Luft mit der Flughöhe, oder die Masse eines Flugzeuges mit der Zeit. In der adaptiven Regelung werden die Reglerparameter automatisch den sich ändernden Bedingungen angepasst. Adaptive Regelungen können u.a. durch flexible Regleralgorithmen (Controller Switching Technology) realisiert werden. Flexible Regleralgorithmen ermöglichen es, unterschiedliche, an den jeweiligen Arbeitspunkt angepasste, Reglerstrukturen und Reglerparameter im laufenden Betrieb umzuschalten. Dafür muss je Arbeitspunkt ein Trigger-Signal oder eine Signalspanne definiert werden, welche eindeutig die anzuwendende Reglerstruktur und Reglerparameter bestimmt. Kleinere Abweichungen der Regelstrecke vom Entwurfsmodell werden mittels Methoden zur Robusten Regelung abgedeckt.

Die prädiktive Regelung beinhaltet eine spezielle Komponente (den Prädiktor) zur Vorhersage des künftigen Systemverhaltens.^[23] Die Vorhersage ermöglicht eine verbesserte Ermittlung des Stellwertes in Bezug auf das gewünschte künftige Verhalten. Klassische Regler ohne Prädiktor müssen die Reaktion der Regelstrecke auf den Stellwert abwarten, können also nur reagieren. Die Prädiktive Regelung bezeichnet diesen allgemeinen Ansatz, wobei unterschiedliche spezifische Realisierungen existieren (Smith-Prädiktor, Internal Model Control, Model Predictive Control). Prädiktive Regelungsstrukturen sind besonders vorteilhaft, wenn die Strecke stark verzögerndes Verhalten aufweist, etwa große Totzeiten.

In der Fuzzy Regelung werden den Signalen (Regelgröße, Regelfehler, Stellwert) symbolische Werte anstatt numerischer Werte zugewiesen.^[23][27] Dieses Vorgehen ist besonders vorteilhaft, wenn intuitives Expertenwissen über die manuelle Regelung des Prozesses vorhanden ist, ein formaler Reglerentwurf wegen eines fehlenden Modells jedoch nicht praktikabel ist. Die Fuzzy Regelung basiert auf der Fuzzy-Logik, die eine Erweiterung der booleschen Logik ist. Die Fuzzy Regelung wurde erstmals zur Steuerung der U-Bahn in Sendai in der Praxis erfolgreich eingesetzt (siehe U-Bahn Sendai).

Neuronale Netze werden in der Regelungstechnik sowohl zur Darstellung von Kennfeld-Reglern als auch zur Systemidentifikation verwendet.^[28] Beispielsweise können neuronale Netze zum Autotuning von PID-Reglern oder für die adaptive Regelung eingesetzt werden.

Analyse des Kreisverhaltens

Stabilität

Hauptartikel: Stabilitätstheorie

Die Stabilität des Regelkreises ist eine grundlegend wichtige Eigenschaft, da in der Praxis Instabilität meist zu Schäden führt (z. B. Absturz eines Flugzeuges, Explosion eines Kessels usw.). Grundlegende Erkenntnisse zur Stabilitätstheorie wurden von Maxwell, Routh und Hurwitz beigetragen.

Zur Beurteilung der Stabilität eines Regelkreises existieren mehrere Stabilitätsbegriffe und dazugehörige Analysemethoden, welche die Stabilitätstheorie bilden. Grundvoraussetzung für die Stabilitätsprüfung ist, dass ein mathematisches Modell der Regelstrecke vorliegt.

Gängige Stabilitätsbegriffe sind die Zustandsstabilität und Eingangs-/Ausgangs-Stabilität (E/A-Stabilität). Die Zustandsstabilität fordert anschaulich, dass alle Zustandsvariablen ohne äußeren Einfluss auf ein Gleichgewicht zustreben. Bei LZI-Systemen ist dies der Ursprung, bei nichtlinearen Systemen kann es mehrere Gleichgewichtszustände geben. Zu ihrer Analyse ist die Eigenbewegung des Systems maßgeblich. Die E/A-Stabilität (auch BIBO-Stabilität, engl. bounded input-bounded output) fordert lediglich, dass die Ausgangssignale bei beschränkten Eingangssignalen und verschwindendem Anfangszustand beschränkt bleiben.

Im Fall von LZI-Systemen kann für die Betrachtung der Stabilität auf die charakteristische Gleichung zurückgegriffen werden, welche das charakteristische Polynom verwendet. Liegen bei zeitkontinuierlichen Systemen alle Eigenwerte, das heißt Lösungen der charakteristischen Gleichung, in der linken Halbebene der komplexen s-Ebene, so ist der Regelkreis stabil. Weitere Kriterien zur Prüfung der Stabilitätseigenschaft für LZI-Systeme sind das Hurwitzkriterium, das Phasenrandkriterium und das Nyquistkriterium.

Ein sehr allgemeines, auch für nichtlineare Systeme geeignetes Kriterium zur Stabilitätsprüfung ist die direkte Methode von Ljapunov anhand der Ljapunov-Funktion (Ljapunov-Methode). Weitere für nichtlineare Systeme anwendbare Stabilitätskriterien sind das Popov-Kriterium^[23][29] und das Kreiskriterium.^[23][30]

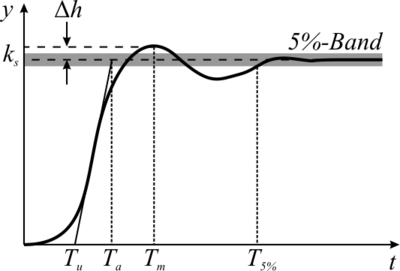Kenngrößen des Verhaltens eines dynamischen Systems, dargestellt anhand der Sprungantwort. Die Verzugszeit T_u und Anstiegszeit T_a sind durch die Wendetangente bestimmt. Die Überschwingzeit T_m ist durch den Zeitpunkt, an dem das erste Maximum der Sprungantwort auftritt, festgelegt. Die Beruhigungszeit T_5% ist der letzte Zeitpunkt, zu dem die Sprungantwort in ein Band der Breite ±5% eintaucht.

Sollwertfolge

Die Sollwertfolge kann anhand der Übertragungsfunktion des geschlossenen Kreises überprüft werden. Die Frequenz Null muss mit der Verstärkung eins übertragen werden, dann ist Sollwertfolge gewährleistet.

Dynamisches Übergangsverhalten

Unter dem dynamischen Übergangsverhalten werden Anforderungen an das Kreisverhalten zusammengefasst, die seine Geschwindigkeit und sein Überschwingen betreffen (siehe Abbildungen). Sie werden anhand der Übergangsfunktion definiert. Die Überschwingzeit T_m bezeichnet den Zeitpunkt des ersten Überschwingmaximums der Sprungantwort. Die Zeit T_5% bezeichnet die Zeit, nach der die Sprungantwort ein Band der Breite ±5% nicht mehr verlässt. Die Überschwingweite bezeichnet die Amplitude der Schwingung einer Sprungantwort um den statischen Endwert. Weitere Kenngrößen sind die Verzugszeit T_u und die Anstiegszeit T_a.

Weitere gebräuchliche Maße für die Güte des Regelverhaltens sind Integralkriterien, die geeignet sind, die Güte des Regelverhaltens in Abhängigkeit von den durch die Sprungantwort und die Führungsgröße abgegrenzten Flächen abzuschätzen. Ein solches Gütekriterium ist das ITAE-Kriterium.

Realisierung von Regelungen

Hauptartikel: Regler

Regler im Produktionseinsatz

Kompaktregler

Zur Realisierung eines Regelkreises muss der entworfene Regler physikalisch realisiert werden. Hierzu können Analogrechner, digitale Kompaktregler oder Soft-Regler in einer geeigneten Speicherprogrammierbaren Steuerung eingesetzt werden. Siehe auch Artikel Regler, sowie.^[31][32][33]

Je nach Aufbau und Einsatzzweck lassen sich unterscheiden:

• Industrieregler → maschinennahe Einzelregler für Kleinanlagen mit eigenem Mikroprozessor
• Prozessregelgeräte → erweiterbare Industrieregler mit Schnittstelle zu übergelagertem (Leit-)System
• Universalregler → Prozessregler in Form von Erweiterungskarten oder Software-Regelbausteinen für programmierbare Steuerungen
• Branchenregler → Spezielle Prozessregler, die für bestimmte Anwendungsgebiete optimiert sind.

Rapid-Prototyping in Forschung und Entwicklung

In der Forschung und Entwicklung entsteht regelmäßig das Problem, neue Regelungskonzepte zu testen. Die wichtigsten Software-Werkzeuge für rechnergestützte Analyse, Entwurf und Rapid Control Prototyping von Regelungen sind nachfolgend aufgeführt.

• MATLAB und Simulink, The MathWorks: Durch zahlreiche Toolboxes ein sehr umfangreiches Softwarepaket für numerische Mathematik, für Simulation, Systemidentifikation, Reglerentwurf und Rapid Control Prototyping geeignet (kommerziell)
• Scilab, Institut National de Recherche en Informatique et en Automatique (INRIA): Ebenfalls sehr umfangreiches Softwarepaket für numerische Mathematik mit ähnlichem Konzept und ähnlicher Syntax wie MATLAB, für Simulation, Systemidentifikation und Rapid Control Prototyping geeignet (frei)
• CAMeL-View TestRig: Entwicklungsumgebung zur Modellbildung von physikalischen Systemen mit dem Schwerpunkt Reglerentwurf und Rapid Control Prototyping sowie zur Anbindung an Versuchsstände (kommerziell)
• Maple: Computeralgebra-System, beherrscht numerische und symbolische Mathematik, besonders für manche Entwurfsverfahren der nichtlinearen Regelung geeignet (kommerziell)
• Mathematica, Wolfram Research, Inc.: Umfangreiches Softwarepaket für numerische und symbolische Mathematik (kommerziell)
• dSPACE: Integrierte Hard- und Software-Lösungen für die Anbindung von MATLAB an Versuchsstände (kommerziell)
• LabVIEW, National Instruments (NI): Integrierte Hard- und Software-Lösungen für die Rechnersteuerung von Versuchsständen (kommerziell)
• ExpertControl: Software-Lösungen für vollautomatische Systemidentifikation und vollautomatische, modellbasierte Reglerauslegung für klassische Reglerstrukturen (PID-Regler) sowie Reglerstrukturen für Systeme höherer Ordnung (kommerziell)
• TPT: Systematisches Testwerkzeug für Regelungssysteme, das neben der Simulation auch eine Ergebnisauswertung und Analysemöglichkeit bietet.
• SCALE-RT: Skalierbare Open-Source und Linux-basierte Echtzeit-Simulationssoftware SCALE-RT bietet eine Echtzeitsimulations-Umgebung für SiL und HiL-Simulationen auf kommerzieller PC-Hardware. (kommerziell)

Alle aufgeführten Werkzeuge zeigen ein hohes Maß an Flexibilität bezüglich der Anwendung und der verwendbaren Reglerstrukturen.

Anwendungen und Beispiele

Häufige Regelungsprobleme

Nachfolgende Auflistung nennt unabhängig von konkreten Anwendungen einige physikalische bzw. chemische Größen, die typischerweise als Regelgrößen auftreten. Auf konkrete Anwendungen wird im nächsten Abschnitt eingegangen.

• Temperaturregelung
• Druck- und Kraftregelung
• Durchfluss- und Mengenregelung
• Füllstandsregelung
• Lage-, Positions-, und Entfernungsregelung
• Geschwindigkeits- und Beschleunigungsregelung
• Drehzahl- und Drehmomentregelung
• Regelung chemischer Größen, wie Konzentrationen, in der Verfahrenstechnik

Technische Anwendungen

Transrapid

Verbrennungsmotor

Talsperre

• Bahntechnik: In der Antriebsregelung treten vielfältige Regelungsprobleme auf, es sind beispielsweise Drehmoment und Geschwindigkeit zu regeln. An der U-Bahn Sendai wurde die Fuzzy-Regelung erfolgreich eingesetzt.
• Luftfahrt: Regelungsprobleme treten in zahlreichen Komponenten von Flugzeugen auf, etwa in den Turbinen, aber auch bezogen auf die Flugdynamik. Beispiele für flugdynamische Regelungsprobleme sind die Kontrolle der Roll-, Gier-, und Nickwinkel, sowie der Autopilot. Siehe auch Flugsteuerung.
• Energietechnik: Stellungsregelung eines Stellventils mit Stellantrieb innerhalb einer Reglerkaskade. In Elektroenergienetzen sind Spannung und Frequenz netzweit zu halten. In jedem Kraftwerk werden Spannung und Frequenz lokal geregelt, so dass die Aufgabe mit dezentralen Reglern durch Variation der Regelleistung gelöst wird (siehe auch Kraftwerksmanagement). Global werden lediglich die Leistungssollwerte der einzelnen Kraftwerke vorgegeben. Die Drehzahlregelung einer Dampfmaschine mit Fliehkraftregelung ist ein klassischer Anwendungsfall
• Kraftfahrzeugtechnik: Tempomat und Antiblockiersystem (ABS), aber auch elektronisches Stabilitätsprogramm sind bekannte Regelungen im Fahrzeugbereich, die auch als Fahrerassistenzsysteme bezeichnet werden. Auch Verbrennungsmotoren beinhalten vielfältige Regelkreise, beispielsweise für Leerlaufdrehzahl, Luftverhältnis (siehe auch Lambdasonde), Klopfregelung (siehe auch Klopfen (Verbrennungsmotor)). Moderne automatische Schaltgetriebe benötigen ebenfalls Regelkreise für die Synchronisation beim Schalten.
• Pipeline: In Pipelines kommen vor allem vermaschte Regelungen vor, für Durchfluss, Druckregelung (Vordruck, Nachdruck) und Stellungsregelung einschließlich Grenzwertregelung.
• Robotik: In der Fertigungsautomatisierung sind die Achsen der Fertigungsroboter zu positionieren. Hier spielen eine schnelle Beruhigungszeit und geringstes Überschwingen eine besonders große Rolle.
• Verfahrenstechnik: In verfahrenstechnischen Prozessen treten Regelungsprobleme für jegliche chemische und physikalische Größen auf, die im betrachteten Prozess eine Rolle spielen. Beispiele sind die Regelung von Füllstand, Temperatur, pH-Wert und Sauerstoffgehalt eines Rührkessel-Reaktors oder das konstant halten von Stoff- bzw. Ionenkonzentrationen mit einem Chemostat.
• Wasserwirtschaft: Zur Vermeidung von Überschwemmungen und Sicherung der Wasserversorgung sind unterlagerte Regelungen von Ketten von Talsperren bedeutsam. Der Füllstand eines einzelnen Stausees wird von einem übergeordneten Management vorgegeben und lokal geregelt.

Berufsverbände mit Bezug zur Regelungstechnik

Deutschland

• Gesellschaft Mess- und Automatisierungstechnik (GMA) des VDI/VDE

International

• International Federation of Automatic Control (IFAC)
• Institute of Electrical and Electronics Engineers (IEEE)

Siehe auch

•  Portal:Mess-, Steuerungs- und Regelungstechnik – Übersicht zu Wikipedia-Inhalten zum Thema Mess-, Steuerungs- und Regelungstechnik
• Steuerungstechnik
• Control in the Field
• Elektrotechnik
• Mechatronik

Literatur

• Otto Föllinger: Regelungstechnik. Hüthig Verlag, ISBN 3-7785-2336-8.
• Martin Horn, Nicolaos Dourdoumas: Regelungstechnik. Pearson Studium, 2006, ISBN 3-8273-7260-7.
• Rolf Isermann: Identifikation dynamischer Systeme. Band 1 und 2, Springer Verlag, 1992, ISBN 3-540-55468-8.
• Lennart Ljung: System Identification - Theory for the User. Prentice Hall, ISBN 0-13-656695-2.
• Jan Lunze: Regelungstechnik 1. 6 Auflage. Springer Verlag, Berlin 2007, ISBN 978-3-540-70790-5. Regelungstechnik 2. 4 Auflage. Springer Verlag, Berlin 2006, ISBN 978-3-540-32335-8.
• Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink. 8. Auflage. Verlag Harri Deutsch, 2010, ISBN 978-3-8171-1859-5.
• Heinz Mann, Horst Schiffelgen, Rainer Froriep,: Einführung in die Regelungstechnik. Carl Hanser Verlag, München 2005, ISBN 978-3-446-41765-6.
• Kurt Reinschke: Lineare Steuerungs- und Regelungstheorie. Springer Verlag, Dresden 2005, ISBN 3-540-21886-6.
• Gerd Schulz: Regelungstechnik. Oldenbourg Verlag, 2002, ISBN 3-486-25858-3.
• Heinz Unbehauen: Regelungstechnik. 1, Vieweg, Braunschweig 2005, ISBN 3-528-93332-1. Regelungstechnik. 2, Vieweg, Braunschweig 2000, ISBN 3-528-73348-9.
• Josef Uphaus: Regelungstechnik. Bildungsverlag Eins, 2005, ISBN 3-427-44510-0.
• samson.de (Hrsg.): Begriffe und Symbole der Regelungstechnik. (pdf).
• Jürgen Adamy: Nichtlineare Regelungen. Springer Verlag, Berlin 2009, ISBN 978-3-642-70793-1.

Zeitschriften und Journale:

• VDI/VDE-GMA, NAMUR (Interessengemeinschaft Prozessleittechnik der chemischen und pharmazeutischen Industrie) (Hrsg.): at – Automatisierungstechnik. 1953ff (monatlich, at-technik.de). atp – Automatisierungstechnische Praxis. München, ISSN 0178-2320. atpi – Automation Technology in Practice. Oldenbourg Wissenschaftsverlag (weblink).
• MSR-Magazin. Zeitschrift für Messen, Steuern, Regeln. Verlag für Technik & Wirtschaft VTW (industrie-service.de, VTW).
• International Journal of Control. Taylor & Francis (tandf.co.uk).
• IFAC (Hrsg.): Automatica. Elsevier (elsevier.com).
• European Journal of Control. hermes Science (elet.polimi.it, editions-hermes.fr).
• Institution of Engineering and Technology (IET) (Hrsg.): IEE Proceedings - Control Theory & Applications. (ietdl.org, IET: theiet.org).
• Norwegian Society of Automatic Control (Hrsg.): Modeling, Identification and Control. (itk.ntnu.no, nfaplassen.no).
• Wroclaw University of Technology (Hrsg.): Systems Science. (Wroclaw UT).
• IEEE Control Systems Society (CSS) (Hrsg.): IEEE Control Systems Magazine. (web). IEEE Transactions on Automatic Control. (web). IEEE Transactions on Control Systems Technology. (web, ieeecss.org).
• ASME American Society Of Mechanical Engineers (Hrsg.): Journal of Dynamic Systems, Measurement, and Control. (scitation.aip.org, asme.org).

Weblinks

 Commons: Regelungs- und Steuerungstechnik (Control engineering) – Sammlung von Bildern, Videos und Audiodateien

Deutschland

• Regelungstechnische Institute in Deutschland
• RoboterNetz Regelungstechnik

Einzelnachweise

1. ↑ Wasseruhr des Ktesibios (Rekonstruktion)
2. ↑ Wasseruhr des Ktesibios (Rekonstruktion), [1], Seite 26
3. ↑ Temperaturregelung in einem Brutkasten, [2], Seite 27
4. ↑ ^{a b c d} Günter Ludyk: Theoretische Regelungstechnik, Springer 1995, Band 1, Seite 1
5. ↑ H. Nyquist: Regeneration theory, Bell Syst. techn. Journ.11, 1932, Seiten 126 bis 147
6. ↑ R. W. Evans: Graphical Analysis of Control Systems, Transactions AIEE 67 (1948), Seiten 547 - 551
7. ↑ Otto Föllinger: Regelungstechnik, Hüthig Verlag, Seite 200, ISBN 3-7785-2336-8
8. ↑ R. On the Generel Theory of Control Systems, Proceedings 1st International Congress on Automatic Control 1960, Butterworths, London, 1961, band 1, Seiten 481 - 492
9. ↑ Heinz Töpfer und Hans-Joachim Zander: Steuerungstechnik - ein Teilgebiet der Automatisierungstechnik, ein Rückblick auf diesbezügliche Forschungsarbeiten in der DDR, Automatisierungstechnik, 2003, Heft 3, Seite 136, 2.1, zweiter Absatz
10. ↑ Otto Föllinger: Regelungstechnik, Hüthig Verlag, Seiten 12 bis 14, ISBN 3-7785-2336-8
11. ↑ In der theoretischen Regelungstechnik wird Übertragungsfunktion auch für Frequenzgang gebraucht. Zudem ist eine Verwechslung mit Übergangsfunktion möglich. Im vorliegenden Artikel werden Übertragungsfunktion, Übertragung und Übertragungs-Glied als allgemeingültige Begriffe, die keiner formalen Einschränkung unterliegen, gebraucht.
12. ↑ In der theoretischen Regelungstechnik wird die Antwort auf die Eingangs-Sprungfunktion auch Übergangsfunktion genannt.
13. ↑ Otto Föllinger: Regelungstechnik, Hüthig Verlag, Seite 10, ISBN 3-7785-2336-8
14. ↑ Stuart Benett: A Brief History of Automatic Control, IEEE Control Systems,June 1966, Seite20
15. ↑ Jan Lunze: Regelungstechnik 1. Springer Verlag, 2007, ISBN 3-540-70790-5, Seite 477
16. ↑ Jan Lunze: Regelungstechnik 1. Springer Verlag, 2007, ISBN 3-540-70790-5, Seite 403
17. ↑ Otto Föllinger: Regelungstechnik, Hüthig Verlag, ISBN 3-7785-2336-8, Seiten 201 und 329
18. ↑ Jan Lunze: Regelungstechnik 1. Springer Verlag, 2007, ISBN 3-540-70790-5, Seite 462
19. ↑ Otto Föllinger: Regelungstechnik, Hüthig Verlag, ISBN 3-7785-2336-8, Seite 201
20. ↑ ^{a b} Otto Föllinger, Regelungstechnik, 8. Aufl. 13.3.3
21. ↑ Otto Föllinger, Regelungstechnik, 8. Aufl. 13.5
22. ↑ Otto Föllinger: Nichtlineare Regelungen II. Oldenbourg Verlag, 1980, ISBN 3-486-33253-8, Kap. 4
23. ↑ ^{a b c d e f} Jürgen Adamy: Nichtlineare Regelungen. Springer, 2009, ISBN 978-3-642-00793-4
24. ↑ Otto Föllinger: Nichtlineare Regelungen II. Oldenbourg Verlag, 1980, ISBN 3-486-33253-8, Kap. 7
25. ↑ Rudolph, Joachim: Beiträge zur flachheitsbasierten Folgeregelung linearer und nichtlinearer Systeme endlicher und unendlicher Dimension. Shaker Verlag, Aachen 2003. ISBN 3-8322-1765-7
26. ↑ M. Fliess, J. L. Lévine, P. Martin and P. Rouchon: Flatness and defect of non-linear systems: introductory theory and examples. International Journal of Control 61(6), pp. 1327-1361, 1995
27. ↑ Lefteri H. Tsoukalas, Robert E. Uhrig: Fuzzy and Neural Approaches in Engineering. Wiley-Interscience, 1997, ISBN 0-471-16003-2, Kap. 6
28. ↑ Lefteri H. Tsoukalas, Robert E. Uhrig: Fuzzy and Neural Approaches in Engineering. Wiley-Interscience, 1997, ISBN 0-471-16003-2, Kap. 10
29. ↑ Otto Föllinger: Nichtlineare Regelungen II. Oldenbourg Verlag, 1980, ISBN 3-486-33253-8, Kap. 5.2
30. ↑ Otto Föllinger: Nichtlineare Regelungen II. Oldenbourg Verlag, 1980, ISBN 3-486-33253-8, Kap. 5.8
31. ↑ Jürgen Müller: Regeln mit SIMATIC. Publicis Corporate Publishing, Erlangen 2004, ISBN 3-89578-248-3
32. ↑ Manfred Schleicher: Regelungstechnik für den Praktiker. Fa. JUMO GmbH & Co, 2006, ISBN 3-935742-00-2
33. ↑ Berthold Heinrich [Hrsg.]: Messen, Steuern, Regeln. Vieweg Verlag, Wiesbaden 2005, ISBN 3-8348-0006-6