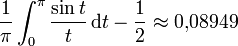Überschwinger

Gibbssches Phänomen bei einer Rechteckskurve

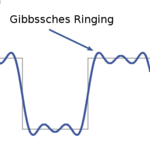
Als Gibbssches Phänomen oder „Ringing“ bezeichnet man in der Mathematik das typische Verhalten von Fourierreihen in der Umgebung von Sprungsstellen. Entwickelt man eine Fourierreihe aus einer unstetigen Funktion, so ergeben sich an den Unstetigkeitsstellen typische Über- und Unterschwinger, die sich auch dann nicht verringern, wenn man versucht, die Funktion durch weitere Summenglieder zu approximieren.

Die relative Höhe des Überschwingers in einer Richtung, bezogen auf die halbe Sprunghöhe, lässt im Grenzwert unendlich vieler Fourier-Summenglieder bestimmen zu:

$\frac{1}{\pi}\int_0^\pi \frac{\sin t}{t}\, \mathrm dt - \frac{1}{2} \approx 0{,}08949$

womit sich ein prozentueller Fehler von etwa 18% der Sprunghöhe ergibt.

Der Effekt wurde nach seinem Entdecker, dem amerikanischen Physiker Josiah Willard Gibbs, benannt.

Ringing in der Datenkompression

In der Praxis bedeutet das etwa für die Bildkompression, dass sich ein Bild, das harte Farbübergänge aufweist (wie etwa bei Text, Strichzeichnungen oder einfachen Diagrammen), nur sehr schlecht mit verlustbehafteten Verfahren wie JPEG komprimieren lässt. Um ein derartiges Bild ohne sichtbare Ringing-Artefakte zu komprimieren, wäre eine sehr hohe Qualitätsstufe notwendig, was zu einer wesentlich größeren Datei als bei verlustfreier Komprimierung führen würde. Es wird daher empfohlen, für derartige Bilder verlustfreie Grafikformate wie PNG zu verwenden.

Ein hochfrequentes Bild Dateigröße mit PNG: 1007 Byte

Das gleiche Bild JPEG-komprimiert; es entstehen Ringing-Artefakte Dateigröße: 4273 Byte

Vergrößerung des JPEG-komprimierten Bildes

Die Ringing-Artefakte lassen sich durch bestimmte Grafikfilter, etwa den Lanczos-Filter, teilweise reduzieren. Diese Methode, manchmal „Deringing'“ genannt, wird bei einigen neueren Video-Decodern eingesetzt.

Weitere Verwendung des Begriffs „Ringing“

Das Gibbsche Phänomen sollte nicht mit dem Überschwingen von Signalen verwechselt werden.

„Ringing“ (deutsch „Ringbildung“) ist der englische Ausdruck für die unerwünschte Schwingneigung oder für unexakte Schaltzustands-Übergänge in elektronischen Schaltungen.

Weblinks

• Mathworld: Gibbs phenomenon