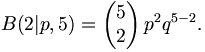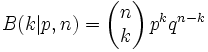Bernoulli-Experiment

Ein Bernoulli-Prozess ist ein zeitlich diskreter stochastischer Prozess, der aus einer endlichen oder abzählbar-unendlichen Folge von unabhängigen Versuchen mit Bernoulli-Verteilung besteht, d.h., für jeden der Zeitpunkte 1, 2, 3, ... wird "ausgewürfelt", ob ein Ereignis mit Wahrscheinlichkeit p eintritt oder nicht.

Beispiel (p = 1 / 3; das Symbol ♦ steht für "Ereignis tritt ein", ◊ für "Ereignis tritt nicht ein"):

◊-♦-◊-♦-◊-◊-♦-◊-♦-◊-♦-◊-◊-◊-◊-◊-♦-◊-◊-◊-◊-◊-◊-◊-♦-◊-◊-◊-◊-◊-♦-◊-♦-◊-♦-◊-◊-◊-♦-♦-◊-♦-♦-◊-◊-◊-◊-♦-◊-♦ ...

Der Prozess kann durch eine Folge von Zufallsvariablen X₁, X₂, X₃,..., beschrieben werden, deren jede mit der konstanten Wahrscheinlichkeit p den Wert X = 1 (Erfolg) und mit der Wahrscheinlichkeit q = 1 − p den Wert X = 0 (Misserfolg) annimmt. Je nach Fragestellung interessiert man sich für eine oder mehrere der folgenden Zufallsvariablen:

• Die Anzahl k erfolgreicher Versuche nach Durchführung von insgesamt n Versuchen; sie folgt einer Binomialverteilung.
• Die Anzahl n von Versuchen, die benötigt werden, um eine vorgegebene Anzahl von r Erfolgen zu erzielen; sie folgt der negativen Binomialverteilung.

Beispiele:

• Ein betrunkener Fußgänger (oder ein diffundierendes Teilchen) bewegt sich bei jedem Schritt mit der Wahrscheinlichkeit p vorwärts, mit der Wahrscheinlichkeit q rückwärts. Man interessiert sich für die Entfernung vom Ausgangspunkt 2k − n. Ein solches Modell wird in der Physik als eindimensionale Zufallsbewegung (Random Walk) bezeichnet.

Eigenschaften:

• Ein Bernoulli-Prozess ist eine spezielle Markow-Kette: beim "Zeitschritt" von n nach n + 1 geht das System mit der Wahrscheinlichkeit p aus dem "Zustand" k in den Zustand k + 1 über; sonst bleibt es im Zustand k.

Die Zufallsvariable k, die angibt, wie viele von n Bernoulli-Versuchen erfolgreich waren, folgt der Binomialverteilung. Wir leiten diese Verteilung anhand eines Beispiels her:

Beim Würfeln werde die Sechs als Erfolg gewertet; die Erfolgswahrscheinlichkeit ist also p = 1 / 6, die komplementäre Misserfolgswahrscheinlichkeit q = 5 / 6. Gefragt sei nun nach der Wahrscheinlichkeit, in n = 5 Würfen genau k = 2 Sechsen zu werfen.

Antwort: Die Wahrscheinlichkeit, erst zwei Sechsen, dann drei Nicht-Sechsen zu werfen, ist p²q³. Da es auf die Reihenfolge aber nicht ankommt, ist diese Wahrscheinlichkeit zu multiplizieren mit der Anzahl der Möglichkeiten, zwei (ununterscheidbare) Sechserwürfe auf fünf Würfe zu verteilen. Der Kombinatorik zufolge ist diese Anzahl durch den Binomialkoeffizienten "5 über 2" gegeben; die gesuchte Wahrscheinlichkeit lautet also:

$B(2 |p,5) = \left( \begin{matrix} 5\\ 2 \end{matrix} \right) p^2 q^{5-2} .$

Davon verallgemeinert, lautet die Wahrscheinlichkeit, in n Bernoulli-Versuchen genau k mal Erfolg zu haben,

$B(k|p,n) = \left( \begin{matrix} n\\ k \end{matrix} \right) p^k q^{n-k}$

mit q = 1 − p. Diese Funktion heißt Binomialverteilung oder binomische Verteilung.