Beschäftigter Biber

Fleißige Biber (auch engl. Busy Beaver) sind Turingmaschinen, die möglichst viele Einsen auf das Band schreiben, ohne in eine Endlosschleife zu geraten (d. h. die nach einer endlichen Anzahl Rechenschritte halten). Die Radó-Funktion (auch Fleißiger-Biber-Funktion) gibt die maximale Anzahl der Einsen an, die ein fleißiger Biber mit einer gegebenen Anzahl von Zuständen schreiben kann. Beides wurde erstmals 1962 vom ungarischen Mathematiker Tibor Radó betrachtet.

Formelle Betrachtung

Definition

Ein Fleißiger Biber ist die Turingmaschine mit dem zweielementigen Alphabet {0,1} und n Zuständen, die hält und zuvor auf ein leeres (aus Nullen bestehendes) Band die maximale Anzahl k_n von Einsen schreibt, verglichen mit allen anderen haltenden Turingmaschinen mit ebenfalls n Zuständen. Nur Turingmaschinen, die nicht halten, können mehr Einsen schreiben.

Fleißiger-Biber-Funktion

Über die Anzahl k_n von Einsen, die ein fleißiger Biber mit n Zuständen schreibt, definiert man den Wert der Fleißiger-Biber-Funktion (auch Radó-Funktion) an der Stelle n: Σ(n) = k_n.

Nicht lösbares Problem

Die Bestimmung der fleißigen Biber ist ein Problem, das nicht allgemein algorithmisch lösbar ist. So ist nicht generell entscheidbar, ob eine gegebene Turingmaschine mit n Zuständen tatsächlich eine Kette von Einsen maximaler Länge schreibt. Für einzelne Turingmaschinen geringer Komplexität ist das allerdings möglich. Also ist die Menge der Werte von Σ(n) weder entscheidbar, noch rekursiv aufzählbar, obwohl Σ(n) wohldefiniert ist. Da auch das Komplement dieser Menge nicht rekursiv aufzählbar ist, wird diese Menge gerne als Beispiel für eine Sprache gewählt, die nicht in der ersten Stufe der arithmetischen Hierarchie liegt.

Wegen dieser Eigenschaften der Wertemenge ist die Funktion Σ nicht berechenbar. Man kann außerdem zeigen, dass ihr asymptotisches Wachstum stärker ist als das jeder berechenbaren Funktion.

Praktische Betrachtung

In der Praxis hat sich gezeigt, dass schon für n > 5 eine Erkenntnis über den Wert Σ(n) realistisch gesehen nicht mehr möglich zu sein scheint. Dazu müsste man für jede einzelne Turingmaschine mit n Zuständen jeweils herausfinden, nach wievielen Schritten sie hält, oder anderenfalls beweisen, dass sie das nicht tut. Aus Gödels Unvollständigkeitssatz folgt direkt, dass nicht für alle solche Turingmaschinen ein entsprechender Beweis existiert. Ob bereits für n = 5 eine solche Erkenntnislücke vorliegt, ist bislang nicht bekannt. Durch die Untersuchung bestimmter Eigenschaften konnten inzwischen zumindest bis auf 40 Maschinen, die kein reguläres Verhalten zeigen^[1], eine Unterteilung in haltende Maschinen, die höchstens 4098 Einsen schreiben und nicht haltenden Maschinen unternommen werden.

Zustände n	Turingmaschinen	Σ(n)
1	144	1 (1962 Rado)
2	104976	4 (1962 Rado)
3	191102976	6 (1965 Lin, Rado)
4	≈ 656,1×109	13 (1972 Weimann, Casper, Fenzel)
5	≈ 3,7×1015	>= 240 (1983 Jochen Ludewig) >= 501 (1983, Uwe Schult) >= 1915 (1984, George Uhing) >= 4098 (1989, Jürgen Buntrock und Heiner Marxen)
6	≈ 30×1018	> 4,64×101439
7	≈ 344×1021	Abschätzung unrealistisch

Ebenfalls nicht berechenbare Funktion

Eine ebenfalls nicht berechenbare Funktion ergibt sich, wenn man die zusätzliche Beschränkung einführt, dass alle Einsen eine zusammenhängende Kette bilden müssen.

Als Bezeichnung dafür hat sich σ(n) eingebürgert.

1965 hat C. Dunham eine äußerst einfache Variante der Funktion des fleißigen Bibers angegeben. D(n) ist definiert als die maximale Anzahl Einsen, die eine Turingmaschine mit zweielementigem Alphabet und n Zuständen schreiben kann, wenn sie auf ein Band mit einem Block von n Einsen angesetzt wird und dabei hält. Wäre diese Funktion berechenbar, so gäbe es auch eine Turingmaschine M mit zweielementigem Alphabet, die 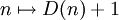$n\mapsto D(n)+1$ berechnet. Diese Turingmaschine habe m Zustände. Dann wäre 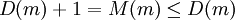$D(m)+1 = M(m) \le D(m)$, wobei das Gleichheitszeichen gerade die Definition von M ist, und das 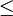$\le$-Zeichen daher rührt, dass M ja eine Maschine mit m Zuständen ist und angesetzt auf m (d.h. auf einen Block aus m Einsen) hält und daher nach Definition von D die Ungleichung 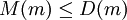$M(m)\le D(m)$ erfüllen muss. Dieser Widerspruch zeigt die Nicht-Berechenbarkeit von D.

Weblinks

• Weitere Informationen
• Seite von Heiner Marxen (englisch)
• Prinzipielle Grenzen der Berechenbarkeit
• Eine Einführung der Uni Stuttgart

Literatur

• J. Ludewig, U. Schult, F. Wankmüller: Chasing the Busy Beaver — Notes and Observations on a competition to find the 5-state Busy Beaver Univ. Dortmund, Abt. Informatik, Bericht Nr. 159, 2. Aufl. 1983.
• A. K. Dewdney: The new Turing Omnibus – 66 Excursions in Computer Science (1993, überarbeitet 1996). Computer Science Press, New York.
• Heiner Marxen und Jürgen Buntrock: Attacking the Busy Beaver 5. Bulletin of the EATCS 40 (Februar 1990), S. 247–251. ISSN 0252-9742.
• F. S. Beckmann: Mathematical Foundation of Programming, Addison-Wesley Publishing Company (1980)
• C. Dunham: A Candidate for the simplest uncomputable function, Communications of the Association for Computing Machinery, Band 8(4), Seite 201 (1965)

Quellen

1. ↑ Busy Beaver nonregular machines for class TM(5)